ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ.
В ходе работы с опытным материалом исследователю приходится проверять те или иные предположения (гипотезы) относительно неизвестных характеристик распределений. Например, он может выдвинуть и проверить гипотезы: "истинное среднее μ равно конкретному числу "μ0=100" или "средние значения двух генеральных совокупностей равны между собой", Кратко эти статистические гипотезы можно обозначить, как Н0 : μ=100, Н0: μ1=μ2.
Конечно, рассматривается не любая научная гипотеза, а лишь статистическая, т.е. утверждение о виде и свойствах распределения, наблюдаемых в эксперименте сл.величин. Гипотеза: на Марсе есть или была жизнь - не статистическая; гипотеза: данная выборка извлечена из нормальной генеральной совокупности - статистическая.
Все три статистические гипотезы, указанное выше, проверяются с помощью того или иного правила, называемого статистическим критерием проверки. При этом, кроме основной проверяемой гипотезы Н0 , выдвигает альтернативную гипотезу Н1 , которую мы примем, если основная гипотеза будет отвергнута.
При одной и той же основной гипотезе H0 альтернативные гипотезы могут быть разными в зависимости от целей исследования, например, возможны задачи:
1) Н0: μ=μ0, Н1: μ 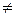 μ0,
μ0,
2) Н0: μ=μ0, Н1: μ<μ0,
3) Н0: μ=μ0, Н1: μ 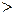 μ0,
μ0,
где μ0 - конкретное число.
В некоторых задачах формулируют лишь основную гипотезу Н0, молчаливо предполагая, что гипотеза Н1 есть просто отрицание Н0.
В ходе проверки гипотезы Н0 можно прийти к правильному решению либо же совершить ошибку первого рода - отклонить H0, когда она верна, а можно совершить ошибку второго рода - принять Н0 , когда она ложна. Вероятности этих ошибок обозначим α и α’ . Это удобно отразить наглядной таблицей.
Два рода ошибок
| Истинная гипотеза | Какое решение принято | Какого рода ошибка | Вероятность ошибки |
| H0 | отвергнуть Н0 | α-уровень значимости | |
| H1 | принять Н0 | α’ |
Желательно провести проверку гипотезы так, чтобы свести к минимуму вероятности α и α’. Это условие не выполнимо при данном объеме выборки. Поэтому задаются малой вероятностью α ошибки 1-го рода, например α=0,05, тогда как вероятность α' явно не контролируется, хотя обеспечивается минимально возможной за счет правильно выбранного критерия. Величину α называют уровнем значимости. Уровень значимости α принято брать 0,05, иногда 0,01. При α=0,05 мы, проверяя на деле истинную гипотезу Н0, будем ее отбрасывать (браковать) с вероятностью 0,05, т.е. в среднем 5 из 100 истинных гипотез H0. Если же риск α ошибки первого рода уменьшить, возрастет риск α' ошибки второго рода. Приняв α=0, мы всегда будем принимать гипотезу Н0 как непротиворечащую опытным данным, независимо от того, верна она или H1. Надо помнить, что данную выборку мы можем получить как при верной, так и при ложной гипотезе Н0 и нельзя принять решение без риска ошибиться.
Дата добавления: 2016-02-27; просмотров: 639;
