Вероятностные характеристики для статистических методов в управлении процессами
Предметом теории вероятности являются только те случайные явления, исходы которых в принципе возможно наблюдать в одних и тех же условиях много раз. Такие случайные явления называют массовыми. Теория вероятностей устанавливает связи между вероятностями случайных событий, которые позволяют вычислять вероятности сложных событий по вероятностям более простых событий (теоремы сложения, умножения и другие).
Как и всякая наука, теория вероятности оперируют рядом основных категорий:
- события;
- вероятность;
- распределение вероятностей.
Событием(ωi)называетсявсякий неразложимый исход случайного эксперимента.
Пространством же элементарных событий (Ω) называется множество всех возможных элементарных событий ωi.
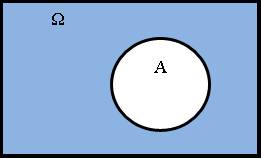
Всякое подмножество А пространства элементарных событий (ПЭС) называют случайным событием. Говорят, что событие А наступило, если наступило хотя бы одно из ωi , входящих в Ω. Иными словами, случайным событием называют такое событие, которое может произойти либо не произойти при соблюдении определенных условий. Само пространство Ω еще называют достоверным событием, имея ввиду событие, которое заведомо произойдет при соблюдении определенных условий. Пустое же подмножество (Ø) множества Ω называется невозможным событием, которое заведомо не произойдет при соблюдении определенных условий.
Говорят, что событие А является причинойсобытия В, если каждое появление события А сопровождается появлением события В, и пишут A ⊂ B. События А и В называют равносильными, если A ⊂ B и B ⊂ A. Равносильность событий обозначается следующим образом A = B. События называются равновозможными, если нет оснований ожидать, что при многократном повторении испытания хотя бы одно из них будет появляться чаще любого другого.
Далее мы будем рассматривать такие испытания, среди возможных исходов которых можно выделить совокупность таких событий, которые образуют Ω. Однако оказывается, что все результаты, которые будут получены для таких испытаний остаются в силе и для тех испытаний, для которых нельзя построить Ω.
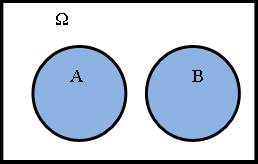
Для наглядности будем использовать представление Ω в виде прямоугольной области на плоскости, а ωi будем изображать точками, лежащими внутри Ω . Случайные события будем изображать в виде фигур.
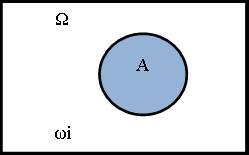
На множестве случайных событий пространства элементарных событий (ПЭС) определены следующие операции: сложение, умножение, вычитание.
1) Суммой событий (А+В) называют событие, состоящее из тех ωi, которые входят либо в А, либо в В, либо в А и В одновременно.
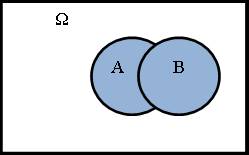
2) Произведением событий A⋅B называют событие, состоящее из тех ωi, которые входят в А и В одновременно.
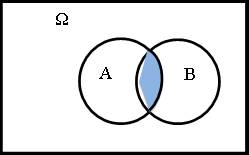
3) Разностью событий (А-В) называют событие, состоящее из тех ωi, которые входят в А, но не входят в В.
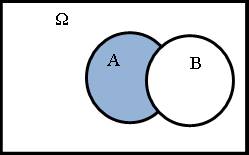
Непосредственно из определений операций над случайными событиями следуют формулы двойственности:
______ ______
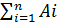 =
= 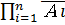 ,
, 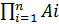 =
= 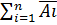
Событие А и В называются несовместимым, если A⋅B = Ø.
Событие 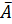 называется противоположным событию А, если А+
называется противоположным событию А, если А+ 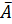 = Ω,
= Ω,
A* 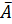 = Ø.
= Ø.
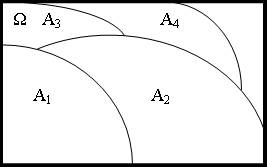
Говорят, что событие A1, A2,…An образуют полную группу событий, если А1+А2+….+Аn = Ω, Аi*Aj = Ø (i неравно j).
Введем понятие предела последовательности событий. Пусть {Аn} будет бесконечной последовательностью случайных событий. Обозначим через А* множество всех тех и только тех элементарных событий, которые принадлежат бесконечному числу множеств Аn. Тогда имеет место формула:
А*= 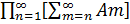 .
.
Действительно, если 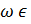 A*, то
A*, то
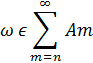
для каждого n, и, следовательно,
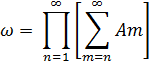
т.е.
А* 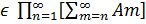 .
.
Если же 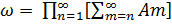 , то
, то 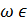 А*, что и требовалось показать.
А*, что и требовалось показать.
Пусть А* - множество тех и только тех элементарных событий, которые принадлежат бесконечному числу множеств Аn, за исключением конечного их числа. Тогда, проводя рассуждения, аналогичные приведенным выше, получаем
А* = 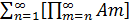 .
.
Очевидно, A* 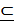 A*. Событие А* называется верхним пределом последовательности
A*. Событие А* называется верхним пределом последовательности 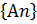
А* = 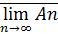 ,
,
а событие А* называется нижним пределом последовательности 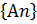
А* = 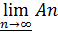 .
.
Если А* = А*, то говорят, что последовательность событий 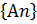 имеет предел
имеет предел
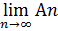 =
= 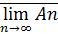 =
= 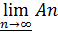 .
.
Операции над событиями помогают упростить вычисление вероятностей сложных случайных событий, выражаемых через другие события с помощью операций сложения, умножения, вычитания и дополнения.
Описанная выше алгебра событий является частным случаем булевой алгебры, в которой в качестве единицы выступает достоверное событие Ω, а в качестве нуля – невозможное событие Ø.
Дополнение булевой алгебры Сx истолковывается как противоположное событие 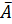 .
.
В качестве булевской операции частичного упорядочения x 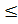 y выступает отношение причинности A ⊂ B, которое имеет место тогда и только тогда, когда A*B = A, так что пространство событий так же является частично упорядоченным.
y выступает отношение причинности A ⊂ B, которое имеет место тогда и только тогда, когда A*B = A, так что пространство событий так же является частично упорядоченным.
Вероятностьявляется одним из основных понятий теории вероятностей. С материалистической философской точки зрения вероятность события – это степень объективной возможности этого события. Иными словами вероятность представляет собой численную характеристику реальности появления того или иного события.
Дадим определение, которое называют классическим.
Если Ω состоит из n равновозможных ωi, то вероятность P(A) события А равна числу m элементарных событий ωi, входящих в А, деленному на число n всех ωi, т.е.
P(A) = 
Таким образом, если множество возможных исходов конечное число, то вероятностью события А считается отношение числа исходов благоприятствующих этому событию к общему числу единственновозможных равновозможных исходов.
Случай равновозможных событий называют классическим. Поэтому и вероятность называется классической. Из определения следует, что 0 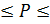 1, вероятность достоверного события P(Ω) = 1, а вероятность невозможного события P(Ø) = 0.
1, вероятность достоверного события P(Ω) = 1, а вероятность невозможного события P(Ø) = 0.
Как правило, вычисление классической вероятности сводится к нахождению чисел m и n методами комбинаторного анализа. Поэтому приведем наиболее употребляемые комбинаторные формулы. В теории вероятностей используют сочетания, размещения, перестановки и принцип умножения.
Пусть дано множество A = {ω1, ω2, …ωn}, состоящее из n элементов.
Сочетанием из n по k называется любое неупорядоченное k – элементное подмножество множества А. Их общее число Nc определяется по формуле
Nc 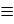
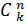 =
= 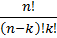 .
.
Размещением из n по k называется любое упорядоченное k – элементное подмножество множества А. Их общее число Nr определяется по формуле
Nr 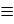
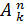 =
= 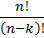 .
.
Перестановка – это размещение при n = k. Их общее число равно
Np 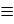
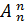 =
= 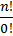 = n!.
= n!.
Принцип умножения. Для упрощения подсчетов классической вероятности часто используется принцип умножения, состоящий в том, что, если требуется выполнить последовательно k действий, то число способов выполнения всех k действий вычисляется по формуле
Nk = n1*n2…*nk,
где n1 – число способов выполнения первого действия, n2 – число способов выполнения второго действия, и т.д.
Пусть k1, k2,….km – целые неотрицательные числа, причем k1+k2+…+km=n. Тогда число способов, которыми можно представить множество А из n элементов в виде суммы m множеств В1, В2,…, Вm, число элементов которых составляет соответственно k1, k2, …km, равно
Nn (k1, k2,…km) = 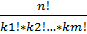 .
.
Числа Nn (k1, k2,…km) называются полиномиальными коэффициентами.
Сочетаниями с повторениями из m элементов по n элементов называются группы, содержащие n элементов, причем каждый элемент принадлежит одной из m типов.
Число сочетаний из m элементов по n элементов с повторениями равно
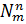 =
= 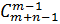 =
= 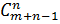 .
.
Ниже рассмотрим пример. Газ, состоящий из n молекул, находится в замкнутом сосуде. Мысленно разделим сосуд на n равных ячеек и будем считать, что вероятность каждой молекулы попасть в каждую из n ячеек одна и та же, и равна  . Какова вероятность того, что молекулы окажутся распределенными так, что в первой ячейке окажутся m1 молекул, во второй m2 молекул и т.д., наконец в n-ой – mn молекул?
. Какова вероятность того, что молекулы окажутся распределенными так, что в первой ячейке окажутся m1 молекул, во второй m2 молекул и т.д., наконец в n-ой – mn молекул?
Решение. Пусть А – событие, состоящее в том, что молекулы окажутся распределенными так, что в первой ячейке окажутся m1 молекул, во второй – m2 молекул и т.д., наконец в n-ой – mn молекул. Требуется найти вероятность Р(А), которая по формуле классической вероятности равна Р(А) =  .
.
В соответствии с принципом умножения n = n1*n2…*nn, где n1 – число способов размещения первой молекулы по n ячейкам, n2 – второй молекулы, …., nn – n-ой молекулы. При этом каждая молекула может находиться в каждой из n ячеек, следовательно, n1 = n2 =…= nn и n молекул можно распределить по n ячейкам nn различными способами. Аналогично подсчитаем число исходов, благоприятствующих событию А,
m = M1*M2…*Mn,
где M1 – число способов размещения m1 – молекул по n ячейкам, M2 – m2 – молекул по (n-m1) ячейкам, ….., Mn – mn – молекул по (n-mn) ячейкам. При этом
M1 = 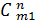 , M2 =
, M2 = 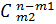 ,…, Mn =
,…, Mn = 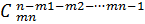 .
.
Тогда окончательно находим
P(A) =  =
= 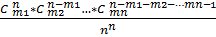 =
= 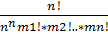 .
.
Распределением вероятностей принято считать законы, описывающие область значений случайной величины и вероятности их принятия.
Прежде чем перейти к законам распределения случайной величины дадим определение дискретной случайной величине.
Случайная величина X называется дискретной, если существует конечная или счетная последовательность чисел y1, y2, y3, …такая, что
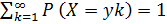 .
.
Среди законов распределения для дискретных случайных величин наиболее распространенным является биномиальный закон распределения.
Биномиальное распределение имеет место в следующих условиях.
Пусть случайная величина 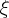 - число появлений некоторого события
- число появлений некоторого события 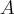 в
в 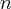 независимых испытаниях, вероятность появления
независимых испытаниях, вероятность появления 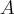 в отдельном испытании равна
в отдельном испытании равна 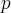 .
.
Данная случайная величина является дискретной случайной величиной, ее возможные значения 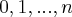 . Вероятность того, что случайная величина
. Вероятность того, что случайная величина 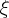 примет значение
примет значение 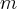 вычисляется по формуле Бернулли:
вычисляется по формуле Бернулли:
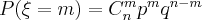 .
.
Закон распределения дискретной случайной величины 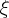 называется биномиальным законом распределения, если вероятности значений случайной величины вычисляются по формуле Бернулли.
называется биномиальным законом распределения, если вероятности значений случайной величины вычисляются по формуле Бернулли.
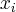
| 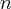
| ||
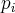
| 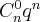
| 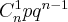
| 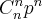
|
Ряд распределения будет иметь вид:
Убедимся, что сумма вероятностей различных значений случайной величины равна 1. Действительно,
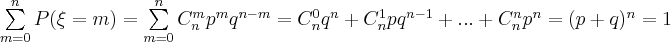
Так как при данных вычислениях получилась биномиальная формула Ньютона, поэтому закон распределения называется биномиальным.
Если случайная величина 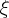 имеет биномиальное распределение, то ее числовые характеристики находятся по формулам:
имеет биномиальное распределение, то ее числовые характеристики находятся по формулам:
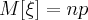
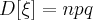
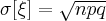
При решении многих практических задач приходится иметь дело с дискретными случайными величинами, которые подчиняются закону распределения Пуассона.
Типичными примерами случайной величины, имеющей распределение Пуассона, являются: число вызовов на телефонной станции за некоторое время 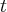 ; число отказов сложной аппаратуры за время
; число отказов сложной аппаратуры за время 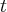 , если известно, что отказы независимы друг от друга и в среднем на
, если известно, что отказы независимы друг от друга и в среднем на
единицу времени приходится 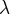 отказов.
отказов.
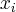
| 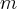
| ||
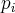
| 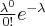
| 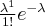
| 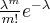
|
Ряд распределения будет иметь вид:
То есть вероятность того, что случайная величина 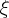 примет значение
примет значение 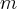 вычисляется по формуле Пуассона:
вычисляется по формуле Пуассона:
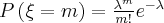
поэтому данный закон и называется законом распределения Пуассона.
Случайная величина, распределенной по закону Пуассона, имеет следующие числовые характеристики:
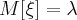
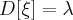
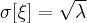
Распределение Пуассона зависит от одного параметра 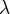 , который является математическим ожиданием случайной величины. Распределение Пуассона может быть использовано как приближенное в тех случаях, когда точным распределением случайной величины является биномиальное распределение, при этом число испытаний велико, а вероятность появления события
, который является математическим ожиданием случайной величины. Распределение Пуассона может быть использовано как приближенное в тех случаях, когда точным распределением случайной величины является биномиальное распределение, при этом число испытаний велико, а вероятность появления события 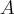 в отдельном испытании мала, поэтому закон распределения
в отдельном испытании мала, поэтому закон распределения
Пуассона называют законом редких событий.
Непрерывная случайная величина 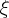 имеет равномерное распределение на отрезке [a;b], если на этом отрезке плотность распределения данной случайной величины постоянна, а вне его равна нулю,
имеет равномерное распределение на отрезке [a;b], если на этом отрезке плотность распределения данной случайной величины постоянна, а вне его равна нулю,
то есть
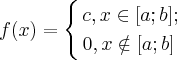
Так как площадь под кривой распределения должна равняться 1, то 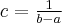 и следовательно, плотность распределения должна иметь вид:
и следовательно, плотность распределения должна иметь вид:
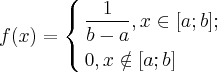
Непрерывная случайная величина 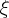 подчиняется закону равномерного распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все
подчиняется закону равномерного распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все
значения случайной величины одинаково вероятны. Случайные величины, имеющие равномерное распределение часто встречаются в измерительной практике при округлении отсчетов измерительных приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является случайной величиной 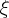 , которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Числовые характеристики случайной величины, имеющей равномерное распределение, вычисляются по формулам:
, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Числовые характеристики случайной величины, имеющей равномерное распределение, вычисляются по формулам:
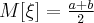
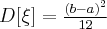
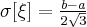
Среди распределений непрерывных случайных величин центральное место занимает нормальный закон распределения.
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
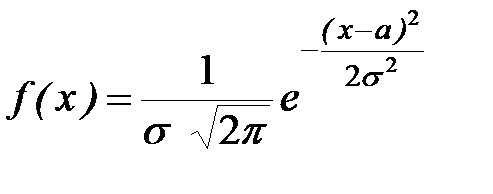 ,
,
где 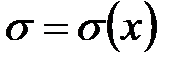 ,
, 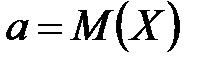
Нормальный закон распределения также называется законом Гаусса. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.
Функция распределения вероятностей для нормального закона имеет вид:
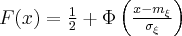
где 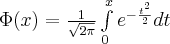 - функция Лапласа.
- функция Лапласа.
Нормальный закон распределения очень широко распространен в задачах практики. Он проявляется во всех тех случаях, когда случайная величина 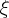 является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину
является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величину 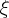 влияет незначительно и нельзя указать, какой именно в большей степени, чем остальные. Примерами случайных величин, имеющих нормальное распределение, могут служить: отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров; ошибки при измерении; отклонения при стрельбе и другие.
влияет незначительно и нельзя указать, какой именно в большей степени, чем остальные. Примерами случайных величин, имеющих нормальное распределение, могут служить: отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров; ошибки при измерении; отклонения при стрельбе и другие.
Основной особенностью, выделяющей нормальный закон среди других законов, служит то, что он является предельным законом для других законов распределения.
Вероятность того, что случайная величина 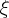 , распределенная по нормальному закону, попадет на промежуток
, распределенная по нормальному закону, попадет на промежуток 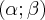 вычисляется по формуле:
вычисляется по формуле:
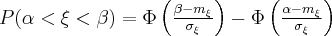
Вероятность того, что случайная величина 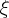 отклонится от своего математического ожидания на величину по модулю меньшую
отклонится от своего математического ожидания на величину по модулю меньшую 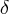 вычисляется по формуле:
вычисляется по формуле:
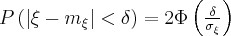
В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, вопросах надежности и других приложениях, часто имеют дело со случайными величинами, имеющими показательное распределение.
Непрерывная случайная величина 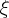 распределена по показательному закону, если ее плотность вероятности имеет вид:
распределена по показательному закону, если ее плотность вероятности имеет вид:
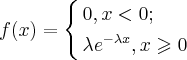
Функция распределения задается следующим образом:
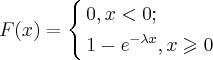
Числовые характеристики случайной величины, имеющей показательное распределение вычисляются по формулам:
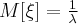
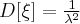
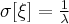
Экспресс-метод расчета на основе широты R. Этот метод основан на использовании для оценки среднего квадратического отклонения широты R как статистической величины, связанной со степенью разброса. Теперь допустим, что из совокупности среднего квадратического отклонения σ сделана выборка для определения среднего ( 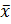 ) и широты (R). Так распределение R принимает вид, показанный на рисунке 2, представляя смещенное, несимметричное распределение, и взаимоотношения между совокупностью и σ оказывается также такими, что и показано на рисунке 2.
) и широты (R). Так распределение R принимает вид, показанный на рисунке 2, представляя смещенное, несимметричное распределение, и взаимоотношения между совокупностью и σ оказывается также такими, что и показано на рисунке 2.
Рис. 2. Распределение R
Значение d2 является в данном случае постоянным, изменяющимся в зависимости от числа n (см. таблицу 2).
Табл. 2 Значение d2, d3
| n | d2 | d3 |
| 1,128 1,693 2,059 2,326 2,534 2,704 | 0,853 0,888 0,880 0,864 0,848 0,833 |
При оценке среднего квадратического отклонения по совокупности на основе широты (R), если число n превышает 10, оценка через R/d2 оказывается менее точной. Это объясняется тем, что при оценке на основе широты предоставляется только информация о существовании данных между наибольшим и наименьшим значениями из n-ного количества единиц данных, а числовые значения между ними игнорируются. Это означает, что чем больше число проб, тем интенсивнее становится утечка информации. Поэтому в случае большого числа проб следует сгруппировать их на 5-10 пакетов данных для определения R, затем на основе 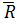 произвести оценку.
произвести оценку.
В качестве типовых вариантов распределения, часто применяемых в контроле качества, можно выделить нормальное распределение, биноминальное распределение и пуассоновское распределение. Нормальное распределение применяется в случае недискретных значений, а биноминальное распределение и пуассоновское распределение – в случае дискретных значений. Ниже попытаемся рассказать о природе распределения.
Распределение недискретных значений:
1. Нормальное распределение. Изобразим гистограмму замеренных значений массы 100 консервных банок, либо же гистограмму замеренных значений толщины листа фанеры. При этом, если увеличить число единиц данных и сделать ширину класса меньше, форма гистограммы становится сходной с колоколообразной, несимметричной, пологой и кривой, достигая пика к центру, и падая к периферии. В быту часто встречается колоколообразное нормальное, или близкое к нормальному, распределение данных, как распределение учеников по массе и росту, распределение ежедневных выручек от реализованный продукции в розничных магазинах, распределение числа пассажиров в автотранспортных компаниях и др. На рисунке 3 приведено нормальное распределение со средним µ и средним квадратическим отклонением σ.
Рис. 3. Нормальное распределение
Таким образом, поскольку для нормального распределения форма распределения определена, вероятность появления данной величины определяется степенью отклонения от среднего. Значит, если нормальное распределение данных разбить на основе среднего квадратического отклонения σ так, как показано на рисунке 4, то в пределы +1 σ от среднего укладывается 68,27% общей частоты по всем данным, в пределы +2 σ – 95,45%, а в пределы + 3 σ – 99,73%. По контрольной карте, о которой речь будет идти далее, вероятность выхода данных за пределы 3 σ составляет порядка 0,3%, поэтому, если произошло то, что происходит три раза на каждые 1000 раз, считают, что распределение изменено, то есть технологический процесс изменился, либо же в технологическом процессе возник какой-либо сбой.
Рис. 4. Нормальное распределение и вероятность
Кроме того, природа нормального распределения применяется также и при установлении стандарта продукции на основе производственной мощности технологического процесса. В этом случае измеряют неоднородность качества изделий, на основе которой определяют среднее квадратическое отклонение, и с помощью 3,5- или 4-кратной величины среднего квадратического отклонения устанавливают стандарт продукции. Так делают потому, что если 3 σ данные выходят за пределы три раза через каждые 1000 раз, то при 3,5,4 σ или 4, 5 σ все данные укладываются в пределы стандарта. Желательно применять 4 σ или 4,5 σ, если это возможно, но в случае, если это будет оказывать большое влияние на выход полезного по расходу сырья, применяется 3,5 σ.
2. Вероятность нормального распределения. Поскольку форма распределения определена, то степенью отклонения от среднего определяется степень появления данной величины (ожидаемое значение степени появления называется вероятностью P). Для общего выражения степени отклонения от центра используется мера U, показывающая, во сколько раз величина отклонения превосходит σ, то есть вероятность появления.
U = 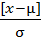
Теперь допустим, что при среднем по совокупности 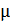 = 50 и среднем квадратическом отклонении по совокупности σ = 2 выбраны данные и произведено измерение, при этом полученный результат составляет 54. Тогда степень отклонения этих данных от центра будет равна 54-50= 4. Если проверить, во сколько раз отклонение данных от центра, больше σ, то, поскольку σ = 2, очевидно, что данные отклонены от центра в два раза больше σ. Из таблицы 3 видно, что вероятность появления данных, отклоняющихся от центра в два раза больше, равна 0,046, то есть 4,6%.
= 50 и среднем квадратическом отклонении по совокупности σ = 2 выбраны данные и произведено измерение, при этом полученный результат составляет 54. Тогда степень отклонения этих данных от центра будет равна 54-50= 4. Если проверить, во сколько раз отклонение данных от центра, больше σ, то, поскольку σ = 2, очевидно, что данные отклонены от центра в два раза больше σ. Из таблицы 3 видно, что вероятность появления данных, отклоняющихся от центра в два раза больше, равна 0,046, то есть 4,6%.
Табл. 3. Мера и вероятность
Это позволяет сделать вывод, что возник очень редкий случай, так как 4,6% меньше 5%. Следовательно, можно заключить, что в технологическом процессе возникло что-то ненормальное, то есть какой-либо сбой. Тем не менее, в такой оценке, вероятность допущения ошибки может составлять 5%. Предположим, что вдруг появилось числовое значение равное 55,2. Тогда степень отклонения данных от центра будет равна 55,2-50 = 5,2. Если проверить, во сколько раз больше отклонены данные от среднего квадратического отклонения, то получается 2,6-кратная величина. Вероятность появления данных, отклоненных в 2,6 раза больше от среднего квадратического отклонения, не превышает 1% (по табл. 3). Поэтому можно сделать вывод, что в технологическом процессе возникла какая-либо неисправность. При этом вероятность допущения ошибки в оценке составляет 1%. Иначе говоря, надежность оценки равна 99%.
3. Распределение средних значений параметров проб. Если определяется среднее 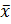 каждой пробы в размере n, выбранной из нормально распределенной совокупности со средним µ и средним квадратичным отклонением σ, то средние значение у этой пробы
каждой пробы в размере n, выбранной из нормально распределенной совокупности со средним µ и средним квадратичным отклонением σ, то средние значение у этой пробы 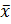 1,
1, 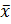 2,
2, 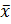 3 оказываются нормально распределенными, причем и разброс средних меньше разброса у исходных проб, и среднее квадратическое отклонение составляет
3 оказываются нормально распределенными, причем и разброс средних меньше разброса у исходных проб, и среднее квадратическое отклонение составляет 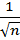 . Однако, общее среднее, как и отдельное среднее, в конечном счете становится равным среднему по совокупности µ. Выражая среднее квадратическое отклонение
. Однако, общее среднее, как и отдельное среднее, в конечном счете становится равным среднему по совокупности µ. Выражая среднее квадратическое отклонение 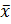 через D (
через D ( 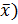 , получим D (
, получим D ( 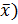 =
= 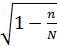 *
* 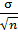
В случае, если N гораздо больше n, 1 -  приближается к 1, поэтому
приближается к 1, поэтому
D ( 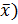 =
= 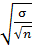 .
.
Порядок определения среднего квадратического отклонения на основе метода распределения средних значений у проб, изложенного в данном пункте, и 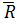 , о котором речь шла ранее, служит основой определения предельной контрольной линии на контрольной карте
, о котором речь шла ранее, служит основой определения предельной контрольной линии на контрольной карте 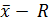 .
.
Рис.5. Распределение средних
4. Аддитивность дисперсии. Теперь допустим, что продукция получается сочетанием двух деталей A и B. Размер x детали A имеет разброс + 4 мм по отношению к проектному размеру. Если размер y детали B имеет разброс + 3 мм, то каков будет разброс длины продукции x+y? Опишем два случая, когда разброс появляется в виде больших групп и спорадически.
В случае, когда разброс появляется в виде больших групп: предположим, что если в какое-то время размер этой продукции непрерывно получается больше проектного, либо же когда он непрерывно получается меньше проектного, то разумнее было бы считать данный разброс + (3+4) = + 7 мм.
В случае, когда разброс появляется спорадически: согласно статистике, разброс размера продукции, получаемой сочетанием деталей, принимается равным 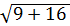 = 5 мм. На практике общепринято считать, что это рационально.
= 5 мм. На практике общепринято считать, что это рационально.
Вышеизложенное основано на принципе аддитивности дисперсии. Когда материал обрабатывается на нескольких технологических стадиях, то обычно разброс размеров постепенно растет по мере перехода с одной стадии на следующую. При обработке отверстий в листовой стали (см. рисунок 6) делают сначала отверстие А1, затем отверстие А2, используя в качестве исходной точки А1, а далее отверстие А3. При этом разброс размеров в зависимости от положения отверстия появляется следующим образом, причем – разброс размеров становится тем больше, чем позднее производится обработка. Так, А1: 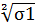 ; А2:
; А2: 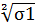 +
+ 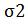 и т.д.
и т.д.
Рис.6. Разброс размера в зависимости от положения
Как излагалось выше, для недискретных (метрических) значений применяется нормальное распределение. Для дискретных же значений, таких как количество брака в штуках, коэффициент брака и др. используется биноминальное распределение, а для числа дефектов текстильных изделий и др. – пуассоновское распределение.
Биноминальное распределение (распределение вероятностей появления брака в штуках). Количество брака в штуках x в пробах размером n, взятых из большой партии с долей брака p от общего количества, подчиняется принципу биноминального распределения.
Табл. 4. Коэффициент брака 10% в случае n = 20
| Количество брака в штуках x в пробах | Вероятность появления брака в количестве x в пробах Px |
| 0,1216 0,2702 0,2852 0,1901 0,0898 0,0319 0,0089 0,0020 0,0004 0,0001 | |
| Итого | 1,0002 |
Распределение, показанное на рисунке 7 называется биноминальным распределением.
Рис .7. Количество брака в штуках в пробах
Природа биноминального распределения. В случае, когда пробы размером n взяты из технологической стадии с коэффициентом брака по совокупности p:
a) Распределение количества брака в штуках pn. Стоит помнить о том, что среднее составляет pn, а среднее квадратическое отклонение рассчитывается как: 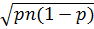 .
.
b) Распределение коэффициентов брака p. Стоит помнить о том, что среднее составляет p, а среднее квадратическое отклонение σ составляет: 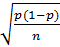 .
.
c) При pn > 5 c биноминальным распределением в принципе можно обращаться как с нормальным распределением.
d) Биноминальное распределение зависит от коэффициента брака по совокупности и размера проб.
Пуассоновское распределение (распределение числа дефектов). Проверяя число раковин (дырок) в окрашенных плитах, полученных на устойчивом технологическом процессе, можно в большинстве случаев проследить статистическое правило (статистическую регулярность), хотя в каждой окрашенной плите в отдельности число раковин варьируется без определенной зависимости (см. табл. 5).
Табл. 5. Распределение числа дефектов в одной
пробе, случайно взятой из совокупности со
предним числом дефектов 3 (Пуассоновское
распределение)
| Число раковин в пробе (x) | Вероятность появления раковин в количестве x в пробе |
| . . . | 0,050 0,150 0,224 0,224 0,168 0,101 0,050 0,022 0,008 0,003 0,001 . . . |
Из таблицы 5 очевидно, что вероятность появления 6 раковин в одной плите равна 5%.
Распределение числа дефектов c в совокупности с числом дефектов c следующее:
Ø среднее составляет с ;
Ø среднее квадратическое отклонение σ составляет 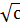 ;
;
Ø в случае числа дефектов в единицу измерения среднее составляет u ;
Ø в случае числа дефектов в единицу измерения среднее квадратическое отклонение составляет 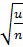 .
.
Контрольная карта c и контрольная карта u для контроля за числом дефектов, о которых речь будет идти далее, основаны на пуассоновском распределении. Распределение, показанное на рисунке 8, называется пуассоновским распределением. Пуассоновское распределение зависит от среднего числа дефектов в совокупности.
Рис. 8.
Дата добавления: 2016-03-22; просмотров: 1288;
