Вероятность гипотез. Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий 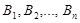, образующих полную группу. Поскольку заранее не из­вестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А опреде­ляется по формуле полной вероятности (см. § 2):

. (*)

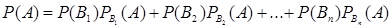Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что собы­тие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

.

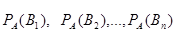Найдем сначала условную вероятность 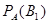. По теореме умножения имеем

.

Отсюда

.

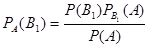Заменив здесь Р(А) по формуле (*), получим

.

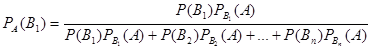Аналогично выводятся формулы, определяющие услов­ные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы 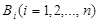может быть вычислена по формуле

.

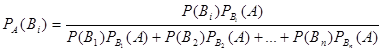Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания в итоге которого появилось событие А.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6,|ко второму - 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым - 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:

1)деталь проверил первый контролер (гипотеза );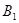

2)деталь проверил второй контролер (гипотеза ).

Искомую вероятность того, что деталь проверил первый контроллер, найдем по формуле Бейеса:

.

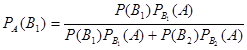По условию задачи имеем:

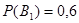(вероятность того, что деталь попадает к первому конт­ролеру);

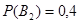(вероятность того, что деталь попадет ко второму конт­ролеру);

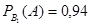(вероятность того, что годная деталь будет признана первым контролером стандартной);

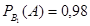(вероятность того, что годная деталь будет признана вторым контролером стандартной).

Искомая вероятность

.

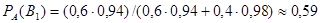Как видно, до испытания вероятность гипотезы 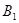равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Бейеса позволило оценить вероятность рассматриваемой гипотезы.

Задачи

1. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым – 0,6. Найти вероятность того, что хотя бы один из стрелков попал м мишень.

Ответ 0,88.

2. У сборщика имеется 16 деталей, наготовленных заводом №1, и 4 детали завода №2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом №1.

Ответ 92/95.

3. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бе­гуна. Вероятность выполнить квалификационную норму такова: для лыжника - 0,9, для велосипедиста - 0,8 и для бегуна - 0,75, Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.

Ответ 0,86.

4. Сборщик получил 3 коробки деталей, наготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода №2 2 – 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.

Ответ 0,84.

5. В первом ящике содержится 20 деталей, из них 15 стандарт­ных; во втором – 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что
наудачу извлеченная деталь из наудачу взятого ящика – стандартная.

Ответ 43/60.

6. В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответст­венно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.

Ответ 0,875.

7. В двух ящиках имеются радиолампы. В первом ящике содер­жится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.

Ответ 13/132.

8. Из полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую извлеченную наудачу кость можно приставить к первой.

Ответ 7/18.

9. Студент знает не все экзаменационные билеты. В каком слу­чае вероятность вытащить неизвестный билет будет для него наимень­шей: когда он берет билет первым или последним?

Ответ Вероятности одинаковы в обоих случаях.

10. В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равноверо­ятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.

Ответ 0,625.

11. При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11, соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?

Ответ Вероятность того, что автомат снабжен сигнализатором С-1, равна 6/11, а С-11—5/11.

12. Для участия в студенческих отборочных спортивных соревновании выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?

Ответ Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59.

13. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрощенная система проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяют стандарту, - с вероятностью 0,05. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту.

Ответ 0,998.