ПОВТОРЕНИЕ ИСПЫТАНИЙ
Формула Бернулли
Если производится несколько испытаний, причём вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.
Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна 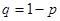 .
.
Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится n-k раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности. Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: 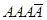 ,
, 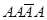 ,
, 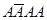 ,
, 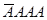 . Запись
. Запись 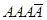 означает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом испытании оно не появилось, т. е. наступило противоположное событие
означает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом испытании оно не появилось, т. е. наступило противоположное событие  соответственный смысл имеют и другие записи.
соответственный смысл имеют и другие записи.
Искомую вероятность обозначим  . Например, символ
. Например, символ 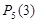 означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
Вывод формулы Бернулли.Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна 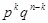 . Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по А элементов, т. е.
. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по А элементов, т. е. 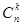 . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:
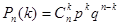
или
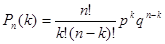 .
.
Полученную формулу называют формулой Бернулли.
Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна b равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна  .
.
Искомая вероятность по формуле Бернулли равна
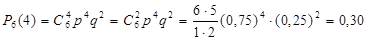 .
.
Дата добавления: 2016-03-27; просмотров: 999;
