Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

Вновь будем считать, что производится n неза­висимых испытании, в каждом из которых вероятность появления события А постоянна и равна р(0<р<1). Поставим перед собой задачу найти вероятность того, отклонение относительной частоты m/n от постоянной вероятности р по абсолютной величине не превышает заданнoгo числа 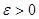. Другими словами, найдем вероятность осуществления неравенства

. (*)

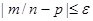Эту вероятность будем обозначать так: 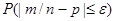. Заменим неравенство (*) ему равносильными:

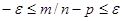или

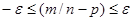
Умножая эти неравенства на положительный множитель 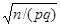, получим неравенства, равносильные исходному:

.

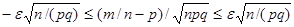Воспользуемся интегральной теоремой Лапласа в форме указанной в замечании (см. § 3). Положив 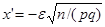и 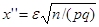, имеем

.

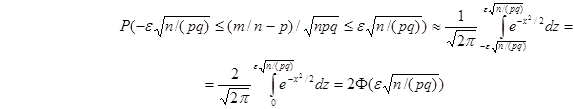Наконец, заменив неравенства, заключенные в скобках, равносильным им исходным неравенством, окончательно получим

.

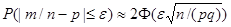Итак, вероятность осуществления неравенства 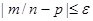приближённо равна значению удвоенной функции Лапласа 2Ф(х) при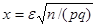

Пример 1. Вероятность того, что деталь не стандартна, р=0,1 Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности р=0,1 по абсолютной величине не более чей на 0,03

Решение. По условию, n = 400; р = 0,1; q=0,9; 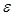=0,03. Тре­буется найти вероятность 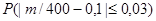. Пользуясь формулой 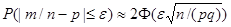, имеем

.

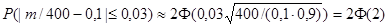По таблице приложения 2 находим Ф(2) = 0,4772. Следовательно, 2Ф(2)=0,9544.

Итак, искомая вероятность приближенно равна 0,9644.

Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности р=0,1 по абсолютной величине не превысит 0,03.

Пример 2. Вероятность того, что деталь не стандартна, р=0,1 Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не более чем иа 0,03.

Решение. По условию, р=0,1; q = 0,9: 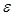= 0,03; 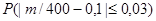= 0,9544. Требуется найти n.

Воспользуемся формулой

.

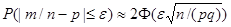В силу условия

.

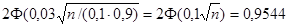Следовательно, .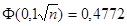

По таблице приложения 2 находим Ф (2) = 0,4772.

Для отыскания числа n получаем уравнение 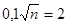. Отсюда искомое число деталей n = 400.

Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей, то в 96,44% этих проб относи­тельная частота появления нестандартных деталей будет отличаться от постоянной вероятности р=0,1 по абсолютной величине не более чем на 0,03, т. е. относительная частота заключена в границах от 0,07 (0,1-0,03=0,07) до 0,13 (0,1+0,03=0,13). Другими словами, число нестандартных деталей в 96,44% проб будет заключено между 28 (7% от 400) и 62 (13% от 400).

Если взять лишь одну пробу на 400 деталей, то с большой уверенностью можно ожидать, что в этой пробе будет нестандартных деталей не менее 28 и не более 63. Возможно, хотя и маловероятно, что нестандартных деталей окажется меньше 26 либо больше 52.

Задачи

1. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы.

Ответ а) Р₆(4) = 0,246; б) Р₆(6) = 0,26; в) Р₆(0) = 0,000064.

2. Найтн вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3.

Ответ .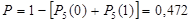

3. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 6 независимых испытаний, в каждом из которых вероятность появления события А равна 0,4.

Ответ .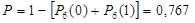

4. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, событие А появится хотя бы 2 раза.

Ответ .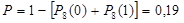

5. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз.

Ответa) 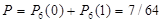; б) .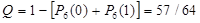

6. Вероятность попадания в цель при одном выстреле из орудия р=0,9. Вероятность поражения цели при k попаданиях ( 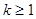) равна 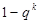. Найти вероятность того, что цель будет поражена, если сделано два выстрела.

Указание. Воспользоваться формулами Бернулли и полной вероятности.

Ответ 0,9639.

7. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.

Ответ Р₄₀₀(104) = 0,0006.

8. Вероятность поражения мишени стрелком при одном выстреле 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз.

Ответ а) Р₁₀₀(70,80) = 2Ф(1,15)=0.7498;

б) Р₁₀₀(0; 70)=-Ф(1,15) + 0,5 = 0,1251.

9. Вероятность появления события в каждом из 10 000 независимых испытаний р=0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001.

Ответ Р = 2Ф(0,23)=0,182.

10. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях.

Ответ 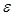= 0,00967.

11. Сколько раз надо бросить монету, чтобы с вероятностью 0,6 южно было ожидать, что отклонение относительной частоты появле­ний герба от вероятности р=0,5 окажется по абсолютной величине не более 0,01?

Ответ n=1764.