Распределение Пуассона
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений со бытия в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала ( 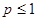 ). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно 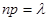 . Как будет следовать из дальнейшего (см. гл. VII, § 5), это означает, что среднее число появлений событии в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
. Как будет следовать из дальнейшего (см. гл. VII, § 5), это означает, что среднее число появлений событии в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
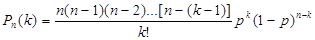 .
.
Так как 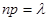 , то
, то 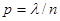 Следовательно,
Следовательно,
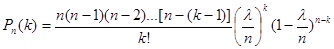 .
.
Приняв во внимание, что n имеет очень большое значение, вместо Рn(k) найдем 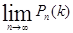 . При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение пр сохраняет постоянное значение, то при
. При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение пр сохраняет постоянное значение, то при 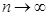 вероятность
вероятность 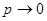 .
.
Итак,
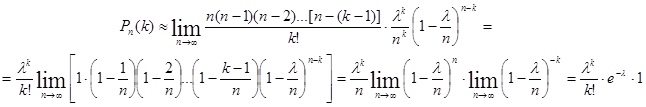 .
.
Таким образом (для простоты записи знак приближенства равенства опущен),
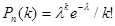
Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий.
Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Рn(k), зная k и 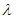 .
.
Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение. По условию, n = 5000, р=0,0002, k = 3. Найдем 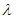 :
:
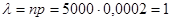 .
.
По формуле Пуассона искомая вероятность приближенно равна
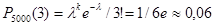 .
.
Дата добавления: 2016-03-27; просмотров: 960;
