Простейший поток событий

Рассмотрим события, которые наступают в случайные моменты времени.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примерами потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов и многие другие.

Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последействия ординарности.

Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. Например, вероятности появления k событий на промежутках времени (1; 7), (10; 16), (Т;T+ 6) одинаковой длительности t=6 ед. времени равны межлу собой.

Итак, если поток обладает свойством стационарности, то вероятность появления k событий за промежуток времени длительности t есть функция, зависящая только от k и t.

Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими cловами, условная вероятность появления k событий на любом промежутке времени, вычисленная при любых предположениях о том, что происходило до начала paссматриваемого промежутка (сколько событий появилось, в какой последовательности), равна безусловной вероятности. Таким образом, предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.

Итак, если поток обладает свойством отсутствие последействия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью появления только одного события.

Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.

Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.

Замечание. Часто на практике трудно установить, обладает ли поток перечисленными выше свойствами. Поэтому были найдены и другие условия, при соблюдении которых поток можно считан простейшим или близким к простейшему. В частности, установлено, что если поток представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный поток (при условии его ординарности) близок к простейшему.

Интенсивностью потока 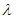называют среднее число событий, которые появляются в единицу времени.

Можно доказать, что если постоянная интенсивность известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона

.

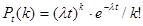Эта формула отражает все свойства простейшего потока.

Действительно, из формулы видно, что вероятность появления k событий за время t, при заданной интенсивности является функцией k и t, что характеризует свойство стационарности.

Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последействия.

Убедимся, что формула отражает свойство ординарности. Положив k=0 и k=1, найдем соответственно вероятности непоявления событий и появления одного события:

, .

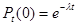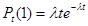Следовательно, вероятность появления более одного события

.

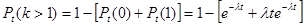Пользуясь разложением

,

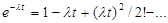после элементарных преобразований получим

.

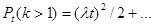Сравнивая P_t(0) и P_t(k > 1), заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.

Итак, формулу Пуассона можно считать математической моделью простейшего потока событий.

Пример. Среднее число вызовов, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за 5 минут поступит: а) 2 вызова; б) менее двух вызовов; в) не менее двух вызовов. Поток вызовов предполагается простейшим.

Решение. По условию, 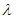=2, t=5, k=2. Воспользуемся формулой Пуассона

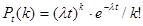
а) Искомая вероятность того, что за 5 минут наступит 2 вызова,

.

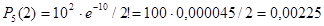Это событие практически не возможно

б) Событие «не наступило ни одного вызова» и «поступил один вызов» несовместны, поэтому по теореме сложения искомая вероятность того, что за 5 минут поступит менее двух вызовов, равна

.

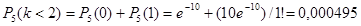Это событие практически не возможно.

в) События «поступило менее 2 вызовов» и «поступило не менее двух вызовов» противоположны, поэтому искомая вероятность того, что за 5 минут поступит не менее двух вызовов,

.

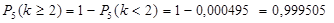Это событие практически достоверно.