Вероятность N аварий и оценка риска аварийности в зависимости от параметра lτ, согласно распределению Пуассона

N	0,1	0,2	0,3	0,5	1,0	2,0	3,0	4,0	5,0
	0,905	0,819	0,741	0,607	0,368	0,135	0,050	0,018	0,007
	0,091	0,164	0,222	0,303	0,368
	0,0045	0,016	0,033	0,076	0,184	0,271
	0,0002	0,0011	0,0033	0,013	0,061	0,180	0,224
		0,0001	0,0003	0,0016	0,015	0,090	0, 168	0,195
				0,0002	0,003	0,036	0,101	0,156	0,176
	0,095	0,181	0,259	0,393	0.632	0,865	0,950	0,982	0,993

Закон Пуассона является частным (предельным) случаем биномиального распределения при большом числе маловероят­ных событий. В связи с этим формулу Пуассона называют законом редких явлений. На рис. 10.2 показано распределение Пуассона для нескольких значений λτ, из которого видно, что при больших значениях λτ (λτ ³ 10) распределение приближа­ется к нормальному распределению при μ = σ² = λτ

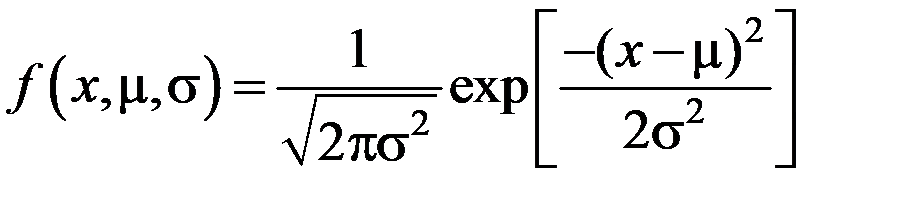. (10.8)

Закон Пуассона широко используют на практике: в теории надежности, при проверке качест­ва, при прогнозировании сейсмического риска и др. Закон Пу­ассона применим также к событиям (авариям), разбросанным на площадях. В этом случае параметр λ имеет смысл средней плотности, отнесенной не к временному интервалу, а к неко­торой площади.

1,0	Q
0,8
0,6
0,4
0,2	N=1
					5 λτ

Рис. 10.1. Вероятность аварий и оценка риска 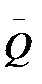аварийности
в зависимости от параметра λτ

0,6 Q 0,3 Q

λτ = 0,5 λτ = 1

0 2 4 N 0 3 6 N

0,2 Q λτ = 2 0,15 Q λτ = 4

0 3 6 N 0 5 10 N

0,12 Q λτ = 8 0,1 Q λτ =10

0 10 20 N 0 10 20 N

Рис. 10.2. Распределение Пуассона для шести значений λτ

Известен пример исключитель­но хорошего согласия с распределением Пуассона реальной статистики падений самолетов-снарядов в южной части Лон­дона в период Второй мировой войны. Такое согласие установ­лено при подсчете числа k падений, приходящихся на каждый из Ν = 576 одинаковых участков территории, каждый площадью S = 0,25 км². При общем числе снарядов Т = 537 число участков Nk, на которое приходилось по k падений (среднее число λS = Т/N –0,9323), дано в табл. 10.4 в сравнении со значениями вероятностей Р(k; 0,9323), подсчитанных по фор­муле Пуассона.

Таблица 10.4