Применение распределения Пуассона для оценки риска аварий

Оценка степени риска поражения людей и нанесения ущер­ба при авариях связана с задачей прогнозирования показате­лей надежности и остаточного ресурса функционирующей сис­темы. Наиболее важным вопросом является установление допустимых сроков дальнейшей эксплуатации индивидуального объекта при конкретном значении риска аварии. Ответствен­ность за соответствующие инженерные решения о мерах по снижению риска или о приостановке функционирования объ­екта лежит на комиссии, в состав которой должны входить специалисты-эксперты и представители административных ор­ганов.

Одним из основных показателей надежности объекта явля­ется вероятность P(t) безотказной работы на некотором вре­менном интервале (функция надежности). Функция Q(t) =1 – P(t),дополняющая P(t) до единицы и характеризующая вероятность отказа, является функцией риска аварии – поражения людей и нанесения материального ущерба.

Для оценки риска применяют модели теории на­дежности. Среди них модели высоконадежных систем, для которых аварийные ситуации явление редкое, а также модели стареющих систем, качество которых в процессе эксплуатации ухудшается вследствие ползучести, различных видов усталости, износа и других видов повреждений.

Прогнозирование аварийных ситуаций возможно на основе элементарной статистики и дискретного распределения Пуассона, часто применяемого к редким событиям и природным явлениям.

Функцией риска аварии из-за отказа нормального функционирования объекта называют вероятность отказа:

H(t) = 1 – P'(t), P'(t) = exp (–∫ λ (ξ) d ξ), (10.1)

λ(t) = – P'(t) / P(t),

где Р(t) – вероятность безотказной работы (функция надежно­сти); λ(t) – интенсивность отказов, равная вероятности того, что после безотказной работы до момента времени t авария произойдет в последующем малом отрезке времени.

Опыт показывает, что после небольшого начального периода эксплуатации (приработки) функция λ(t) длительный период достаточно стабильна, т. е. λ(t) = const. Влияние интенсивного старения за счет коррозионного износа, усталости и других факторов должно исключаться регламентированием допусти­мого срока службы.

Принимая для периода нормального (спокойного) функцио­нирования
λ(t) = const, из (10.1) получают экспоненциальное распределение

P(t) = exp(–λτ), (10.2)

причем θ = 1/λ – математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска те­перь можно записать в виде

H(t) = 1 – exp(– t/θ). (10.3)

При функции надежности в виде (10.2) частота отказов в системе однотипных объектов (поток случайных событий) со­ответствует дискретному распределению Пуассона

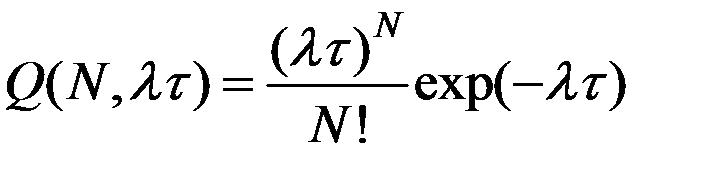, N = 0,1,2,… λτ > 0 . (10.4)

Согласно данной формуле, аварии на временном интервале τ (t, t + τ) произойдут N раз с вероятностью Q(N, λτ), а от­сутствие аварийных ситуаций (отсутствие отказов) – с вероятностью

Q(0,λτ) = exp(– λτ).(10.5)

Вероятность того, что аварии произойдут n разпри n < N (т. е. менее
N раз), определяется функцией распределения

Q₀(n<N)= 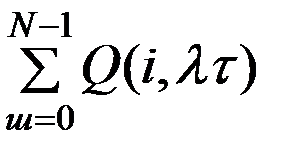=1 – φ(N,λτ) (10.6)

φ(N, λτ)= Q₀(n≥N)= .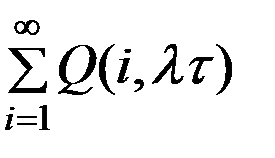

Вероятность возникновения хотя бы одной аварии пред­ставляет оценку риска аварий на объекте в период τ

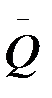= 1– Q(0, λτ) = 1 – exp(–λτ) . (10.7)

Для математического ожидания Ν, дисперсии D и стандар­та σ (среднеквадратического отклонения) имеет место равен­ство N = D = σ²= λτ, т. е. имеется возможность экспериментальной проверки правдоподобия гипотезы о применимости закона Пуассона к конкретному виду аварии по факту хотя бы приблизительного соблюдения равенства N = D.

Таким образом, прогнозирование аварийных ситуаций воз­можно на основе элементарной статистики. Такого рода дан­ные представляют интерес при принятии решений о мерах по снижению степени риска аварий на объектах.

Значения вероятности аварий Q(N, λτ) для числа N ≤ 5 и риска возможной аварии 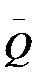приведены в табл. 10.3 и на рис. 10.1.

Таблица 10.3