Формула полной вероятности
Пусть событие А может наступить при условии появления одного из несовместных событий 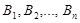 , которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности
, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности 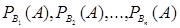 события А. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.
события А. Как найти вероятность события А? Ответ на этот вопрос дает следующая теорема.
Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий 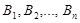 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
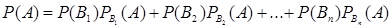 .
.
Эту формулу называют «формулой полной вероятности».
Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий 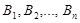 . Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий
. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий 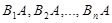 . Пользуясь для вычисления вероятности события А теоремой сложения, получим
. Пользуясь для вычисления вероятности события А теоремой сложения, получим
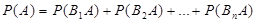 . (*)
. (*)
Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем
 .
.
Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности
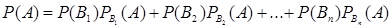 .
.
Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго - 0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.
Решение. Обозначим через А событие «извлеченная деталь стандартная».
Деталь может быть извлечена либо из первого набора (событие 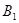 ) либо на второго (событие
) либо на второго (событие  ).
).
Вероятность того, что деталь вынута на первого набора, 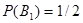
Вероятность того, что деталь вынута из второго набора, 
Условная вероятность того, что из первого набора будет извлечена стандартная деталь, 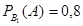 .
.
Условная вероятность того, что из второго набора будет извлечена стандартная деталь, 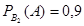 .
.
Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности равна
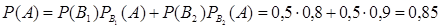 .
.
Пример 2. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная на первой коробки, будет стандартной.
Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа».
Из второй коробки могла быть извлечена либо стандартная лампа (событие 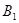 ), либо нестандартная (событие
), либо нестандартная (событие  ).
).
Вероятность того, что из второй коробки извлечена стандартная лампа, 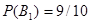 .
.
Вероятность того, что из второй коробки извлечена нестандартная лампа, 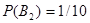 .
.
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна 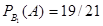 .
.
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна 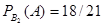 .
.
Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна
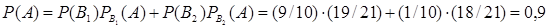 .
.
Дата добавления: 2016-03-27; просмотров: 1196;
