Независимые события. Теорема умножении для независимых событий
Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
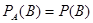 . (*)
. (*)
Подставив (*) в соотношение (***) предыдущего параграфа, получим
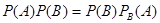 .
.
Отсюда
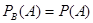 ,
,
т. е. условная вероятность события А в предположении, что наступило событие В, равна его безусловной вероятности. Другими словами, событие А не зависит от события В.
Итак, если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.
Для независимых событий теорема умножения 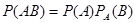 имеет вид
имеет вид
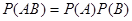 , (**)
, (**)
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Равенство (**) принимают в качестве определения независимых событий.
Два события называют независимыми, если вероятность совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.
На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
Пример 1. Найти вероятность совместного поражения цели двумя орудиями, если вероятность поражения цели первым орудием (событие А) равна 0,8, а вторым (событие В) - 0,7.
Решение. События А и В независимые, поэтому, по теореме умножения, искомая вероятность
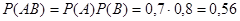 .
.
Замечание 1. Если события А и В независимы, то независимы также события А и 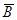 ,
, 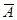 и В,
и В, 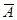 и
и 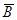 . Действительно,
. Действительно,
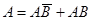 .
.
Следовательно,
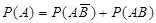 , или
, или 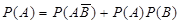 .
.
Отсюда
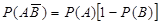 , или
, или 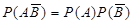 ,
,
т. е. события А и В независимы.
Независимость событий 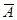 и В, А и
и В, А и 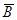 - следствие доказанного утверждения.
- следствие доказанного утверждения.
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности.
Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события 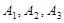 независимы в совокупности, то независимы события A1 и A2, A1 и А3, A2 и А3; A1 и А2 А3; А2 и A1 А3; А3 и A1 А2. Из сказанного следует, что если события независимы в совокупности, то условная вероятность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие события из числа остальных, равна его безусловной вероятности.
независимы в совокупности, то независимы события A1 и A2, A1 и А3, A2 и А3; A1 и А2 А3; А2 и A1 А3; А3 и A1 А2. Из сказанного следует, что если события независимы в совокупности, то условная вероятность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие события из числа остальных, равна его безусловной вероятности.
Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.
Поясним сказанное на примере. Пусть в урне имеется 4 шара, окрашенные: один – в красный цвет (А), один – в синий цвет (В), один – в черный цвет (С) и один – во все эти три цвета (ABC). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?
Так как из четырех шаров два имеют красный цвет, то Р(А) = 2/4 = 1/2. Рассуждая аналогично, найдем Р (В) = 1/2, Р (С) = 1/2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие В уже произошло. Изменится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события А? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-прежнему равна 1/2. Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна его безусловной вероятности. Следовательно, события А и В независимы. Аналогично придем к выводу, что события А и С, В и С независимы. Итак, события А, В и С попарно независимы.
Независимы ли эти события в совокупности? Оказывается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице. Другими словами, условная вероятность РВС(А)=1 события А не равна его безусловной вероятности Р (А) = 1/2. Итак, попарно независимые события А, В, С не являются независимыми в совокупности.
Приведем теперь следствие из теоремы умножения.
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей тих событий:
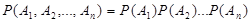 .
.
Доказательство. Рассмотрим три события: А, В и С. Совмещение событий А, В и С равносильно совмещению событий АВ и С, поэтому
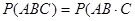 .
.
Так как события А, В и С независимы в совокупности, то независимы, в частности, события АВ и С, а также А и В. По теореме умножения для двух независимых событий имеем:
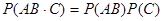 и
и 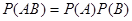 .
.
Итак, окончательно получим
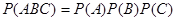 .
.
Для произвольного n доказательство проводится методом математической индукции.
Замечание. Если события 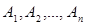 независимы в совокупности, то и противоположные им события
независимы в совокупности, то и противоположные им события 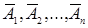 также независимы в совокупности.
также независимы в совокупности.
Пример 2. Найти вероятность совместного появления герба при одном бросании двух монет.
Решение. Вероятность появления герба первой монеты (событие А)
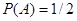 .
.
Вероятность появления герба второй монеты (событие В)
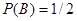 .
.
События А и В независимые, поэтому искомая вероятность по теореме умножения равна
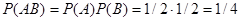 .
.
Пример 3. Имеется 3 ящика, содержащий по 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика вынута стандартная деталь (событие А),
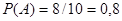 .
.
Вероятность того, что из второго ящика вынута стандартная деталь (событие В),
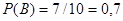 .
.
Вероятность того, что из третьего ящика вынута стандартная деталь (событие С),
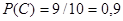 .
.
Так как события А, В и С независимые в совокупности, то искомая вероятность (по теореме умножения) равна
 -
-
Приведем пример совместного применения теорем сложения и умножения.
Пример 4. Вероятности появления каждого из трех независимых событий 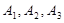 соответственно равны
соответственно равны 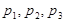 . Найти вероятность появления только одного из этих событий.
. Найти вероятность появления только одного из этих событий.
Решение. Заметим, что, например, появление только первого события А1 равносильно появлению события 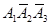 (появилось первое и не появились второе и третье события). Введем обозначения:
(появилось первое и не появились второе и третье события). Введем обозначения:
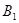 – появилось только событие А1, т. е.
– появилось только событие А1, т. е. 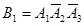 ;
;
 - появилось только событие А2, т. е.
- появилось только событие А2, т. е. 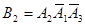 ;
;
 - появилось только событие А3, т. е.
- появилось только событие А3, т. е. 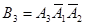 .
.
Таким образом, чтобы найти вероятность появления только одного из событий 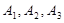 , будем искать вероятность
, будем искать вероятность 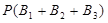 появления одного, безразлично какого из событий
появления одного, безразлично какого из событий 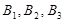 .
.
Так как события 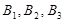 несовместны, то применима теорема сложения
несовместны, то применима теорема сложения
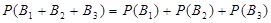 . (*)
. (*)
Остается найти вероятности каждого из событий 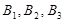 .
.
События 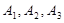 независимы, следовательно, независимы события
независимы, следовательно, независимы события 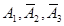 поэтому к ним применима теорема умножения
поэтому к ним применима теорема умножения
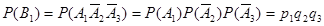
Аналогично,
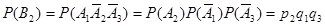
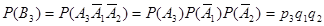
Подставив эти вероятности в (*), найдем искомую вероятность появления только одного из событий 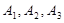 :
:
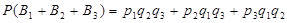 .
.
Дата добавления: 2016-03-27; просмотров: 1712;
