Принцип практической невозможности маловероятных событий

При решении многих практических задач приходится иметь дело с событиями, вероятность которых весьма мала, т. е. близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не пойдет? Такого заключения сделать нельзя, так как не исключено, хотя и мало вероятно, что событие А наступит.

Казалось бы, появление или непоявление маловероят­ного события в единичном испытании предсказать невозможно. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает. На основании этого факта принимают следующий «принцип практической невозможности маловероятных событий»: если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это собы­тие не наступит.

Естественно возникает вопрос: насколько малой должна быть вероятность события, чтобы можно было считать невозможным его появление в одном испытании? На этот вопрос нельзя ответить однозначно. Для задач, различных по существу, ответы разные. Например, если, вероятность того, что парашют при прыжке не раскроется, равна 0,01, то было бы недопустимым применять такие парашюты. Если же вероятность того, что поезд дальнего следования прибудет с опозданием, равна 0,01, то можно практически быть уверенным, что поезд прибудет вовремя.

Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключённые между 0,01 и 0,05. Уровень значимости, равный 0,01, называют однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным, и т. д.

Подчеркнем, что рассмотренный здесь принцип позво­ляет делать предсказания не только о событиях, имею­щих малую вероятность, но и о событиях, вероятность которых близка к единице. Действительно, если событие А имеет вероятность, близкую к нулю, то вероятность противоположного события 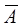близка к единице. С другой стороны, непоявление события А означает наступлении противоположного события 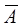. Таким образом, из прин­ципа невозможности маловероятных событий вытекает следующее важное для приложений следствие: если слу­чайное событие имеет вероятность, очень близкую к еди­нице, то практически можно считать, что в единичном испытании это событие наступит. Разумеется, и здесь ответ на вопрос о том, какую вероятность считать близ­кой к единице, зависит от существа задачи.

Задачи

1. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?

Ответ р=0,02.

2. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероят­ность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

Ответ р = 0,4.

3. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.

Ответ р = 44/45.

4. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной детали.

Ответ р = 2/3.

Указание. Если А — нет ни одной нестандартной детали, В— есть одна нестандартная деталь, то

.

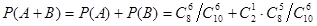5.События А, В, С и D образуют полную группу. Вероятности событий таковы: Р(А)=0,1; Р(В)=0,4; P(С)=0,3. Чему равна вероятность события D?

Ответ P(D) = 0,2.

6. По статистическим данным ремонтной мастерской, в среднем остановок токарного станка приходится: 10—для смены резца; 3 – из-за неисправности привода; 2—из-за несвоевременной подачи заготовок. Остальные остановки происходят по другим причинам. Найти вероятность остановки станка по другим причинам.

Ответ р = 0,25.