Геометрические вероятности
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.). Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством
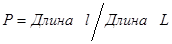 .
.
Пример 1. На отрезок ОА длины l- числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой сен.
Решение. Разобьем отрезок ОА точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины L/3. Искомая вероятность
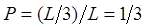 .
.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством
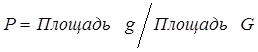 .
.
Пример 2. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.
Решение. Площадь кольца (фигуры g)
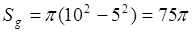 .
.
Площадь большого круга (фигуры G)
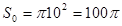 .
.
Искомая вероятность
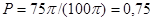 .
.
Пример 3. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше 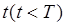 . Найти вероятность того, что сигнализатор сработает за время Т, если каждое из устройств пошлет по одному сигналу.
. Найти вероятность того, что сигнализатор сработает за время Т, если каждое из устройств пошлет по одному сигналу.
|
Решение. Обозначим моменты поступления сигналов первого и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства: 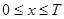 ,
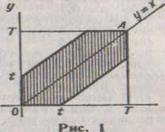
, 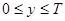 . Введём в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТАТ (рис. 1). Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют возможные значения моментов поступления сигналов.
. Введём в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТАТ (рис. 1). Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют возможные значения моментов поступления сигналов.
Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т. е. если 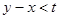 при
при 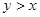 и
и 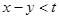 при
при 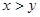 , или что то же,
, или что то же,
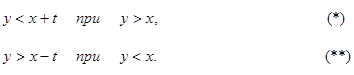
Неравенство (*) выполняется для тех точек фигуры G, которые выше прямой у=х и ниже прямой 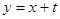 неравенство (**) имеет место для точек, расположенных ниже прямой у=х и выше прямой у = x-t.
неравенство (**) имеет место для точек, расположенных ниже прямой у=х и выше прямой у = x-t.
Как видно нз рис. 1, все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному прямоугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими моментами времени х и у.
Искомая вероятность
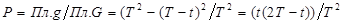 .
.
Замечание 1. Приведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g—часть области G, равна
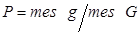 .
.
Замечание 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения не имеют места. Например, вероятность попадания брошенной точки в одну определённую точку области G равна нулю, однако это событие может произойти, и, следовательно, не является невозможным.
Задачи
1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
Ответ р = 0,1.
2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.
Ответ. р = 0,5.
3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
Ответ р=0,81.
4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».
Ответ р=1/120.
5. На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных «в одну линию» карточках можно будет прочесть слово «трос».
Ответ 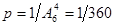
6. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три.
Ответ а) 0,384; б) 0,096; в) 0,008.
7. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найтн вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем; б) не есть дубль.
Ответ а) 2/9; б) 4/9.
8. В замке на общей оси пять дисков. Каждый-диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найтн вероятность того, что при произвольной установке дисков замок можно будет открыть.
Ответ 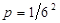 .
.
9. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
Ответ 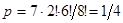 .
.
10. Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги—по одному рублю и две книги — по 3 рубля. Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.
Ответ 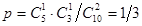 .
.
11. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?
Ответ 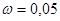 .
.
12. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего произведено 120 выстрелов.
Ответ 102 попадания.
15. На отрезок ОА длины L числовой оси Ох наудачу поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, меньшую, чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Ответ р = 2/3.
14. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в крут квадрата. Предполагается, что вероятность попадания точки в квадрат пропорциональна площади квадрата и не зависит от его расположения относительно круга.
Ответ 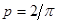
16. Задача о встрече. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найтн вероятность того, что встреча состоится, если каждый студент наудачу выберет момент своего прихода (в промежутке от 12 до 13 часов).
Указание. Ввести в рассмотрение прямоугольную систему координат хОу и принять для простоты, что встреча должна состояться между 0 и I часами.
Ответ Возможные значения координат: 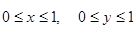 ; благоприятствующие встрече значения координат:
; благоприятствующие встрече значения координат: 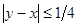 ;
; 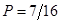 .
.
Дата добавления: 2016-03-27; просмотров: 6605;
