Теорема умножения вероятностей
Рассмотрим два события: А и В; пусть вероятности Р (А) и  известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Доказательство. По определению условной вероятности,
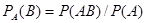 .
.
Отсюда
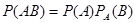 . (*)
. (*)
Замечание. Применив формулу (*) к событию ВА, получим
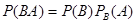 ,
,
или, поскольку событие ВА не отличается от события АВ,
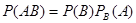 . (**)
. (**)
Сравнивая формулы (*) и (**), заключаем о справедливости равенства
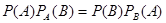 . (***)
. (***)
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появилось
 ,
,
где 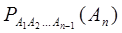 - вероятность события
- вероятность события 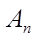 , вычисленная в предположении, что события
, вычисленная в предположении, что события 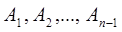 наступили. В частности, для трёх событий
наступили. В частности, для трёх событий
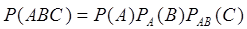 .
.
Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т. д.
Пример 1. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй- эллиптический.
Решение. Вероятность того, что первый валик окажется конусным (событие А),
Р(А) =3/10.
Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность
 .
.
По теореме умножения, искомая вероятность
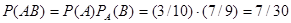 .
.
Заметим, что, сохранив обозначения, легко найдем: 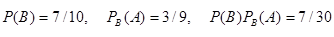 ,
,
что наглядно иллюстрирует справедливость равенства (***).
Пример 2. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В) и при третьем – синий (событие С).
Решение. Вероятность появления белого шара в первом испытании
Р(А) = 5/12.
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность
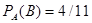 .
.
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором – черный, т. е. условная вероятность
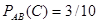 .
.
Искомая вероятность
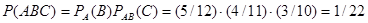 .
.
Дата добавления: 2016-03-27; просмотров: 793;
