Геометрический способ определения вероятностей
Данный способ применяют тогда, когда опыт относится к схеме случаев, но число благоприятных случаев и число равновозможных и несовместных случаев подсчитать невозможно, но можно поставить этим числам в однозначное соответствие определенные длины, площади, объемы и другие физические величины.
Пример 4: Имеется некоторый монтажный провод длиной L. Разрыв может произойти в любой точке с одинаковой вероятностью. Определить вероятность того, что разрыв произойдет на участке длиной l, если считать, что разрыв одновременно в нескольких точках невозможен.
Решение.
Поставив в соответствие числам m и n длины l и L, вероятность разрыва провода на участке l можно определить по формуле
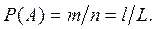
Рассмотренный пример иллюстрирует геометрическое определение вероятности: вероятность случайного события есть отношение длины участка благоприятного появлению события к длине всего провода.Геометрическое определение вероятности является обобщением классического определения на случай, когда число равновозможных исходов бесконечно.
Теоремы сложения и умножения вероятностей
Алгебра событий
Для успешного решения некоторых типовых задач необходимо познакомиться с очень важными понятиями: суммы и произведения событий.
Суммой событий A и B называют событие C=A+B, которое состоит в появлении хотя бы одного из этих событий.
Пример 1:Событие A – поражение цели при первом выстреле, событие B - поражение цели при втором выстреле.
Тогда суммой событий A+B будет поражение цели вообще (либо при первом выстреле, либо при втором, либо при первом и втором выстрелах).
Если события A и B совместны (пример 1), то сумма событий C=A+B сводится к появлению или события A, или события B, или и A, и B.
Если события A и B несовместны, то появление их вместе отпадает, а поэтому их сумма сводится к появлению или события A, или события B.
Например, при бросании монеты события: появление герба, появление цифры несовместны, поэтому сумма их сводится к появлению только одного из них.
Произведением A и B называют событие C=AB, которое состоит в совместном появлении событий A и B.
Пример 2:Если событие A – попадание в «десятку» при первом выстреле, событие B – попадание в «десятку» при втором выстреле и событие C – попадание в «десятку» при третьем выстреле, то произведение D=ABC – попадание в «десятку» при всех выстрелах.
При определении вероятностей часто приходится представлять сложные события в виде комбинаций элементарных событий, применяя и операцию сложения, и операцию умножения.
В условиях примера 2, события 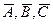 - непопадание в «десятку» при первом, втором и третьем выстрелах соответственно.
- непопадание в «десятку» при первом, втором и третьем выстрелах соответственно.
Составим сложное событие G, состоящее в том, что в результате трех выстрелов «десятка» будет поражена ровно один раз. Это событие может быть представлено в виде
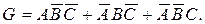
Дата добавления: 2016-04-19; просмотров: 1771;
