Теорема сложения вероятностей для совместных событий
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления. Т.е., если события A и B совместны, то
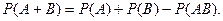
Доказательство.
Пусть испытание имеет n элементарных равновозможных исходов, из которых событию A благоприятны m исходов, событию B благоприятны k исходов, событию AB благоприятны l исходов, тогда
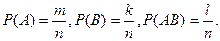
Число исходов, благоприятных сумме A+B событий A и B будет равно` 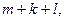 поэтому
поэтому
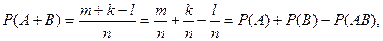
что и требовалось доказать.
В случае трех совместных событий вероятность их суммы вычисляется по формуле
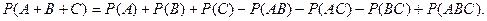
В случае же n совместных событий вероятность их суммы может вычисляться по формуле
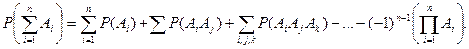
Пример 3:Три стрелка стреляют по одной цели. Найти вероятность поражения цели при одном залпе, если вероятности поражения цели соответственно равны: 0,8; 0,8; и 0,9.
Решение.
Рассмотрим события:
A – поражение цели;
B – поражение цели I - м стрелком (I =1,2,3).
Так как требуется определить вероятность поражения цели вообще, то событие A есть сумма событий 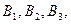 являющихся совместными и независимыми. Поэтому
являющихся совместными и независимыми. Поэтому
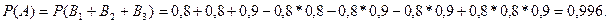
Теорема сложения вероятностей для несовместных событий.Вероятность суммы нескольких несовместных событий равна сумме вероятностей этих событий, т.е. 
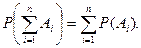
Эта теорема является частным случаем теоремы сложения вероятностей для несовместных событий.
Следствия из теоремы.
Следствие 1. Если события 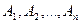 несовместны и образуют полную группу, то
несовместны и образуют полную группу, то
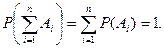
Следствие 2. Два несовместных события, образующих полную группу, называют противоположными событиями. Сумма вероятностей противоположных событий равна единице, т.е.
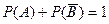 .
.
Дата добавления: 2016-04-19; просмотров: 1498;
