Векторный закон сложения скоростей
Всякое движение, а также покой (как частный случай движения) относительны. Абсолютного движения не существует. Оно всегда происходит только по отношению к телу, которое мы условно считаем неподвижным. Данные о положении и скорости тела будут иметь смысл только тогда, когда мы укажем систему отсчета.
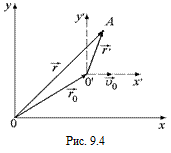 Выясним, как связаны между собой движения точки в различных системах отсчета х0у и х¢0у¢ (для краткости: K-система и K¢-система, на рис. 9.4). При этом K¢-система движется поступательно по отношению к неподвижной K-системе.
Выясним, как связаны между собой движения точки в различных системах отсчета х0у и х¢0у¢ (для краткости: K-система и K¢-система, на рис. 9.4). При этом K¢-система движется поступательно по отношению к неподвижной K-системе.
Пусть в K-системе начало координат K¢-системы характеризуется радиусом-вектором 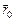 , а ее скорость
, а ее скорость 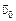 . Если положение точки А в K-системе, определяемой радиусом-вектором
. Если положение точки А в K-системе, определяемой радиусом-вектором 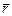 , а в K¢-системе – радиусом-вектором
, а в K¢-системе – радиусом-вектором 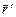 , то, как видно из рис. 9.4,
, то, как видно из рис. 9.4, 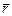 =
= 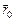 +
+ 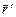 . Далее, пусть за промежуток времени Dt точка А совершит в K-системе элементарное перемещение
. Далее, пусть за промежуток времени Dt точка А совершит в K-системе элементарное перемещение 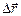 . Это перемещение складывается из перемещения
. Это перемещение складывается из перемещения 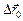 вместе с K¢-системой и перемещением
вместе с K¢-системой и перемещением 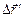 относительно K¢-системы, т.е.
относительно K¢-системы, т.е. 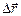 =
= 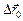 +
+ 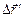 .
.
Разделим данное выражение на Dt и получим формулу преобразования скорости:
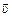 =
= 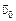 +
+ 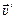 . (9.5)
. (9.5)
Таким образом, скорость точки в неподвижной системе отсчета равна сумме скоростей подвижной системы отсчета и скорости точки относительно подвижной системы, если последняя движется поступательно.
Заметим, что скорость тела в неподвижной системе отсчета (с.о.) 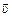 условились называть абсолютной, скорость тела в движущейся с.о.
условились называть абсолютной, скорость тела в движущейся с.о. 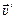 – относительной, а скорость подвижной с.о. относительно неподвижной с.о.
– относительной, а скорость подвижной с.о. относительно неподвижной с.о. 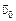 – переносной.
– переносной.
Простой пример: пассажир идет вдоль вагона поезда со скоростью 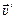 , сам поезд движется поступательно относительно земли со скоростью
, сам поезд движется поступательно относительно земли со скоростью 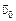 . Тогда очевидно, что скорость пассажира относительно земли определится формулой (9.5).
. Тогда очевидно, что скорость пассажира относительно земли определится формулой (9.5).
Теперь рассмотрим случай, когда в некоторой с.о. два тела движутся независимо друг от друга. Как определяется их движение относительно друг друга?
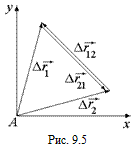 Пусть из некоторой точки А на берегу отплывают две лодки, одна из которых удаляется от А на расстояние
Пусть из некоторой точки А на берегу отплывают две лодки, одна из которых удаляется от А на расстояние 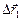 , а другая – на расстояние
, а другая – на расстояние 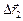 (рис. 9.5).
(рис. 9.5).
Очевидно, что относительное их перемещение определяется взаимным расстоянием 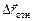 , значит, относительное перемещение равно разности
, значит, относительное перемещение равно разности 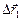 и
и 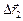 . При этом перемещение первой лодки относительно второй
. При этом перемещение первой лодки относительно второй 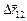 =
= 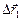 –
– 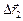 , а перемещение второй лодки относительно первой равно
, а перемещение второй лодки относительно первой равно 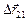 =
= 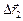 –
– 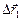 . Отсюда
. Отсюда 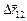 = –
= – 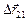 . Деля перемещения на время, за которое они произошли, получаем
. Деля перемещения на время, за которое они произошли, получаем
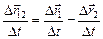 ,
, 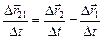
или
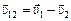 ,
, 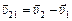 . (9.6)
. (9.6)
Таким образом, относительные перемещение и скорость двух тел определяются векторной разностью их перемещений и скоростей, заданных по отношению к одной и той же с.о.
Рассмотрим задачи на применение векторного закона сложения скоростей.
Переправа
Задача 9.1. Человеку на лодке необходимо переправиться через реку так, чтобы попасть из пункта А в пункт В (рис. 9.6,а). Скорость течения реки и, АС = L, СВ = а.
1. Какую минимальную скорость относительно воды может при этом иметь лодка? Как должна быть направлена эта скорость?
2. Какой будет скорость относительно берега?
3. За какое время лодка попадет из А в В?
| АС = L СВ = а и | а) 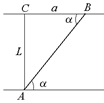 б) б) 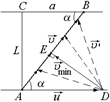 Рис. 9.6
Рис. 9.6
|
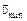 = ? = ?
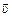 = ?
tп = ? = ?
tп = ?
| |
Решение. Скорость лодки относительно берега 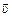 должна совпадать с линией АВ (рис. 9.6,б). При этом при любом из показанных на рисунке направлений скорости лодки относительно воды
должна совпадать с линией АВ (рис. 9.6,б). При этом при любом из показанных на рисунке направлений скорости лодки относительно воды 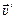 это условие будет выполнено. Но минимальным значение
это условие будет выполнено. Но минимальным значение 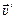 будет только в том случае, если
будет только в том случае, если 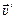 ^ АВ. Тогда из треугольника ADE легко найти
^ АВ. Тогда из треугольника ADE легко найти 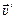 :
:
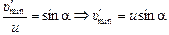 .
.
Из треугольника AВС найдем, что
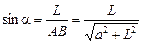 ,
, 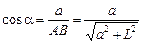 .
.
Тогда
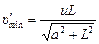 .
.
Абсолютную скорость 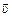 найдем из треугольника ADE:
найдем из треугольника ADE:
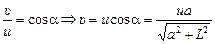 .
.
Время переправы
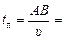
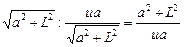 .
.
Ответ: 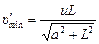 ;
; 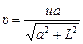 ;
; 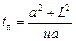 .
.
СТОП! Решите самостоятельно: С1, С2.
Дождь
Задача 9.2. Заднее стекло автомобиля составляет с горизонтом угол a = 60°. Идет вертикальный дождь, скорость капель которого равна υ1 = 10 м/с. При какой скорости автомобиля капли не будут попадать на заднее стекло?
| a = 60° υ1 = 10 м/с | а) 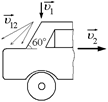 б) б) 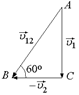 Рис. 9.7 Рис. 9.7
|
| υ2 = ? | |
Решение. Капли не будут попадать на заднее стекло, если их скорость 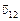 относительно автомобиля направлена так, как показано на рис. 9.7,а.
относительно автомобиля направлена так, как показано на рис. 9.7,а.
Согласно формуле (9.6) скорость капель относительно автомобиля 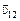 =
= 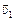 –
– 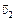 (рис. 9.7,б). Тогда из треугольника скоростей АВС легко найти минимальную скорость автомобиля, при которой капли не будут попадать на заднее стекло:
(рис. 9.7,б). Тогда из треугольника скоростей АВС легко найти минимальную скорость автомобиля, при которой капли не будут попадать на заднее стекло:
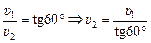 =
= 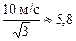 м/с.
м/с.
Ясно, что при υ2 > 5,8 м/с капли также не будут попадать на заднее стекло.
Ответ: υ2 ³ 5,8 м/с.
СТОП! Решите самостоятельно: В7–В8, С3.
Дата добавления: 2016-04-11; просмотров: 1850;
