Равномерное прямолинейное движение

Движение по прямой в заданном направлении называется прямолинейным движением.

Как мы уже знаем, движение называется равномерным, если материальная точка за рав­ные, произвольно выбранные промежутки времени, перемещается на рав­ные расстояния в заданном направлении или проходит равные пути. Движение называется неравномерным, если перемещения (или пути), пройденные точкой за произвольные равные промежутки времени, неодинаковые.

Количественной харак­теристикой равномерного прямолинейного движения является скорость. Скоростью 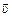называется физическая величина, равная отношению вектора перемеще­ния 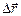к длительности промежутка времени Dt, за которое это перемещение произошло: 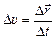. Направление вектора скорости совпадает с направлением вектора перемещения.

А теперь получим уравнение равномерного прямолинейного движе­ния точки в системе координат, оси которой не совпадают с направлением траектории.

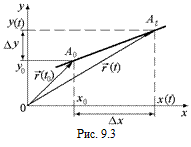Пусть материальная точка занимает последовательно положение А₀ и A_t, соответствующее моментам времени t₀ и t. На рис. 9.3 изображены радиусы-векторы и их проекции на оси 0х и 0у, характеризующие положения А₀ и A_t. Разность 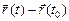является перемещением точки за промежуток времени (t–t₀). В этом случае скоростью точки является вектор

. (9.1)

Поскольку в равномерном движении скорость не зависит от времени, то 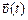= 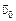, где 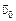– постоянный вектор скорости. Положение точки в любой момент времени, т.е. радиус-вектор 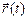можно найти из (9.1):

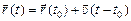. (9.2)

Это векторное соотношение равносильно определению двух скалярный функций

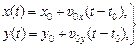(9.3)

где х₀, у₀ – координаты радиуса-вектора , υ_0хи υ_0у – проекции вектора скорости 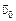на оси 0х и 0у.

Полагая для удобства t₀ = 0, получим компактную запись для проекций вектора перемещения, т.е. уравнение движения точки вдоль осей 0х и 0у:

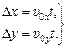(9.4)

Обратим внимание на то, что в нашем рассмотрении прямолинейное равномерное движение выглядит «сложным» движением, т.е. суммой двух движений. Это, конечно, связано с использованием «неудобной» системы координат. Если бы мы совместили ось 0х или ось 0у с траекторией, то для описания движения точки достаточно было бы одной координаты.