Задачи средней трудности. В1.Автомобили А и В движутся по взаимно перпендикулярным дорогам: первый – на север со скоростью 60 км/ч

В1.Автомобили А и В движутся по взаимно перпендикулярным дорогам: первый – на север со скоростью 60 км/ч, а второй – на восток со скоростью 80 км/ч. Какова скорость первого автомобиля относительно второго?

В2.Две прямые дороги пересекаются под углом a. От перекрестка по этим дорогам удаляются две машины: одна со скоростью υ₁, другая – со скоростью υ₂. Определить скорость, с которой одна машина удаляется от другой, учитывая, что перекресток они проехали одновременно.

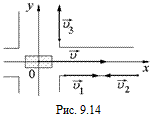
В3. В системе отсчета, связанной с землей, трамвай движется со скоростью υ = 2,4 м/с (рис. 9.14), а три пешехода – с одинаковыми по модулю скоростями υ₁ = υ₂ = υ₃ = 1,0 м/с. Найти: а) модули скоростей пешеходов в системе отсчета, связанной с трамваем; б) проекции векторов скоростей пешеходов на оси координат в этой системе отсчета.

В4. Бесконечный конус с углом раствора 90° движется с постоянной скоростью справа налево к центру покоящегося шара. Направление скорости совпадает с осью конуса. Шар разрывается на множество осколков, которые летят во все стороны равномерно с той же по модулю скоростью υ. Какая часть осколков попадает на конус? Влиянием силы тяжести пренебречь.

В5. Параллельный пучок одинаковых ядер движется со скоростью υ. Ядра в пучке начинают самопроизвольно делиться на две части одинаковой массы. Максимальная скорость осколков, движущихся в направлении пучка, равна и (в неподвижной системе отсчета). Найти скорость осколков, движущихся в направлении, перпендикулярном пучку.

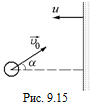В6. Гладкая вертикальная плита дви­жется горизонтально со скоростью и. Летящий в горизонтальной плоскости со скоростью υ₀ шарик соударяется с плитой. Направление полета шарика со­ставляет угол a с перпендикуляром к плите (рис. 9.15). Найти скорость υ шари­ка после соударения с плитой. Плита, обладая очень большой массой, не из­меняет своей скорости в результате со­ударения с шариком. Считать соударение абсолютно уп­ругим. Силой тяжести пренебречь.

В7.Однажды, стоя под дождем, я задумался: чему равна ско­рость капель? Прежде всего, я взял отвес и убедился, что капли падают строго вертикально. Затем я сел в карету и обнаружил, что во время езды следы капель на стекле кареты наклонены под углом a = 60° к горизонту. Тогда я спросил у лошади, с какой скоростью едет карета, и узнал, что ее скорость и = 30 км/ч. Тут же я рассчитал скорость υ капель относительно земли. Чему она была равна?

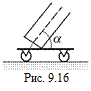В8. На тележке установлена труба, которая может поворачиваться в верти­кальной плоскости (рис. 9.16). Тележка равномерно движется по горизонталь­ному пути со скоростью υ₁ = 2,0 м/с. Под каким углом a к горизонту сле­дует установить трубу, чтобы капли дождя, падающие отвесно со скоростью υ­₂ = 6,0 м/с, двигались относительно трубы параллельно ее стенкам, не заде­вая их? Скорость капель вследствие сопротивления воздуха можно считать постоянной.

В9. Определить построением направ­ление флага на яхте (рис. 9.17). Скорость яхты 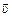, скорость ветра .

В10. Корабль идет на запад со скоростью υ_к = = 6,5 м/с. Ветер дует с юго-запада со скоростью υ_в = = 3,5 м/с. Какую скорость ветра υ_пр зарегистрируют приборы, расположенные на корабле? Каково будет показываемое этими приборами направление ветра относительно курса корабля?

В11. Корабль выходит из пункта А и идет со скоростью 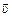, составляющей угол a с линией АВ (рис. 9.18). Под каким углом b к линии АВ следовало бы выпустить из пункта В торпеду, чтобы она поразила корабль? Торпеду нужно выпустить в тот момент, когда корабль будет находиться в пункте А. Скорость торпеды равна .

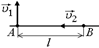
Рис. 9.18 Рис. 9.19 Рис. 9.20

В12. Две точки движутся со скоростям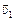и и 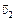так, как показано на рис. 9.19. Найти построением скорость первой точки относительно второй: . Оп­ределите модуль этой скорости, если a = b = 60°, . Определите пост­роением наименьшее расстояние между точками.

В13. Два автомобиля двигались с постоянными скоростям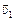и и 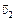по дорогам, пересекающим­ся под прямым углом (рис. 9.20). Когда первый из них достиг перекрёстка, второму оставалось проехать до этого места расстояние l. Спустя какое время t расстояние между автомобилями будет наименьшим? Чему равно это расстояние s­_min?

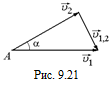В14.Два корабля движутся под углом a друг к другу со скоростям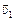и и 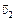(рис. 9.21). Найти относительную скорость кораблей и расстояние r₁₂ между ними в момент t. В начальный момент корабли находились в точке А.

В15.Корабль, проходящий точку А, движется с постоянной ско­ростью υ₀. Под каким углом b к прямой АВ надо начать двигаться катеру из точки В с постоянной скоростью υ₁, чтобы встретиться с кораблем? Линия АВ составляет угол y с перпендикуляром к курсу корабля (рис. 9.22).

В16.В условиях предыдущей задачи определить время t, по истечении которого катер встретится с кораблем, если первоначальное расстояние между ними равнялось АВ = l (см. рис. 9.22).

В17. На улице идет дождь. В каком случае ведро, стоящее в кузове грузового автомобиля, наполнится быстрее водой: когда автомобиль движется или когда он стоит?

В18. Ведро выставлено под дождь. Изменится ли скорость наполнения ведра водой, если подует ветер?

В19. Идет отвесный дождь. Скорость капель и. По асфальту со ско­ростью υ катится мяч. Другой такой же мяч лежит неподвижно. На какой мяч попадает больше капель? Во сколько раз?

Задачи трудные

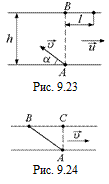С1. Лодочник, переправляясь через реку ширины h из пункта А в пункт В, все время направляет лодку под углом a к берегу (рис. 9.23). Найти скорость лодки υ относительно воды, если скорость течения реки равна и, а лодку снесло ниже пункта В на расстояние l.

С2.Из пункта А, расположенного на берегу реки, необходимо попасть в пункт В, двигаясь по прямой АВ. (рис. 9.24). Ширина реки AC = 1 км, расстояние ВС = 2 км, максимальная скорость лодки относительно воды и = 5 км/ч, а скорость течения реки υ = 2 км/ч. Можно ли проплыть расстояние АВ за 30 мин?

С3. При горизонтальном ветре, имеющем скорость υ_в1 = 10 м/с, капли дождя падают под углом a₁ = 30° к вертикали. При какой горизонтальной скорости ветра υ_в2 капли будут падать под углом a₂ = 60° к вертикали? Считать, что в безветренную погоду все капли падают с постоянной и одинаковой скоростью.

С4.Буер движется прямолинейно по гладкой ледяной поверхности со скоростью υ. Перпендикулярно к линии движения буера дует ветер со скоростью и = 2υ. Под каким углом b по отношению к плоскости паруса установится поме­щенный на мачте буера флюгер? Парус стоит под углом 45° к линии ветра.

С5.Корабль идет на запад со скоростью υ. Известно, что ветер дует с юго-запада. Скорость ветра, измеренная на палубе корабля, равна и₀. Найти скорость ветра и относи­тельно земли.

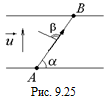С6. По реке из точки А в точку В, находящуюся на противоположном берегу, вдоль прямой АВ, образующей с линией берега угол a, плывет катер (рис. 9.25). Под прямым углом к берегу дует ветер со скоростью и. Флаг на мачте катера об­разует угол b с направле­нием движения катера. Оп­ределить скорость катера относительно берега. Мож­но ли по данным, приведен­ным в условии задачи, определить скорость течения реки?

С7. Два теплохода движутся с одинаковыми скоростями по прямолинейным траекториям в направлении точки О, причем их траектории пересекаются в этой точке под углом a = 60°. Первоначально теплоходы находились от этой точки на расстояниях l₁ = 20 км и l₂ = 30 км соответственно. Каким было минимальное расстояние х между теплоходами во время их движения?

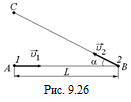С8. Тело 1 начинает двигать­ся из точки А по направлению к точке В со скоростью υ₁; одно­временно тело 2 начинает дви­гаться из точки В по направле­нию к точке С со скоростью υ₂ (рис. 9.26). Расстояние AB = L. Острый угол АВС = a. В какой момент времени t расстоя­ние l между телами 1 и 2 будет минимальным? Каково это расстояние?

С9. По пересекающимся под углом a дорогам движутся две автомашины с постоянными скоростями υ₁ и υ₂. Опре­делить величину и направление скорости одного автомо­биля относительно другого. Через какое время после встречи на перекрестке расстояние между машинами будет равно s?

С10. Автомашины (см. задачу С9) не встретились на пе­рекрестке, причем вторая машина проехала перекресток на промежуток времени τ позже первой. Каково было наи­меньшее расстояние между автомашинами?

С11. Круглое ядро радиуса R, движущееся со скоростью υ, пролетает сквозь рой мух, движущихся со скоростью и перпен­дикулярно направлению полета ядра. Толщина роя равна d (d >> R), в единице его объема в среднем находится п мух. Сколько мух убьет ядро? Влиянием силы тяжести пренебречь.