Относительная скорость движения
Задача 9.3.Два корабля движутся со скоростями 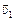 и
и 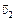 , как показано на рис. 9.8. Угол a и расстояние l заданы. Какова скорость второго корабля относительно первого? Каково наименьшее расстояние между кораблями? Через какое время корабли будут на этом расстоянии?
, как показано на рис. 9.8. Угол a и расстояние l заданы. Какова скорость второго корабля относительно первого? Каково наименьшее расстояние между кораблями? Через какое время корабли будут на этом расстоянии?
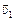 , , 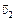 , a, l , a, l
|  Рис. 9.8
Рис. 9.8
|
 = ? smin = ?
t = ? = ? smin = ?
t = ?
| |
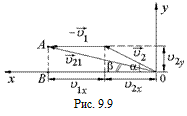 Решение. 1. Скорость второго корабля относительно первого равна
Решение. 1. Скорость второго корабля относительно первого равна  =
=  –
–  (рис. 9.9). Найдем проекции вектора
(рис. 9.9). Найдем проекции вектора  на оси х и у:
на оси х и у:
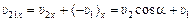 ;
;
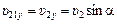 ;
;
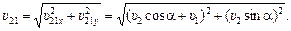
Угол b, который вектор  составляет с осью х, легко найти из DАОВ:
составляет с осью х, легко найти из DАОВ:
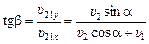 ,
,  .
.
2. Второй корабль будет двигаться относительно первого по прямой, направленной вдоль вектора  . Наименьшее расстояние
. Наименьшее расстояние 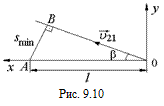 smin можно найти из DАОВ (рис. 9.10):
smin можно найти из DАОВ (рис. 9.10):
smin = lsinb.
3. Время, через которое корабли будут на минимальном расстоянии
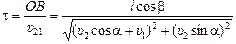 .
.
Ответ: 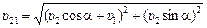 ;
;
 ;
; 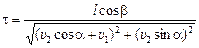 .
.
СТОП! Решите самостоятельно: В1, В2, В13, С7.
Флаг на корабле
Задача 9.4. Корабль движется на восток со скоростью υ1 = 10 м/с. При этом дует северо-западный ветер со скоростью υ2 = 5,0 м/с. Какова скорость ветра (по модулю) относительно корабля? Какой угол составляет флаг на мачте корабля с направлением движения корабля?
| υ1 = 10 м/с υ2 = 5,0 м/с | Решение. Плоскость флага всегда параллельна скорости ветра относительно корабля. Перейдем в с.о. «корабль». В этой с.о. скорость ветра будет равна 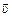 = =  – –  (рис. 9.11). Проекции скорости (рис. 9.11). Проекции скорости  на оси х и у равны: на оси х и у равны:
| |
| υ = ? a = ? | ||
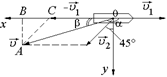 Рис. 9.11
Рис. 9.11
|  ; ; 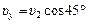 ; ;
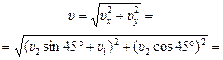
 м/с. м/с.
| |
Угол b найдем из DАВО:
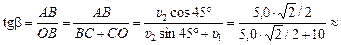 0,26.
0,26.
Откуда b = arctg 0,26 » 15°, а искомый угол a = 180° – b » 165°.
Ответ: υ » 14 м/с; a » 165°.
СТОП! Решите самостоятельно: В9, В10, С4.
Поток частиц
Пусть некоторые частицы (нейтроны, мухи, капли дождя и пр.) движутся с одинаковой скоростью в одном направлении и пусть концентрация частиц (т.е. их число в единице объема) равна п ([n] = 1/cм3). Определим число частиц, которое пересечет за время Dt площадку площадью S, такую, что нормаль 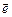 (вектор единичной длины, перпендикулярный к площадке) составляет угол a с вектором скорости частиц.
(вектор единичной длины, перпендикулярный к площадке) составляет угол a с вектором скорости частиц.
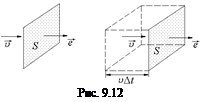 1. Пусть a = 0, т.е.
1. Пусть a = 0, т.е. 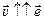 (рис. 9.12). В площадку попадут только те частицы, которые находятся от площадки не дальше, чем υDt (остальные не успеют долететь). Объем, в котором содержатся частицы, которые пересекут площадку, – это объем прямоугольного параллелепипеда с основанием S и высотой υDt: V = sυDt. А число частиц в этом объеме
(рис. 9.12). В площадку попадут только те частицы, которые находятся от площадки не дальше, чем υDt (остальные не успеют долететь). Объем, в котором содержатся частицы, которые пересекут площадку, – это объем прямоугольного параллелепипеда с основанием S и высотой υDt: V = sυDt. А число частиц в этом объеме
N = nV = nsυDt . (9.7)
Потоком частиц Ф называется величина, численно равная числу частиц, пересекающих площадку единичной площади, расположенную так, что ее плоскость перпендикулярна направлению скорости частиц, в единицу времени.
Тогда согласно (9.7) 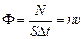 ,
, 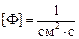 . Запомним:
. Запомним:
Ф = nυ. (9.8)
 Пусть нормаль
Пусть нормаль 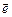 составляет с вектором
составляет с вектором 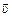 угол a и пусть а и b – длины сторон прямоугольной площадки. Ясно, что S = ab.
угол a и пусть а и b – длины сторон прямоугольной площадки. Ясно, что S = ab.
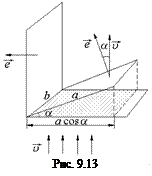
В площадку попадут только частицы, пересекающие проекцию площадки на горизонтальную плоскость (рис. 9.13). Площадь этой проекции S¢ = abcosa.
В этом случае объем, в котором будут находиться частицы, пересекающие площадку за время Dt, будет равен
V¢ = abcosa×υDt = Scosa×υDt,
а число частиц
N¢ = V¢n = ScosaυDtn = пυSDtcosa
или
N¢ = ФSDtcosa. (9.9)
Заметим, что если a = 90°, то N¢ = 0, так как частицы будут лететь параллельно площадке.
Задача 9.5. Сколько капель воды попадет в неподвижное ведро с площадью сечения S = 400 см2 за время Dt = 1,0 с, если скорость капель υ = 10 м/с, а их концентрация п = 1,0 (1/см3). Капли движутся перпендикулярно к плоскости сечения ведра.
| S = 400 см2 Dt = 1,0 с υ = 10 м/с = 1,0×103 см/с п = 1,0 (1/см3) | Решение. Согласно формулам (9.8) и (9.9) N = ФSDt = пυSDt = = 1,0 (1/см3) ×1,0×103 см/с × 400 см2 × 1,0 с » » 4,0×105 (капель). Ответ: N = пSυDt » 4,0×105 (капель). |
| N = ? |
СТОП! Решите самостоятельно: В8, В19, С11.
Дата добавления: 2016-04-11; просмотров: 956;
