III. СКОРОСТЬ ЗВУКОВОГО ИМПУЛЬСА В ГАЗЕ

Газы обладают упругостью сжатия, поэтому в них могут распространяться продольные волны, фазовая скорость которых определяется формулой

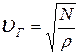
где N – модуль упругости для газа, 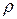- плотность газа.

При деформации сжатия частицы среды движутся в том же направлении, вдоль которого передаётся импульс. В этом случае относитель­ное изменение объёма газа 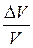равно относительному сжатию (разряжению) 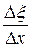и вызывается увеличением или уменьшением давления 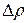, которое играет здесь роль напряжения 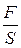в твёрдом теле. Поэтому выражение (5), в данном случае нужно записать следую­щим образом:

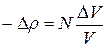
и модуль N, следовательно, выразится отношением:

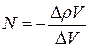
Знак "минус" указывает на то, что с ростом давления объём газа, уменьшается.

Теперь выражение для скорости импульса в газе будет иметь вид:

.

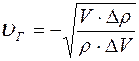Предполагая зависимость между давлением газа в импульсе и его объёмом адиабатической:

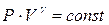
где 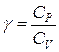и вычисляя полный дифференциал этого выражения, получим:

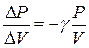и .

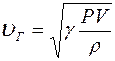Так как плотность газа

,

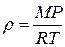то для скорости звукового импульса в газе получим:

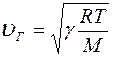, (12)

где R - газовая постоянная (R = 8,31 Дж/моль·К), Т – абсолютная температура газа, М - молярная масса газа, 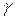- показатель адиабаты.

IV. СТОЯЧИЕ ВОЛНЫ

Если в среде распространяется несколько волн, то колебаний частиц среды оказывается гёометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не передовая возмущение друг другу. Это утверждение называется принципом суперпозиции (наложения) волн. В случае, когда колебания, обусловленные отдельными волнами в каждой точке среды, имеют одинаковую частоту и обладают постоянной разностью фаз, волны называют, когерентными. При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в этом случае; колебательный процесс навивается стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отражённая вол­на, накладываясь друг на друга, дают стоячую волну. Выберем начальные условия так, чтобы уравнения двух плоских волн, распространяющихся вдоль, оси x в противоположных направлениях, имели вид:

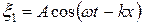и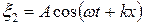

Сложив вместе эти уравнения и преобразовав результат по форму­ле для суммы косинусов, получим

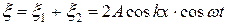. (13)

Уравнение (13) есть уравнение стоячей волны. Из этого уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причём амплитуда зависит от x:

.

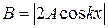В точках, координаты которых удовлетворяют условию

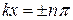, (14)

где n = 0, 1, 2, 3, 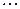, амплитуда колебаний. Достигает максимального значения. Эти точки называются пучностями стоячей волны. Подставляя в условие (14) 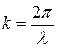, получим значение координат пучностей

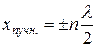(n = 0, 1, 2, 3, 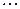). (15)

В точках, координаты которых удовлетворяют условию

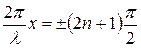(n = 0, 1, 2, 3, ),

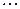амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колеба­ний не совершают. Координаты узлов смеют значения

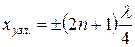(n = 0, 1, 2, 3, 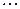). (16)

Узел, как и пучность, представляет собой не одну точку, а плоскость, точки которой имеют значения координаты x, определяемые формулами (15) и (16).

Из этих формул следует, что расстояние между соседними пучнос­тями, так же как и расстояние между соседними узлами, равно 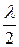. Пучности и узлы сдвинуты друг относительно друга на четверть дли­ны волны.

Обратимся снова к уравнению (13). Множитель 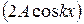при
переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на 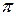. Это означает, что точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключённые между двумя соседними узлами, колеблются синфазно (т.е. в одинаковой фазе).

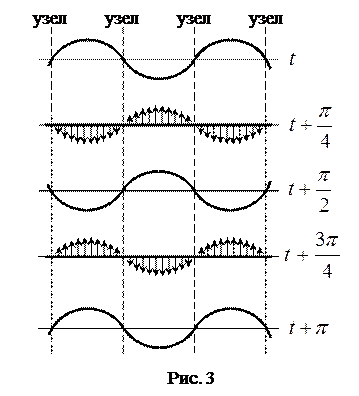На рисунке 3 дан ряд «моментальных фотографий» отклонений точек от положения равновесия. Стрелками показаны скорости частиц. Таким образом, в случае бегущей волны точки среды, лежащие в плоскостях с различными координатами x колеблются с одинаковой амплитудой, но в различных фазах. В случае же стоячей волны в одинаковой фазе, но с различными амплитудами.

В стоячей волне, в отличие от бегущей волны, не происходит течения энергии, т.к. стоячая волна есть результат сложения двух бегущих волн равной амплитуды, распространяющихся в противоположные стороны.

Обе бегущие волны несут с собой одинаковую энергию в противоположных направлениях. Поэтому результирующая стоячая волна не переносит энергии.