II. СКОРОСТЬ УПРУГИХ ВОЛН В ТОНКОМ СТЕРЖНЕ

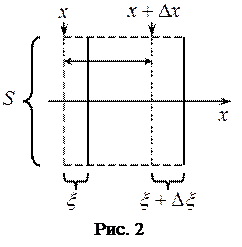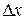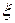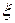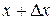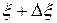Пусть в направлении оси x распространяется продольная плоская волна. Выделим в среде цилиндрический объём с площадью оснований S и высотой (рис. 2). Смещения частиц на разные величины x в каждый момент времени оказываются различными (рис. 1). Если основание цилиндра с координатой x имеет в некоторый момент времени смещение , то смещение оснований с координатой будет . Поэтому рассматриваемый объём деформируется - он полу­чает удлинение 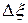, ( 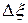- алгебраическая величина, при 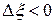соответствует сжатию цилиндра) или относительное удлинение 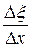. Величина 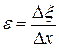даёт среднюю деформацию цилиндра.

Наличие деформации растяжения (сжатия) свидетельствует о существовании нормального напряжения 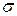, при малых деформациях пропорционального величине деформации. По закону Гука

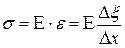, (5)

где 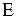- модуль Юнга среды. Продольная волна состоит из чередующихся разряжений и сгущений среды. Скорость распространения импульса деформации и есть скорость волны.

Масса цилиндрического объёма при отсутствии деформации:

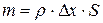, (6)

где 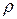- плотность среды. При распространении деформации в стержне движется только «уплотнение» («разряжение»), масса же деформированного объёма так же m:

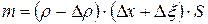. (7)

Здесь 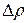- изменение плотности вещества ( 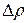- величина алгебраическая, 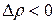. соответствует деформаций растяжения). Соотношения (6) и (7) приравняем:

.

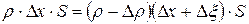После преобразования, учитывая, что 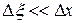и ,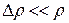

получим:

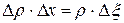
или

.

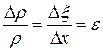Тогда

. (8)

При распространении деформации это «уплотнение» 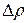последовательно передается от слоя к слою со скоростью 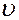. Дело обстоит, таким образом, как если бы импульс деформации обладал массой

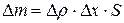
и количеством движения

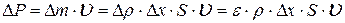. (9)

Рассмотрим промежуток времени 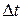, за который импульс дефор­мации распространяется на расстояние, равное высоте цилиндра. Тогда 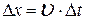и равенство (9) запишется в виде

.

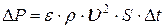Таким образом, за время 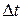через основание цилиндра S слева направо пройдет количество движения 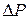и на такую же величину возрастёт количество движения справа от рассматриваемого сечения. Скорость изменения количества движения

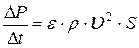. (10)

По второму закону Ньютона она должна быть равна силе, действую­щей на это сечение слева направо и вызывающей деформацию. Тогда, с учётом равенств (5) и (10), получим:

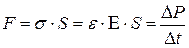
или

.

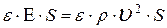Отсюда

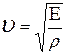. (11)

Аналогичные вычисления для поперечных волн приводят к выражению

,

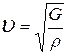где G - модуль сдвига.