ПОД УГЛОМ К ГОРИЗОНТУ
Как мы уже знаем, мгновенным ускорением 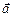 (или просто ускорением) называется векторная величина
(или просто ускорением) называется векторная величина 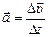 при Dt ® 0, где
при Dt ® 0, где 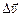 – изменение вектора скорости за время Dt.
– изменение вектора скорости за время Dt.
Движение, при котором мгновенное ускорение постоянно 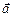 = =
= = 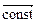 , называется равнопеременным.
, называется равнопеременным.
Пусть тело движется из точки, определяемой радиусом-вектором 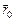 с начальной скоростью
с начальной скоростью 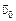 и с постоянным ускорением
и с постоянным ускорением 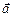 , пусть начальный момент времени равен t0, тогда
, пусть начальный момент времени равен t0, тогда
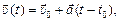 (10.1)
(10.1)
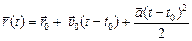 . (10.2)
. (10.2)
В координатной форме уравнения (10.1) и (10.2) имеют вид
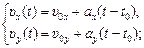 (10.3)
(10.3)
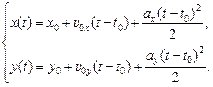 (10.4)
(10.4)
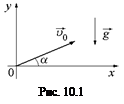
Пусть тело брошено под углом a к горизонту с начальной скоростью υ0 (рис. 10.1). Тогда справедливы соотношения:
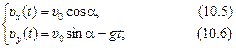
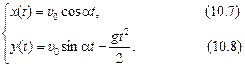
Время подъема тела tп находится из условия
υу(tп) = 0 Þ υ0sina – gtп = 0 Þ
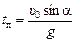 . (10.9)
. (10.9)
Время полета тела tпол находится из условия
у (tпол) = 0 Þ υ0sinatпол – 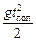 = 0 Þ
= 0 Þ
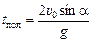 . (10.10)
. (10.10)
Высота подъема Н находится из условия
Н = у(tп) Þ
Н = υ0sinatп – 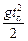 = υ0sina
= υ0sina 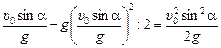 ,
,
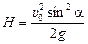 . (10.11)
. (10.11)
Дальность полета L находится из условия
L = x(tпол) Þ 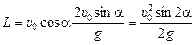 ,
,
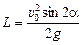 . (10.12)
. (10.12)
Если из (10.7) выразить t через х и подставить в (10.8), получим уравнение траектории у = у(х):
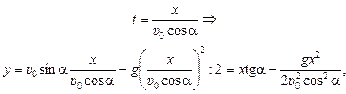
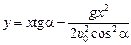 . (10.13)
. (10.13)
Задача 10.1. Тело брошено под углом a к горизонту с начальной скоростью υ0. Определить зависимость модуля скорости от времени υ(t), а также зависимость угла между вектором скорости и горизонтальной осью х: b(t).
| υ0 a | Решение. Согласно формулам (10.5) и (10.6)
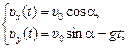
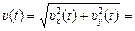 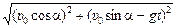 . .
| |
| b(t) = ? υ(t) = ? | ||
Из DО¢А¢В¢ (рис. 10.2):
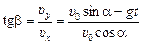 ; ;
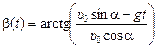 . .
| 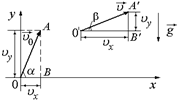 Рис. 10.2
Рис. 10.2
| |
Ответ: 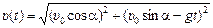 ;
;
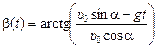 .
.
СТОП! Решите самостоятельно: В1, В2, С1.
Задача 10.2. Мотоциклист въезжает на высокий берег рва (рис. 10.3,а). Какую минимальную скорость должен иметь мотоциклист в момент отрыва от берега, чтобы перескочить ров?
| a s h | а) 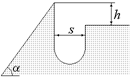 б) б) 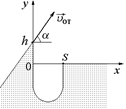 Рис. 10.3
Рис. 10.3
|
| υотр = ? | |
Решение. Запишем уравнение движения мотоциклиста после отрыва от берега в проекциях на оси х и у (рис. 10.3,б):
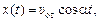
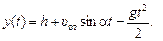
В момент приземления τ: х(τ) = s, у(τ) = 0. Отсюда
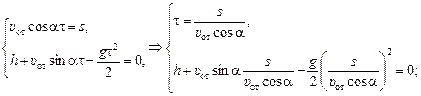
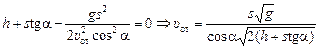 .
.
Ответ: 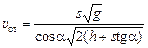 .
.
СТОП! Решите самостоятельно: В5, В6, С3.
Задача 10.3. С высоты Н на наклонную плоскость, образующую угол a с горизонтом, свободно падает мяч и упруго отражается. Определите расстояния между местами 1-го и 2-го, 2-го и 3-го, …, п-го и п+1-го ударов о плоскость.
| Н a | Решение. Введем с.о. х0у, такую, чтобы ось х была параллельна наклонной плоскости (рис. 10.4). 1. Пусть при ударе о наклонную плоскость скорость мяча равна υ0, тогда | 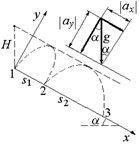 Рис. 10.4
Рис. 10.4
| |
| s12 = ? s23 = ? sn,n+1 =? | |||
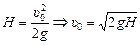 .
2. При ударе величина υх сохраняется, а υу меняет знак (рис. 10.5). Величина скорости υ0 при ударе не меняется.
3. Из рис. 10.4 видно, что ах = gsina, ay = –gcosa.
4. Из рис. 10.5 видно, что после удара .
2. При ударе величина υх сохраняется, а υу меняет знак (рис. 10.5). Величина скорости υ0 при ударе не меняется.
3. Из рис. 10.4 видно, что ах = gsina, ay = –gcosa.
4. Из рис. 10.5 видно, что после удара
| |||
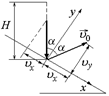 Рис. 10.5
Рис. 10.5
|
υ0х = υ0sina, υ0y = υ0cosa.
5. Тогда согласно формулам (10.3) и (10.4)
υy(t) = υ0cosa – gcosat, (1)
y(t) = υ0cosat – 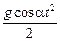 (2)
(2)
(за начало движения принят момент первого удара).
6. В момент t0 второго удара
y(t) = 0 Þ υ0cosat0 – 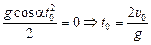 ,
,
υу(t0) = υ0cosa – gcosa 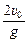 = – υ0cosa.
= – υ0cosa.
7. Сразу же после удара скорость υy меняет знак и становится равной +υ0cosa, т.е. такой же, как в момент после первого удара о наклонную плоскость!
8. Поскольку после второго удара значения υy и ау будут точно такими же, как после первого удара, уравнения (1) и (2) не изменятся. Следовательно, время и между первым и вторым ударами, и между двумя последовательными ударами одно и то же и равно
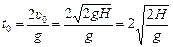 .
.
9. Найдем координату хп п-го удара мяча о наклонную плоскость. Пусть 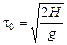 – время падения мяча из начального положения на наклонную плоскость. Тогда
– время падения мяча из начального положения на наклонную плоскость. Тогда 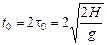 – время между двумя последовательными ударами. Отсюда время tп от начала движения до п-го удара равно
– время между двумя последовательными ударами. Отсюда время tп от начала движения до п-го удара равно
tn = τ0 + (n – 1)t0 = τ0 + (n – 1)×2τ0 = τ0(2п –1).
Время tn+1 от начала движения до (п + 1)-го удара tn+1 = tп + 2t0 = = t0(2п + 1).
Координата п-го удара хп равна
хп = х(tп) = 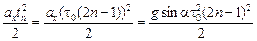 .
.
(Если за начало отсчета времени взять начало падения мяча, то υ0х = 0, а зависимость х(t) имеет вид 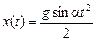 .)
.)
10. Расстояние sn,n+1 между п-м и (п+1)-м ударами равно
sn,n+1 = хп+1 – хп = 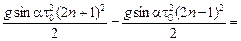
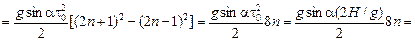
= 8пHsina.
11. Тогда s12 = 8×1×H×sina = 8Hsina, s23 = 8×2×H×sina = 16Hsina.
Ответ: s12 = 8Hsina; s23 = 16Hsina; sn,n+1 = 8пHsina.
СТОП! Решите самостоятельно: В7, В9, С8.
Задача 10.4. Цель, находящаяся на холме, видна с места расположения орудия под углом a к горизонту. Дистанция (расстояние по горизонтали от орудия до цели) равна L. Стрельба по цели производится при угле возвышения b (рис. 10.6,а). Определить начальную скорость υ0 снаряда, попадающего в цель. Сопротивление воздуха не учитывать.
| a, L, b | 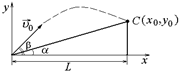 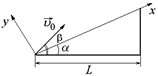 а) б)
Рис. 10.6
а) б)
Рис. 10.6
|
| υ0 - ? | |
Решение. Задачу можно решать по-разному. Можно выбрать координатные оси, как показано на рис. 10.6,а, тогда условие попадания в цель х(tп) = L, y(tп) = Ltga.
Можно выбрать с.о., какпоказано на рис. 10.6,б, тогда условием попадания в цель будет х(tп) = 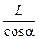 , y(tп) = 0.
, y(tп) = 0.
Можно воспользоваться уравнением траектории у(х) (10.13):
у = хtgb – 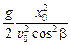 .
.
В момент падения снаряда x = L; y = Ltga (рис. 10.6,а), тогда
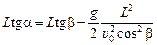
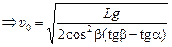 .
.
Ответ: 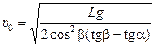 .
.
СТОП! Решите самостоятельно: В8, В10.
Задача 10.5.На некоторой высоте снаряд разорвался на два осколка, которые получили скорости 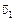 и
и 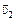 соответственно (рис. 10.7,а). Пренебрегая сопротивлением воздуха, определите, как будут двигаться осколки друг относительно друга. На каком расстоянии L будут находиться осколки друг от друга через время τ?
соответственно (рис. 10.7,а). Пренебрегая сопротивлением воздуха, определите, как будут двигаться осколки друг относительно друга. На каком расстоянии L будут находиться осколки друг от друга через время τ?
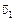 , , 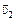 , τ , τ
| а)  б) б) 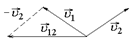 Рис. 10.7
Рис. 10.7
|
| L = ? | |
Решение.Найдем скорость 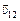 первого осколка относительно второго:
первого осколка относительно второго: 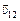 =
= 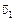 –
– 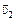 (рис. 10.7,б). При этом согласно формуле (10.1)
(рис. 10.7,б). При этом согласно формуле (10.1) 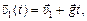
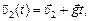 тогда
тогда
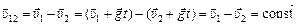 ,
,
т.е. не зависит от времени.
Это значит, что первый осколок относительно второго движется равномерно и прямолинейно со скоростью 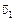 –
– 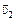 ! Тогда расстояние между осколками через время τ будет равно s = |
! Тогда расстояние между осколками через время τ будет равно s = | 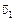 –
– 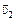 |t.
|t.
Ответ: s = | 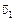 –
– 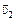 |t.
|t.
СТОП! Решите самостоятельно: А2, А3, В13, С13.
Задача 10.6. Из точки А, находящейся над поверхностью земли на высоте h = 5 м (точно), свободно падает тело. Одновременно из точки В, находящейся на расстоянии l = 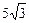 м (точно) по горизонтали от точки А, под углом a к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Определить угол a.
м (точно) по горизонтали от точки А, под углом a к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Определить угол a.
h = 5 м
l = 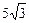 м м
| Решение. Читатель. Ну, здесь ход решения более-менее ясен. Нужно записать уравнения движения: x = x(t) и у = у(t) для каждого тела, приравнять координаты тел в момент встречи: х1(tв) = x2(tв), у1(tв) = у2(tв), решить полученную систему уравнений... |
| a = ? | |
Автор: (перебивая). А давайте по-другому! Примем ПЕРВОЕ тело за неподвижное и найдем скорость ВТОРОГО тела относительно ПЕРВОГО в момент начала движения: 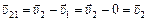 . А так как эта скорость не зависит от времени (см. задачу 10.5), то второе тело относительно первого движется вдоль отрезка ВА (рис. 10.8). Значит, для того чтобы ВТОРОЕ тело столкнулось в воздухе с ПЕРВЫМ телом, необходимо, чтобы вектор
. А так как эта скорость не зависит от времени (см. задачу 10.5), то второе тело относительно первого движется вдоль отрезка ВА (рис. 10.8). Значит, для того чтобы ВТОРОЕ тело столкнулось в воздухе с ПЕРВЫМ телом, необходимо, чтобы вектор 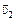 совпадал с прямой ВА. Тогда из треугольника ABC имеем:
совпадал с прямой ВА. Тогда из треугольника ABC имеем:
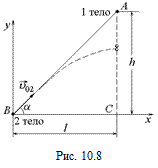
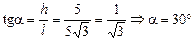 .
.
Читатель: Здорово, конечно, но как-то дико: с одной стороны, траектория второго тела ПАРАБОЛА, а с другой стороны – ПРЯМАЯ. Но не может же тело одновременно двигаться и по параболе, и по прямой!
Автор: В том-то и дело, что может! Представьте себе, что у нас имеется большой вертикально расположенный лист бумаги, на котором ВТОРОЕ тело, двигаясь по направлению к ПЕРВОМУ телу, чертит свою траекторию. Если лист неподвижен относительно земли, то будет начерчена парабола, но если лист будет свободно падать, оставаясь при этом неподвижным относительно ПЕРВОГО тела, то на этом падающем листе ВТОРОЕ тело начертит ПРЯМУЮ! Удивительно, но факт. Не верите – проверьте экспериментально!
СТОП! Решите самостоятельно: В15, В16, С11, С12.
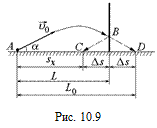 Задача 10.7. Футбольному мячу придали начальную скорость υ0 = 20 м/с, направленную под углом a = 15° к горизонту. На расстоянии L = 15 м от точки вылета мяча с поверхности земли находится стенка, о которую мяч ударяется абсолютно упруго: угол отскока равен углу падения, а скорость до удара равна скорости после удара (рис. 10.9). Каково расстояние sx от точки удара до точки его приземления?
Задача 10.7. Футбольному мячу придали начальную скорость υ0 = 20 м/с, направленную под углом a = 15° к горизонту. На расстоянии L = 15 м от точки вылета мяча с поверхности земли находится стенка, о которую мяч ударяется абсолютно упруго: угол отскока равен углу падения, а скорость до удара равна скорости после удара (рис. 10.9). Каково расстояние sx от точки удара до точки его приземления?
| υ0 = 20 м/с a = 15° L = 15 м | Решение. Если бы стенки не было, то дальность полета была бы равна
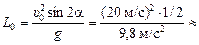 20 м >L = 15 м. 20 м >L = 15 м.
|
| sx = ? |
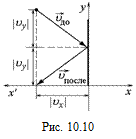 Значит, мяч ударится о стенку. В момент удара вертикальная проекция скорости сохранится, а горизонтальная поменяет знак (рис. 10.10):
Значит, мяч ударится о стенку. В момент удара вертикальная проекция скорости сохранится, а горизонтальная поменяет знак (рис. 10.10): 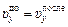 ,
, 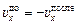 .
.
Введем с.о. х¢0у, в которой ось 0х¢ противоположна оси 0х. В этой новой системе υх сохраняет и свою величину, и свой знак. Следовательно, скорость 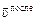 в этой с.о. точно такая же, как
в этой с.о. точно такая же, как 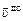 в старой с.о., т.е. мяч в новой с.о. движется так же, как если бы на его пути не было стенки. А это значит, что траектория мяча после удара будет симметрична относительно оси у траектории мяча, который пролетел бы «сквозь» стенку.
в старой с.о., т.е. мяч в новой с.о. движется так же, как если бы на его пути не было стенки. А это значит, что траектория мяча после удара будет симметрична относительно оси у траектории мяча, который пролетел бы «сквозь» стенку.
Тогда, как видно из рис. 10.9, Ds = L0 – L,
sx = L0 – 2Ds = L0 – 2(L0 – L) = 2L – L0 = 2×15 м – 20 м = 10 м.
Ответ: sx =2L – L0 = 10 м.
СТОП! Решите самостоятельно: В17, В18, С16, С17.
Дата добавления: 2016-04-11; просмотров: 4755;
