Дифракция плоской волны на круглом отверстии
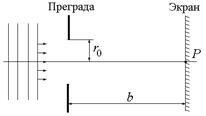Рис. 20.20
|
Пусть на круглое отверстие падает плоская волна (рис. 20.20). Выясним, что при этом будет наблюдаться на экране.
В данном случае все будет почти так же, как и в случае сферических волн, только немного проще. Плоскую волну можно рассмотреть как частный случай сферической волны, радиус которой а ® ¥. Тогда площадь одной (произвольной) зоны Френеля можно найти по формуле (20.4), устремив а к бесконечности:
.
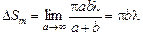Запомним:
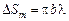. (20.12)
Аналогично с помощью формулы (20.5) можно найти радиус т-й зоны:
.
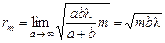Запомним:
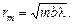(20.13)
Задача 20.1.На диафрагму с диаметром отверстия D = 1,96 мм падает нормально параллельный пучок монохроматического света (l = 600 нм). При каком наибольшем расстоянии b между диафрагмой и экраном в центре дифракционной картины еще будет наблюдаться темное пятно?
| D = 1,96 мм l = 600 нм | Решение. Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон четное, то в центре дифракционной картинки будет темное |
| bmax = ? | |
пятно. Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. В самом деле, по формуле (20.13) чем больше b, тем больше радиус т-й зоны.
Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля. Радиус диафрагмы должен равняться радиусу второй зоны, т. е.
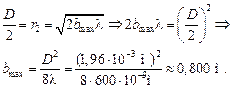
Ответ: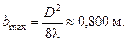 
СТОП! Решите самостоятельно: В3–В6.
Дата добавления: 2016-04-11; просмотров: 1626;