Дифракция от круглого диска
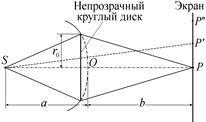Рис. 20.18
|
Поместим между источником света S и точкой наблюдения Р непрозрачный диск радиуса r0 (рис. 20.18). Если диск закроет т первых зон Френеля, то амплитуда в точке Р будет равна:
А = Ат+1 – Ат+2 + Ат+3 – … =
= 
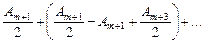
Выражения, стоящие в скобках, можно положить равными нулю, следовательно:
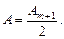(20.11)
Рис. 20.19
|
Что же получится на экране? При малых т Ат+1 примерно такая же, как А1. Поэтому освещенность в точке Р почти такая же, как при отсутствии преграды!
По мере удаления от точки Р в точках Р¢ и Р¢¢ (см. рис. 20.18), максимумы и минимумы амплитуды будут чередоваться (рис. 20.19).
Светлое пятнышко в центре тени, отбрасываемой диском, послужило причиной инцидента, происшедшего между Пуассоном[1] и Френелем. Парижская академия наук предложила дифракцию света в качестве темы на премию за 1818 г. Френелем была представлена работа, в которой все известные к тому времени оптические явления объяснялись с волновой точки зрения. Рассматривая эту работу, Пуассон, бывший членом конкурсной комиссии, обратил внимание на то, что из теории Френеля вытекает «нелепый» вывод: в центре тени, отбрасываемой небольшим круглым диском, должно находиться светлое пятно. Араго[2] тут же произвел опыт и обнаружил, что такое пятно действительно имеется. Это принесло победу и всеобщее признание волновой теории света.
СТОП! Решите самостоятельно: А1, В1, В2, С1–С3.
Дата добавления: 2016-04-11; просмотров: 794;