Дифракция от круглого отверстия

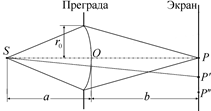Рис. 20.14

Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиусом r₀ (рис. 20.14). Расположим экран так, чтобы перпендикуляр, опущенный на экран из источника света S попал в центр отверстия – точку О. Попробуем выяснить, какой будет освещенность в точках наблюдения Р, Р¢, Р¢¢.

Читатель: А как связана освещенность с амплитудой колебаний световой волны А? И вообще, какой физический смысл имеет величина А?

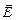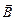Автор: Мы уже говорили, что световая волна – это электромагнитная волна. В ней совершают колебания векторы и (напряженность электрического поля и магнитная индукция), причем фазы этих колебаний равны.

Установлено, что зрительные ощущения вызывает именно вектор 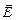. А мы уже установили в курсе электростатики, что плотность энергии электрического поля пропорциональна Е². Поэтому в нашем случае можно считать, что освещенность I (т.е. количество световой энергии, падающей на единицу поверхности) в каждой точке пропорционально квадрату амплитуды световой волны I ~ A².

Сначала рассмотрим ситуацию в точке Р. Пусть в отверстии «укладывается» целое число зон Френеля, т.е. 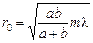, где т = 1, 2, 3… В соответствии с равенством (20.7) амплитуда колебания в точке Р будет равна

А = А₁ – А₂ + А₃ – А₄ + … +А_т, (20.10)

где перед А_т стоит знак «плюс», если т – нечетное, и знак «минус», если т – четное:

если т = 1, то А = А₁;

если т = 2, то А = (А₁ – А₂) » 0;

если т = 3, то А = (А₁ – А₂ + А₃) » А₁;

если т = 4, то А = (А₁ – А₂) + (А₃ – А₄) » 0 и т.д.

При очень большом т, когда открыты почти все зоны, мы в соответствии с формулой (20.8) получим 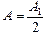. Таким образом, если открыто четное число зон А » 0, а если нечетное – А » А₁ (если число зон не очень велико). Соответственно, освещенность в точке Р при нечетном числе зон в 4 раза (!) больше, чем при отсутствии экрана вообще (т.е. когда открыты все зоны).

Читатель: А как определить освещенность в точках Р¢ и Р¢¢ (см. рис. 20.14)?

Автор: Допустим, что для точки Р «открыты» три зоны Френеля (рис. 20.15, а). Сместимся на экране в точку Р¢ (рис. 20.16, а). При этом ближайшая к точке Р¢ точка световой волны О¢ окажется ниже, чем ближайшая к точке Р точка световой волны О. Поэтому изменится и расположение зон Френеля. Останутся открытыми зоны 1 и 2, зона 3 частично исчезнет из «поля зрения» точки Р¢ и добавится немного зоны 4 (рис. 20.15, б). Поэтому амплитуда в точке Р¢ будет меньше, чем в точке Р. В самом деле, мы «убавили» светлой (нечетной) зоны и «добавили» темной (четной) зоны.

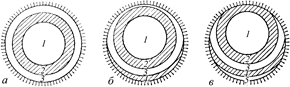Рис. 20.15

а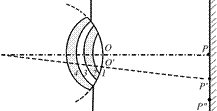

б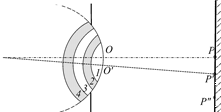

в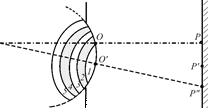

Рис. 20.16

В точке Р¢¢ (рис. 20.16, в) немного убавится темная зона 2, заметно прибавится светлая зона 3 и появится немного светлой зоны 5. Правда, немного возрастет и темная зона 4 (см. рис. 20.15, в). Но в целом по сравнению с точкой Р¢, должно быть светлее. Таким образом, перемещаясь в сторону от точки Р по экрану мы должны увидеть чередование темных и светлых колец (рис. 20.17).

Нечетное т Четное т Рис. 20.17

Читатель: У меня вопрос. Если размер отверстия сделать достаточно большим, то мы должны увидеть светлое пятно безо всяких там светлых и темных колец, т.е. по мере увеличения отверстия картина должна как бы размываться. Как это согласовать с теорией Френеля?

Автор: Если открыты все зоны, то амплитуда в точке Р равна А/2. Если мы сместимся в точку Р¢ (см. рис. 20.16, б), то и в точке Р¢ будут открыты практически все зоны. Поэтому и там результирующая амплитуда будет точно такой же – А/2.