Динамические напряжения в диске постоянной толщины без центрального отверстия
Динамические напряжения определяются при следующих условиях:
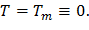

Первое граничное условие из (19) означает, что в центре диска без центрального отверстия радиальное и окружное напряжения совпадают, из-за того, что исчезает различие между окружным и радиальным напряжениями.
Применим (19) к общим решениям (16) и (18). При r=0 имеем
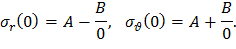
Радиальные и окружные напряжения должны иметь конечные значения в центре диска при r=0, следовательно, параметр B равен нулю:

Подстановка второго граничного условия из (19) в общее решение (16) с учетом (20) даст
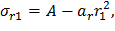
откуда можно выразить постоянную A:

Таким образом, распределение радиальных динамических напряжений в диске постоянной толщины без центрального отверстия получим из выражения (16), используя значения постоянных интегрирования в виде (20) и (21):
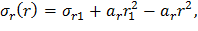
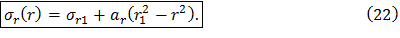
Распределение окружных динамических напряжений в диске постоянной толщины без центрального отверстия находится подстановкой (20) и (21) в общее решение (18):
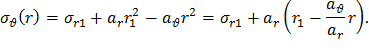
Учитывая формулы (15) и (17) окончательно получим
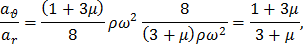
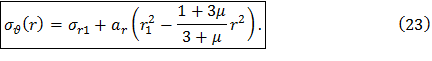
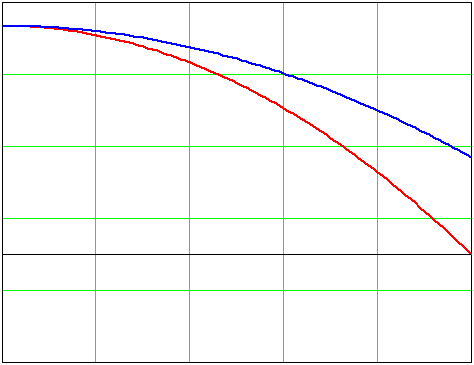
На рис. 9 показаны эпюры динамических напряжений для сплошного диска постоянной толщины.
| σr, σθ |
| r |
| r1 |
| 0 |
| σr1 |
| ar r12 |
| Рис. 9. Распределение напряжений в сплошном диске постоянной толщины |
| σθ |
| σr |
Таким образом, максимальные значения радиальных и окружных динамических напряжений достигаются в центре диска.
Дата добавления: 2016-02-16; просмотров: 1009;
