Распределение напряжений в тонком вращающемся неравномерно нагретом диске постоянной толщины

Полагая h=const, из уравнения равновесия (4) получим

Применяя правило дифференцирования произведения, имеем

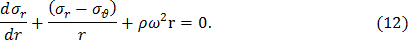
Уравнение равновесия (12) для диска постоянной толщины используем для исключения четвертого слагаемого в уравнении (9), что позволит легко его проинтегрировать. Для этого умножим (12) на 1+μ и сложим с (9):

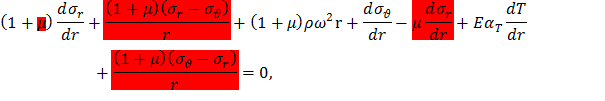
В полученном уравнении разделим переменные и проинтегрируем, воспользовавшись правилом суммирования производных,

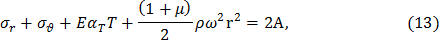
где 2A – постоянная интегрирования.

Уравнение равновесия в форме (12) содержит обе неизвестные величины σ_r и σ_θ. Исключим из него σ_θ, применив общее решение (13). С этой целью разделим (13) на r и сложим с (12):

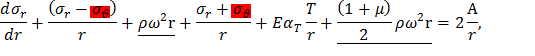
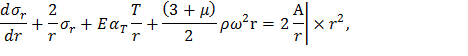
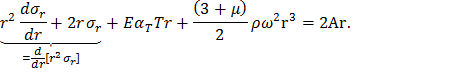
В последнем уравнении разделим переменные и проинтегрируем

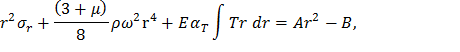
где B – постоянная интегрирования. Выразив из последнего соотношения σ_r, получим

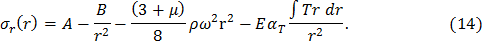
Обозначим

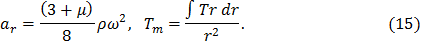
Подставив введенные обозначения (15) в (14), окончательно получим общее решение для распределения радиальных напряжений в диске постоянной толщины:

Теперь из уравнения (13), учитывая (16), находим и σ_θ:

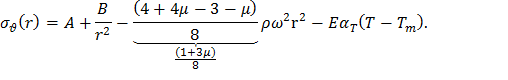
Обозначив,

окончательно получим общее решение для распределения окружных напряжений в диске постоянной толщины

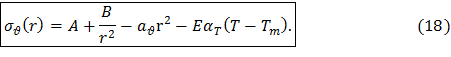
Постоянные интегрирования A и B должны быть найдены из граничных условий (10) на периферии и расточке диска.

Вследствие линейности задачи полные напряжения в диске равны алгебраической сумме динамических и температурных напряжений, поэтому рассматривать их будем по отдельности.