Динамические напряжения в диске постоянной толщины с центральным отверстием
Пусть T=Tm≡0, а радиальные напряжения на периферии и расточке диска соответствуют условиям (10). Подчиняя общее решение (16) этим условиям, получаем
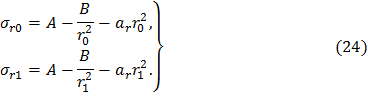
Полученная система из двух алгебраических уравнений включает две неизвестных величины A и B. Для определения B вычтем из первого уравнение второе:
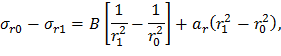
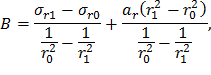
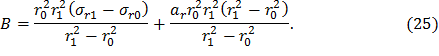
Выражение для A получим из первого уравнения системы (24), используя формулу (25):


Подставив соотношения (25) и (26) для параметров A и B в общее решение (16), получим
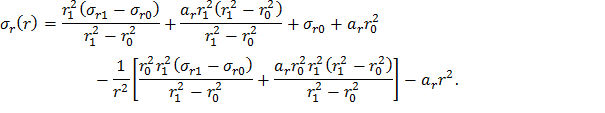
Сгруппируем слагаемые, содержащие σr1, σr0 и ar, в комплексы S1(r), S2(r) и S3(r) соответственно, а функцию σr(r) представим как
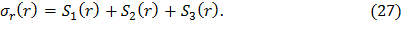
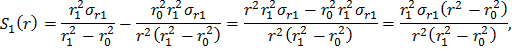

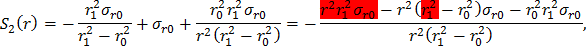

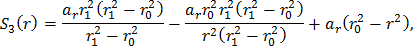

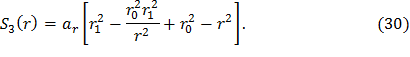
Подставив выражения (28), (29) и (30) в формулу (27), получим распределение радиальных динамических напряжений в диске постоянной толщины с центральным отверстием:
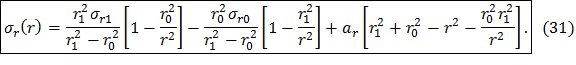
Распределение окружных динамических напряжений в диске постоянной толщины с центральным отверстием получим, выполнив подстановку соотношений (25) и (26) в общее решение (18):

Первые слагаемые в формулах (31) и (32) соответствуют напряжениям от периферийной нагрузки, вторые слагаемые соответствуют напряжениям от нагрузки на расточке диска, третьи слагаемые соответствуют напряжениям в свободно вращающемся диске без краевых нагрузок.
| r1 |
| r0 |
| σr |
| σϑ |
| σϑ |
| σr |
| σϑmax |
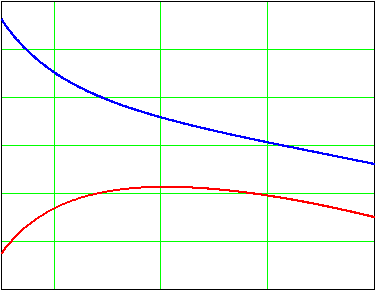
| Рис. 10. Распределение напряжений в диске с центральным отверстием |
Типичные эпюры напряжений в диске с отверстием представлены на рис. 10. Очевидно, что максимальными будут окружные напряжения на расточке диска. Вычислим их, подставив значение r=r0 в соотношение (32),


Обозначим α=r0/r1 и q0=-σr. Тогда
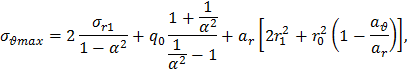
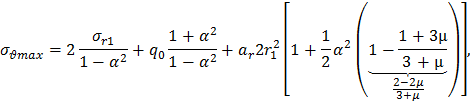

При увеличении r0 возрастает α и все три слагаемых в формуле (33), следовательно, растёт значение σθmax.
Сравним максимальное окружное напряжение σ’’θmax в диске с малым центральным отверстием при q0 =0 с окружным напряжением σ’θmax в центре сплошного диска. При условии, что для малого отверстия α<<1 из формулы (33) имеем

Окружное напряжение в центре сплошного диска получаем из соотношения (23) при r=0:

Из уравнений (34) и (35) следует

то есть центральное отверстие малого диаметра в сплошном диске приводит к увеличению максимального окружного напряжения в 2 раза. Следовательно, малое отверстие в диске является источником концентрации напряжений с коэффициентом концентрации ασ=2.
Дата добавления: 2016-02-16; просмотров: 1021;
