Расчет напряжений в диске произвольного профиля на основе решения для диска постоянной толщины
С помощью цилиндрических сечений разобьем диск произвольного профиля по радиусу на n участков (рис. 14). Будем считать, что в пределах каждого участка толщина диска постоянная.
| r0 |
| r1 |
| 1 |
| 2 |
| 3 |
| s |
| n |
| ∙∙∙ |
| ∙∙∙ |
| rs |
| Рис. 14. Схема разбивки диска произвольного профиля |
Получившийся таким образом диск ступенчатого профиля состоит из участков постоянной толщины, для каждого из которых справедливы общие решения (16) и (18) со своими значениями постоянных интегрирования

где As и Bs – значения постоянных интегрирования для рассматриваемого участка с порядковым номером s (s=1, 2, 3, …, n). Нумерация участков производится от периферии диска.
| σ’r |
| σ’’r |
| h’ |
| h’’ |
| Рис. 15. Сопряжение двух участков диска |
1. Условие равновесия сил, приложенных к бесконечно тонкому слою, включающему стык, то есть

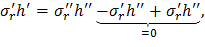
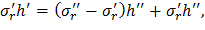
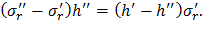
Разделив обе части последнего выражения на h’’, окончательно получим

где σ’r, h’ – радиальное напряжение и толщина диска до скачкообразного изменения толщины; σ’’r, h’’ – то же после скачкообразного изменения толщины.
2. Условие равенства радиальных смещений в месте стыка

где u’ – радиальное смещение до скачкообразного изменения толщины; u’’ – радиальное смещение после скачкообразного изменения толщины. Разделим обе части выражения (67) на радиус стыка r:

Выразим деформации через напряжения, используя закон Гука,
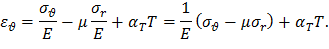
Учитывая, что температурные деформации не могут меняться скачкообразно, имеем
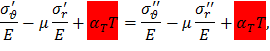


Рассчитать напряжения в диске произвольного профиля можно, применив метод двух расчетов.
Перепишем уравнения (65) следующим образом:

Обозначим выражения, стоящие в левых частях формул (69), соответственно функциями pr(r) и pθ(r), то есть

Тогда с учетом (70) уравнения (69) примут вид:

Первый расчет.
1. Принимается заданное из граничного условия на периферии значение σr1 и произвольное окружное напряжение на периферии σθ1≠0 (любое число).
2. Записываются уравнения (71) при r=r1 и s=1, то есть на периферии диска:

где pr1 и pθ1 – известные числа, полученные по формулам (70) при r=r1.
Выражения (72) представляют собой систему из двух уравнений относительно двух неизвестных A1 и B1. Сложив уравнения (72), получим значение коэффициента A1:

Вычитая из второго уравнения системы (71) первое, определим значение коэффициента B1:
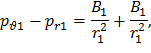

3. По найденным значениям A1 и B1, используя формулы (65), определяются напряжения в любой точке первого участка и, в частности, на его второй границе при r=r2, то есть
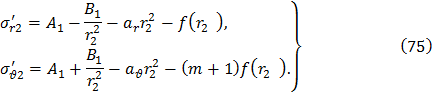
Верхним индексом обозначены значения напряжений до скачкообразного изменения толщины при r=r2.
4. Для определения напряжений после скачкообразного изменения толщины используются формулы (66) и (68):

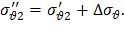
Эти напряжения являются начальными для второго участка. По найденным значениям σ’’r2 и σ’’θ2 определяются pr2 и pθ2 по формулам (70) при r=r2. Далее записывается система уравнений (71) при r=r2 и s=2

из решения которой находятся значения коэффициентов A2 и B2:

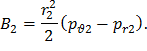
5. Используя значения A2 и B2,по формулам (65) определяются напряжения в любой точке второго участка и, в частности, на его нижней границе при r=r3 и т.д.
В результате по этой методике определяется система напряжений σIr(r) и σIθ(r). Верхний индекс означает напряжения первого расчета. Однако полученные значения не будут удовлетворять граничным условиям на расточке диска при r=r0 (σIr0≠σr0), так как при выполнении первого расчета произвольно принималось значение окружного напряжения на периферии.
Для удовлетворения граничному условию на расточке диска выполняется второй расчет при следующих допущениях: σr1=0; σθ1≠0 (любое число); ω=0; ΔТ=0.
Второй расчет производится по той же самой методике, как и первый, по уравнениям (65) без учета вращения и неравномерного нагрева. В результате определяется система напряжений σIIr(r) и σIIθ(r).
Действительные напряжения вычисляются как

где k – корректирующий множитель.
Напряжения (76) удовлетворяют граничным условиям на периферии диска при любом k. Значение корректирующего множителя определяется исходя из граничных условий на расточке. При условии, что σr(r0)=σr0, имеем
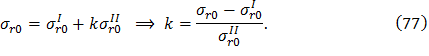
Дата добавления: 2016-02-16; просмотров: 860;
