Расчет дисков, посаженных на вал с натягом
| r0 |
| rд |
| -uв |
| uд |
| rв |
| Рис. 13. Втулка диска перед посадкой его на вал |
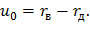
После посадки радиус расточки возрастает на значение смещения uд, а радиус вала уменьшается на значение смещения uв. Таким образом,

Разделим обе части равенства (55) на r0:
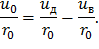
Так как u0<<r0, то r0≈ rв≈ rд. Тогда последнее выражение примет следующий вид:
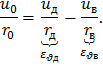
Таким образом,

где εθд – окружная деформация на расточке диска; εθв – окружная деформация на поверхности вала. Если диск и вал находятся в состоянии упругости, то деформации и соответствующие напряжения связаны соотношениями закона Гука:
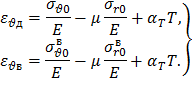
Подставив выражения для окружных деформаций в формулу (56), получим
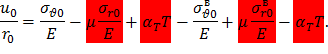
Так как радиальные напряжения на контактной поверхности посадки для вала и диска одинаковы и температурные деформации также равны, то

где σвθ0 – окружное напряжение на поверхности вала; σθ0 –окружное напряжение на расточке диска.
Участок вала будем рассматривать как вращающейся диск с наружным радиусом r0 при постоянной температуре с напряжением в периферийной зоне σвr0, равным контактному напряжению σr0 на расточке диска. Влиянием малого центрального отверстия в вале можно пренебречь. Таким образом, для участка вала применим формулы для расчета напряжений в диске без центрального отверстия (22) и (23). Принимая во внимание введенные обозначения, значение окружного напряжения на поверхности вала определится как
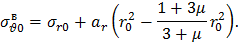
С учетом формулы (15) имеем

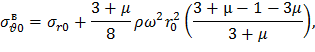
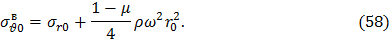
Подставляя последнее выражение в (57), получаем
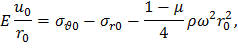

Соотношение (59) представляет собой граничное условие, которому должны удовлетворять напряжения в диске, посаженном на вал с натягом.
Применим условие (59) для расчета дисков постоянной толщины. Радиальные напряжения на расточке диска составляют σr(r0)=σr0=-q, а окружные можно найти по формуле (33), т.е σθ(r0)=σθ0=σθmax. Тогда выражение (59) примет следующий вид:
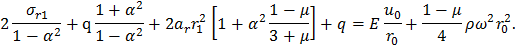
Учитывая формулу (15) имеем
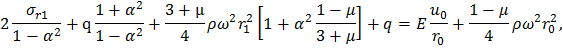
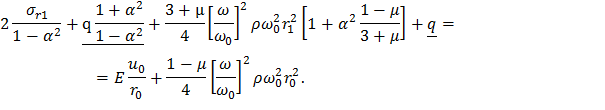
Приведем подобные слагаемые:
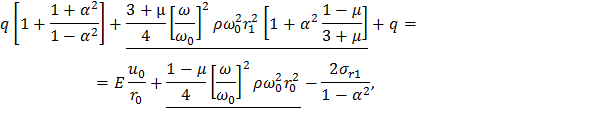
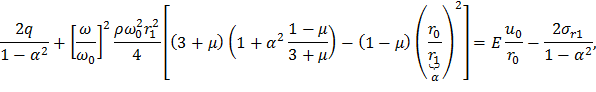
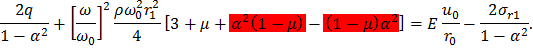
Разделив обе части последнего выражения на 2, окончательно получим

Соотношение (60) связывает между собой контактное давление q, частоту вращения ω и величину натяга u0 при ΔТ=0.
Дата добавления: 2016-02-16; просмотров: 1238;
