Принцип Гюйгенса–Френеля

Дифракция света

Одним из законов геометрической оптики является закон прямолинейного распространения света. До сих пор у нас не было оснований сомневаться в том, что в однородной среде свет распространяется прямолинейно. И вот пришло время усомниться в этом.

Рассмотрим экспериментальные факты.

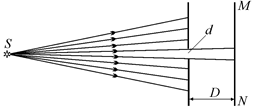
На рис. 20.1, а показан опыт, когда точечный источник S освещает экран, в котором сделано круглое отверстие. За первым экраном находится второй экран MN, на который попадает свет от источника, прошедший через отверстие.

а б в

Рис. 20.1

Рис. 20.2

Если закон преломления света всегда справедлив, то мы должны получить на экране светлый кружок. Действительно, если диаметр d отверстия не слишком мал по сравнению с расстоянием до экрана D, то так оно и есть (рис. 20.1, б). Но вот если d << D (например, d ~ 1 мм, D ~ 1 м), то картина на экране совершенно иная: в центре виден маленький светлый кружок, а вокруг него система концентрических колец (рис. 20.1, в). Причем если несколько уменьшить расстояние D при таком же d, то вместо светлого кружка в центре может оказаться темный кружок (рис. 20.2).

Согласитесь, «отклонение» от закона прямолинейного распространения света налицо!

Не менее удивительно ведут себя тени, отбрасываемые различными предметами на экран, если экран находится очень далеко от предмета. На рис. 20.3 показаны фотографии тени руки, держащей тарелку, при различных расстояниях от руки до экрана (рис. 20.3).

Рис. 20.3

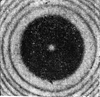Рис. 20.4

На рис. 20.4 показана фотография тени от непрозрачного круглого диска. Удивительно, что в самом центре этой тени находится светлое пятно!

Вспомним, что нечто похожее, а именно – огибание волнами препятствий, мы уже наблюдали, когда рассматривали механические волны на поверхности воды (рис. 20.5).

а б в

Рис. 20.5

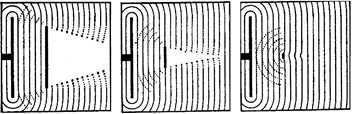
Когда препятствие достаточно велико по сравнению с длиной волны l (рис. 20.5, а), тень от него сравнительно резкая: лишь у самых краев тени заметно небольшое волнение, указывающее, что волна слегка огибает край препятствия. По мере уменьшения препятствия тень оказывается менее ясно выраженной (рис. 20.5, б), а когда размеры препятствия становятся сравнимыми с длиной волны, образования тени практически уже не происходит. На рис. 20.5, в видно, что в этом случае водяная волна огибает препятствие, и позади него она распространяется почти так же, как если бы препятствия не было.

Этот процесс огибания волнами препятствий называется дифракцией.

Принцип Гюйгенса

Читатель: А как теория объясняет дифракцию световых волн?

Автор: Одним из первых, кто попытался объяснить волновые свойства света, был нидерландский ученый Христиан Гюйгенс (1629–1695). В 1690 году он сформулировал утверждение, которое вошло в историю науки как принцип Гюйгенса.

Согласно принципу Гюйгенса каждую точку среды, которой достигла волна, можно рассматривать как источник вторичных сферических волн, распространяющихся со скоростью, свойственной среде.

Огибающая поверхность, т.е. поверхность, касающаяся всех сферических вторичных волн в том положении, которого они достигнут к моменту времени t, и представляет собой волновой фронт в данный момент.

На рис. 20.6 проиллюстрирован принцип Гюйгенса: показана поверхность волнового фронта Р₀ в момент времени t₀ = 0. Соответствующие вторичные волны изображены дугами, центры – кружочками, S – волновая поверхность в момент t, построенная как огибающая вторичных волн.

Рис. 20.6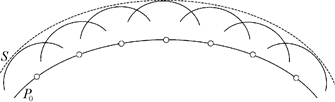

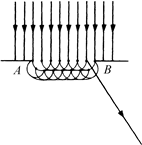Рис. 20.7

На рис. 20.7 показано, каким образом плоская волна, проходящая через щель АВ за счет вторичных волн начинает огибать края препятствия.

Читатель: А можно ли с помощью принципа Гюйгенса узнать, в какой точке будет достигаться минимум освещенности, а в какой максимум?

Автор: К сожалению, на этот вопрос принцип Гюйгенса ответа не дает.

Принцип Гюйгенса–Френеля

Принцип Гюйгенса был существенно уточнен французским физиком Огюстом Френелем (1788–1827). Основная идея Френеля состояла в том, что необходимо учитывать интерференцию вторичных волн.

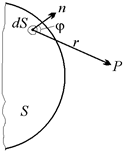Рис. 20.8

Пусть имеется некоторая волновая поверхность S, про которую мы знаем все, что нам надо: с какой амплитудой и в какой фазе колеблется каждый малый элемент dS этой поверхности. Нам необходимо выяснить, каким будет результирующее колебание в произвольной точке Р (рис. 20.8).

Согласно принципу Гюйгенса–Френеля каждый малый элемент dS волновой поверхности S служит источником вторичной волны, амплитуда которой пропорциональна величине элемента dS.

Амплитуда сферической волны убывает с расстоянием r от источника по закону 1/r. Следовательно, от каждого участка dS волновой поверхности в точку Р, лежащую перед этой поверхностью на расстоянии r от элемента dS, приходит колебание с амплитудой

,

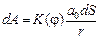где множитель а₀ определяется амплитудой колебания в том месте, где находится dS, а K(j) – коэффициент, зависящий от угла j между нормалью 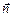к площади dS и направлением от dS к Р.

При j = 0 этот коэффициент максимален, при 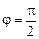он обращается в 0, при этом функция K(j) монотонно убывающая. (Точный вид функции K(j) для нас сейчас не важен.)

Разберемся теперь с фазой колебания.

Пусть все точки волновой поверхности колеблются в одинаковой фазе (wt + j₀). Тогда, если l – длина волны, колебание в точке Р будет отставать по фазе от колебания элемента dS на величину 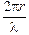. Следовательно, колебание в точку Р от элемента dS приходит с фазой .

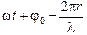Итак, в точку Р от элемента dS «приходит» колебание

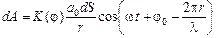. (20.1)

Результирующее колебание в точке Р представляет собой алгебраическую сумму (суперпозицию) колебаний, взятых по всей волновой поверхности S.

Зоны Френеля

Прямо скажем, проводить вычисления с помощью формулы (20.1) очень непросто. Поэтому, прежде чем мы приступим к теоретическому объяснению явлений дифракции света, нам понадобится ввести еще одно новое теоретическое понятие – зона Френеля.

Рассмотрим сферическую волну, распространяющуюся в однородной среде из источника S (рис. 20.9).

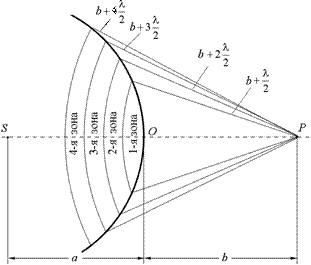
Рис. 20.9

Мысленно остановим волновой фронт, имеющий форму сферы радиуса а с центром в точке S на расстоянии b от точки наблюдения Р. Чтобы получить результирующее колебание, которое данная волновая поверхность создает в точке Р, нам надо разбить ее на маленькие участки dS_i и просуммировать колебания, создаваемые каждым таким участком согласно формуле (20.1).

Выполним «разбиение» следующим «хитрым» образом. Разделим сферическую поверхность на кольцевые зоны, как показано на рис. 20.9: граница каждой зоны представляет собой окружность, все точки которой равноудалены от точки Р на определенное расстояние. Для первой зоны это расстояние равно 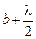для второй – 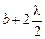, для третьей 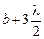, …, для п-й – .

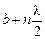Читатель: И в чем же «хитрость» такого разбиения?

Автор: А в том, что каждая четная зона будет «гасить» нечетную! В самом деле, давайте рассмотрим произвольный элемент dS₁, скажем, первой зоны, отстоящей от точки Р на расстоянии r (рис. 20.10).

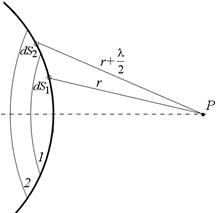Рис. 20.10

Для этого элемента мы всегда сможем найти во второй зоне парный ему элемент dS₂ такой же площади, отстоящий от точки Р на расстоянии 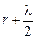. А это значит, что колебания от этих элементов придут в точку Р в противофазе, т.е. будут гасить друг друга. А поскольку обе зоны можно представить в виде совокупности таких пар, то четная зона погасит нечетную.

Читатель: Да, но при условии, что площади элементов dS₁ и dS₂ в паре будут равны или почти равны. Ведь если площадь одной зоны больше площади другой, полного гашения не получится.

Автор: В том-то и дело, что площади зон Френеля примерно равны, и мы это сейчас докажем.