Площадь зон Френеля

Заметим, что внешняя граница т-й зоны Френеля выделяет на волновой поверхности сферический сегмент высотой h_т (рис. 20.11).

Рис. 20.11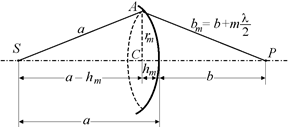

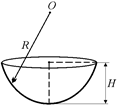Рис. 20.12

Из геометрии мы знаем, что площадь поверхности сферического сегмента радиусом R и высотой Н (рис. 20.12) равна

S = 2pRH. (20.2)

Рассмотрим прямоугольные треугольники SAC и РАС на рис. 20.11. По теореме Пифагора выразим катет r_т, который является общим для этих треугольников, через второй катет и гипотенузу:

для DSAC 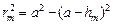, (1)

для DРАС 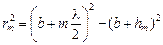. (2)

Приравняем правые части этих равенств и найдем h_m:

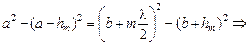
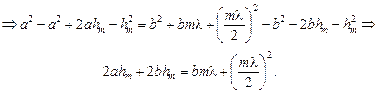
Учитывая, что длина световой волны l << а, l << b, членом 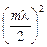можно пренебречь. Тогда

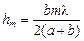. (20.3)

Теперь найдем площадь первых т зон:

.

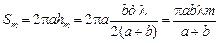Запомним:

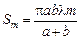. (20.4)

Найдем площадь т-й зоны как разность между площадью первых т зон и первых (т – 1) зон:

.

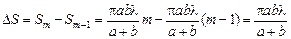Итак, мы получили важный результат: площадь зоны Френеля не зависит от ее порядкового номера, а значит, площади всех зон Френеля равны! Запомним:

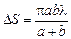. (20.5)

Теперь вычислим радиус т-й зоны. Воспользуемся формулой (1):

.

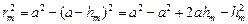При не слишком больших т h_m << a, а значит, числом 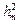можно пренебречь.

В самом деле, в выражении для h_m (формула (20.3)) в числителе стоит длина волны l, а l << а. Поэтому можно считать, что

.

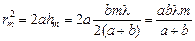Отсюда

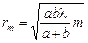. (20.6)

Оценим радиус 1-й зоны для случая а = 1 м, b = 1 м и l = 500 нм, получим

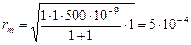м = 0,5 мм.