Дифракция световых волн: принцип Гюйгенса-Френеля 4 страница

1 - ой зоныФренеля с r₁ радиусом. Поэтому в (10.91) слагаемым А_m/2 можно пренебречь по сравнению с А₁/2, что является признаком отсутствия дифракцииФренеля. На Э экране в этом случае получается равномерноосвещённое изображение щели, которое строится по законам геометрической оптики.

При: m >> 1 ↔ d/(λb)^{1/ 2} >> 1 ↔ d >> (λb)^1/2 (10.146) на Э экране получается равномерноосвещённое изображение щели, которое строится по законам геометрической оптики. Из (10.144), (10.145) и (10.146) критериемприменимости либо законов геометрической оптики, либо дифракцииФренеля, либо дифракцииФраунгофераявляется не малость λдлинысветовой волны в однородной изотропной среде с n показателем преломления по сравнению с характерным размером преграды, например, (рис. 10.36) d ширинойщели, а значение (10.143)

m параметра, т.е. количества зонФренеля, открываемых этой преградойна Э экране.

Формирование дифракционной картины при нормальном падении плоской монохроматической проходящей световой волны на дифракционную решётку.

Формирование дифракционной картины при наклонном падении плоской монохроматической проходящей световой волны на дифракционную решётку. Формирование дифракционной картины при наклонном падении плоской монохроматической световой волны на отражательную дифракционную решётку. Спектральные характеристики дифракционных решеток: угловая и линейная дисперсия. Угловая ширина главного дифракционного максимума нулевого порядка плоской монохроматической световой волны. Разрешающая способность дифракционной решёткипо критерию Релея. Дифракция рентгеновских лучей на линейных цепочках структурных элементов. Формулы Лауэ. Понятие о рентгеноструктурном анализе.

Формирование дифракционной картины при нормальном падении на дифракционную решётку плоской монохроматической проходящей световой волны

Для осуществления многолучевой интерференциисветовых волн с близкими или равными

A амплитудами Aсветовых векторов применяют специальные интерференционныеприборы, например, дифракционную решётку.

После прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломления нормально поверхности ДРдифракционной решётки, имеющей форму (рис.10.34) щелей бесконечной длины по перпендикулярнойплоскости чертежа OX оси, dширинойпо OY оси и h расстоянием между щелями, I_υ интенсивность световойволныв произвольный момент t времени в M точке на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, определяется из (10.138) выражения дифракцииФраунгоферанащелиdшириной.

Дифракционная решёткаДР имеет N щелей, поэтому вторичнаясферическая волна, распространяющаяся параллельным пучком от каждой из этих N щелей под υ углом к главной оптическойOZ осиЛ линзы фокусируется этой Л линзойв её фокальнойплоскости в M точке на

Э экране.

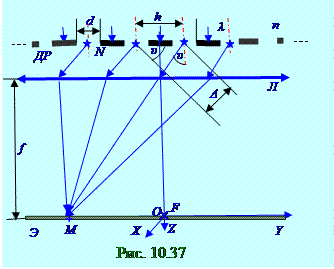
следующий вид: δ = 2πΔ/λ = (2π/λ)hsinυ. (10.148) где λ - длинасветовой волны в изотропной среде с n показателем преломления, поэтому оптическаяλ = λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.37Векторы A_υ амплитудысветовых векторов от соседних световых волн имеют равные

A_υ модули, т.к. их оптические путираспространенияот каждой из N щелейдоM точки на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, одинаковы.Разность(10.148) Ф_υk+1 - Ф_υk = δ фазмеждувекторами A_υ амплитудсветовых векторов от k+1-ой исоседнейk-ой щелями

ДРдифракционной(рис. 10.37) решёткиу световыхлучей, распространяющихся параллельным пучком от каждой из N щелейпод υ углом к главной оптическойOY осиЛ линзы, одинаковаи равна следующей постоянной величине: Ф_υk+1 - Ф_υk = δ = const.(10.149)

Согласно представлению гармоническихколебаний на векторной диаграмме (рис.2.3)из раздела 2.0 "Колебания и волны"результирующий вектор A_υр световых векторов от всехN щелейбудет равен сумме векторов A_υ амплитуды светового вектораот каждой из N щелейдо M точки на Э экране, т.е. под υ углом к главной оптической осиЛ линзы.

Если количество (рис. 10.37) щелей N₁, то результирующий вектор A_υN1 амплитуды световых векторов от всехN₁ щелейбудет равен сумме векторов A_υ амплитуды светового вектораот каждой из N₁ щелейдоM точки на Э экране, т.е. под υ углом к главной оптической осиЛ линзы.

Графически (рис. 10.38) этот результирующий вектор A_υN1 определится суммой, например, 3 - х векторов A_υ, направленных под δ углом друг к другу и являющихся основаниямиравнобедренных треугольников с δ углами между равными OO₁ сторонами.

В равнобедренном треугольнике с основанием, равным модулю A_υвектора A_υ амплитуды светового вектораот (рис. 10.37) каждой из N₁ щелей, и δ углом при вершинеэтого равнобедренного треугольника, равным (рис. 10.38) разности(10.148)δ фазмеждувекторами A_υ амплитуд светового вектора от соседних щелейДРдифракционнойрешётки, длина OO₁ стороны имеет следующий вид: OO₁ =(A_υ/2)/|sin(δ/2)|.(10.150) МодульA_υN1 результирующего вектора A_υN1 амплитуды световых векторов от всех

N₁ щелей определится из равнобедренного треугольника, основанием которого является этот результирующий вектор A_υN1, а α₁ уголпри вершине этого равнобедренного треугольника имеет следующий вид: α₁ = N₁δ. (10.151)

Для случая (рис. 10.38) N₁ = 3, т.е. 3 - х щелей у ДРдифракционнойрешётки, A_υN1 модуль

A_υN1 результирующего вектора с учётом (10.151) имеет следующий вид:

максимальным, что означает существованиедифракционного максимума на Э экране под этим υ углом к главной оптической осиЛ линзыи этого числа N₂ щелейу ДРдифракционнойрешётки. При увеличении числа Nщелей (рис. 10.38) до величины N₃, например, до 6 -ти модульA_υN3 результирующего вектора A_υN3амплитуды световых векторов от всехN₃ щелейв M точке

(рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, с учётом (10.152) принимает следующий вид:

A_υN3 = 2OO₁| sin(α₂/2)| = 2OO₁|sin[π - (N₃δ/2)]| = 2OO₁|sin(N₃δ/2)| = A_υ|[sin(N₃δ/2)]/[sin(δ/2)]|.(10.154) По сравнению с A_υmaxмодулемпри числе N₂ щелей, например (рис. 10.38), равным 4 -ём,модульA_υN3 результирующего вектора A_υN3амплитуды световых векторов от всехN₃ щелейв

M точке (рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, стал меньше.

При числе Nщелей, например (рис. 10.38), равным 8 - ми,модульA_υmin результирующего вектора A_2minамплитуды световых векторов от всехN щелейв M точке (рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, становится равным нулю, что означает существование дифракционного минимума на Э экране под этим υ углом к главной оптической осиЛ линзыи этого числа Nщелейу ДРдифракционнойрешётки.

Из сравнения (10.155) и (10.156) при произвольном значении числа NщелейA_υN модуль результирующего вектора A_υN амплитуды световых векторов от всехN щелейв M точке

(рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, имеет следующий вид: A_υN = A_υ|[sin(Nδ/2)]/[sin(δ/2)]|.(10.155) По аналогии с (10.138) I_υNинтенсивность световойволны после прохожденияпараллельнымпучком ДРдифракционной решёткис Nщелямипропорциональнаквадрату A_υN ²амплитуды результирующего вектора A_υN амплитуды световых векторов в M точке (рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, и эта I_υNинтенсивность световойволны с учётом (10.155) имеет следующий вид: I_υN = I_υ [sin²(Nδ/2)]/ [sin²(δ/2)], (10.156) где I_υ - интенсивность световойволны от одной щели (рис. 10.35) в M точке (рис. 10.37) на Э экране, т.е. под υ углом к главной оптической осиЛ линзы.

Подставляем (10.138) интенсивность световойволны от одной щели (рис. 10.32) в M точке на Э экране, т.е. под υ углом к главной оптической осиЛ линзы, в (10.156) и получаем следующее выражениеI_υNинтенсивности световойволны после прохожденияпараллельнымпучком ДРдифракционной решёткис Nщелями:

I_υN = I_dsin²[(πdsinυ)/λ]/[(πdsinυ)/λ]²[sin²(Nδ/2)]/ [sin²(δ/2)], (10.157) где I_d - интенсивность(рис. 10.37)световойволны после прохожденияпараллельнымпучком одной щели dширинойв центреЭ экрана. Подставляем (10.148) разностьδ фазмеждусоседними световыми лучамис λ длиной волны в (10.157) и получаем следующее выражение I_υNинтенсивности световойволны после прохожденияпараллельнымпучком дифракционной ДР решёткис Nщелямиdшириной, расстояние между которыми равно h, под (рис. 10.37) υ углом к главной оптической осиЛ линзы: I_υN = I_d[ sin²(πdsinυ/λ)]/(πdsinυ/λ)²] [sin²(Nπhsinυ/λ)]/[sin²(πhsinυ/λ)]. (10.158) Второй сомножитель в (10.158) имеет следующий предел: lim[sin²(Nπhsinυ/λ)/sin²(πhsinυ/λ)] = N². (10.159) |hsinυ| → mλ, где m = 0, 1, 2, … Согласно (10.158) интенсивностьI_υmaxN световойволны после прохожденияпараллельнымпучком ДРдифракционной решёткис Nщелямиdшириной, расстояние между которыми равно h, под (рис. 10.37) υ_max углом к главной оптической осиЛ линзыимеет следующий вид: I_υmaxN = I_d[ sin²(πdsinυ_max /λ)]/(πdsinυ_max /λ)²] N²_, (10.160) если υ_max угол к главной оптической осиЛ линзы, под которым производят наблюдение дифракционной картины(рис. 10.37) на Э экране удовлетворяет следующему условию:

hsinυ_imax = ± mλ, (10.161) где υ_imax - i - ое значение угла (рис. 10.37) к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимумаm - ого порядка.

На Э экране (рис. 10.37) после прохожденияпараллельнымпучком ДРдифракционной решёткис Nщелямиdшириной, расстояние между которыми равно h, под υ_max углом (10.161) к главной оптической осиЛ линзы колебания Aсветовых векторов световой волны от отдельных щелейвзаимно усиливаютдруг друга. Поэтому m число в условии (10.161) определяет порядок главных дифракционных максимумов.

При (10.161) m = 0 и следовательно при υ_0max = 0 наблюдают (рис. 10.37) дифракционный максимум нулевого порядка на Э экране в 0 начале координат. Дифракционных максимумов

1-го, 2-го, 3-го и т.д. порядков имеется по два при (10.161) соответственно m = 1 и m = -1, m = 2

и m = -2, m = 3 и m = -3 и т.д.

Согласно (10.161)длядифракционных максимумов1-го, 2-го и т.д. порядков, которые наблюдаются на Э экране под υ_imax углами к главной оптической осиЛ линзы справедливо следующее соотношение: |sinυ_imax| = mλ/h.(10.162) По свойствам тригонометрическойфункции справедливо следующее соотношение:

|sinυ_imax| ≤ 1. (10.163) Подставляем (10.162) в (10.163) и получаем следующиезначения m_в порядков главных дифракционных максимумов, которые возможно наблюдать вдифракционной картине:

m_вλ/h ≤ 1 ↔ m_в ≤ h/λ. (10.164)

Формирование дифракционной картины при наклонном падении на дифракционную решётку плоской монохроматической проходящей световой волны

После прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломления(рис. 10.39) под +θуглом падениянаповерхность

ДРдифракционной решётки, имеющей форму щелей бесконечной длины по перпендикулярнойплоскости чертежа OX оси, dширинойпо OY оси и h расстоянием между щелями, оптическая Δ_+υ-m разность хода двух параллельныхлучей,отстоящихдруг от другана h расстоянии и имеющих

+υ_-m угол между направлением лучей и нормальюк поверхностиДРдифракционной решёткиимеет с учётом (10.147) следующий вид: Δ_+υ-m = hsin+υ_-m, (10.165)

где знак "+" плюс означает, что υ_-m угол отсчитывается от нормалик поверхности

ДРдифракционной решёткипо"часовой стрелке".

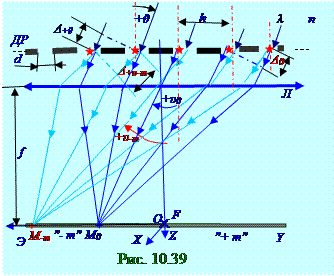
Оптическая Δ_+θ разность хода двух параллельныхлучей,падающих (рис. 10.39) под

+θ угломотносительнонормалик поверхностиДРдифракционной решётки, отстоящимидруг от другана h расстоянии, имеет с учётом (10.147) следующий вид: Δ_+θ = hsin(+θ). (10.166) Общая оптическая Δ_o+θ разность хода двух параллельныхлучей, падающих (рис. 10.39) под

+θ угломотносительнонормалик поверхностиДРдифракционной решётки, и выходящих из

N щелей в виде вторичнойсферическая волна под +υ_-m углом, имеет с учётом (10.165), (10.166) следующий вид: Δ_o+θ = Δ_+θ - Δ_+υ-m = hsin(+θ) - hsin(+υ_-m), (10.167) где знак "-" минус присутствует, потому что верхний из падающих (рис. 10.39) под

+θ угломотносительнонормалик поверхностиДРдифракционной решётки световых лучей на величину Δ_+θ имеет бόльшую оптическую длину по сравнению с нижнимсветовым лучом, а верхний извыходящих из N щелей в виде вторичнойсферической волны под +υ_-m углом световых лучей на величину Δ_+υ-m имеет меньшую оптическую длину по сравнению с нижнимсветовым лучом.

Условие наблюдение главного дифракционного максимумаm - ого порядка (рис. 10.39) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод +θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.167) следующий вид: Δ_o+θ = hsin(+θ) - hsinυ_imax= ± mλ, (10.168)

где υ_imax - i - ое значение угла к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимумаm - ого порядка.

Условие наблюдение главного дифракционного максимума0 - ого порядка (рис. 10.39) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод +θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.168) следующий вид: Δ_o+θ = hsin(+θ) - hsin(+υ₀) = 0 ↔ +θ =+υ₀, (10.169)

где+υ₀ - значение угла к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимума0 - ого порядка, которое равно +θуглу падениянаповерхностьДРдифракционной решётки параллельногопучка световой волныв однородной изотропной среде с n показателем преломления.

Условие наблюдение главного дифракционного максимума"- m" порядка (рис. 10.39) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод +θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.168) следующий вид:

Δ_o+θ = hsin+θ - hsin(+υ_-m)= - mλ ↔ sin(+υ_-m) =(mλ/h) + sin(+θ), (10.170)

где+υ_-m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума"- m" порядка, наблюдаемого на Э экране в положительной области

OY оси; m - модуль порядка главного дифракционного максимума.

Условие наблюдение главного дифракционного максимума"+ m" порядка (рис. 10.39) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод +θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.168) следующий вид:

Δ_o+θ = hsin+θ - hsin(υ_+m)= mλ ↔ sin(υ_+m) = sin(+θ) - (mλ/h), (10.171)

где υ_+m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", если в (10.173) sin(+θ) > mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в отрицательной области OY оси; υ_+m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", если в (10.171) sin(+θ) < mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в отрицательной области

OY оси; m - модуль порядка главного дифракционного максимума.

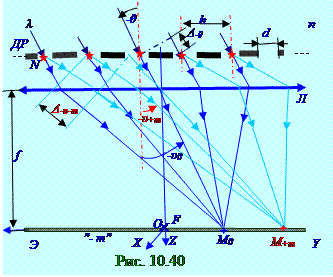
Условие наблюдение главного дифракционного максимумаm - ого порядка (рис. 10..40) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод -θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.168) следующий вид: Δ_o-θ = hsin(-θ) - hsinυ_imax= ± mλ, (10.172)

где υ_imax - i - ое значение угла к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимумаm - ого порядка.

Условие наблюдение главного дифракционного максимума0 - ого порядка (рис. 10.40) на Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод -θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.172) следующий вид: Δ_o-θ = hsin(-θ) - hsin(-υ₀) = 0 ↔ -θ =-υ₀, (10.173)

где -υ₀ <0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума0 - ого порядка, которое равно -θ углу падениянаповерхностьДРдифракционной решётки параллельногопучка световой волныв однородной изотропной среде с n показателем преломления.

Условие наблюдение главного дифракционного максимума"+ m" порядка (рис. 10.40) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод -θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.172) следующий вид:

Δ_o-θ = hsin(-θ) - hsin(-υ_+m)= mλ ↔ sin(-υ_+m) = sin(-θ) - (mλ/h), (10.174)

где -υ_+m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума"+ m" порядка, наблюдаемого на Э экране в отрицательной области

OY оси; m - модуль порядка главного дифракционного максимума.

Условие наблюдение главного дифракционного максимума"- m" порядка (рис. 10.40) на

Э экране от прохожденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломленияпод -θуглом падениянаповерхностьДРдифракционной решётки, имеет с учётом (10.172) следующий вид:

Δ_o-θ = hsin(-θ) - hsin(υ_-m)= -mλ ↔ sin(υ_-m) = sin(-θ) + (mλ/h), (10.175)

где υ_-m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив "часовой стрелке", если с учётом sin(-θ) < 0 в (10.175) |sin(-θ)| > mλ/h и тогда наблюдение главного дифракционного максимума"- m" порядка наблюдается на Э экране в положительной области OY оси; υ_-m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", если с учётом sin(-θ) < 0 в (10.175) |sin(-θ)| < mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в положительной области OY оси; m - модуль порядка главного дифракционного максимума.