Дифракция световых волн: принцип Гюйгенса-Френеля 2 страница

Согласно (рис. 10.23) результирующий (рис. 10.3) из раздела 10.1 "Электромагнитная природа света. Интерференция света" вектор амплитудыA светового вектора сферической световой волны в M точке пространства от двух зон Френеля с r₂ радиусом, построенный с помощью спирали Френеля, имеет A амплитуду, примерно равную нулю, что согласуется с выражением (10.90)

А ≈ А₁/2 - А₂/2 при двух открытыхзонахФренеля, которое также примерно равно нулю, вследствие того, что А₁ амплитуда первой зоны Френеля примерно равна

А₂ амплитуде от соседнейвторой зоны Френеля.

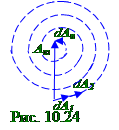
амплитуды (рис. 10.16) открытой только первой зоныФренеля, что согласуется с выражением (10.84) А = А₁ - А₂ + А₃ - А₄ + … ≈ А₁/2, выведенное для Арезультирующей амплитуды

A светового вектора сферической световой волны в M точке пространствана Э экране от открытыхm - зонФренеля.

Графический метод расчёта дифракции световых волн от круглого диска с помощью спирали Френеля

Применение графического метода расчёта, т.е. с помощью спирали Френеля,

A_ост результирующего (рис. 10.3) вектора амплитудыA светового вектора сферической световой волны в M точке пространства на Э экране, когданепрозрачныйД диск закрывает m первых

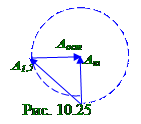
Вектор (рис. 10.18) A _ост амплитудыA светового вектора сферической световой волны в

M точке пространства на Э экране, когданепрозрачный Д диск закрывает, например, полторы первых зонФренеляс помощью спирали Френеляопределится(рис. 10.23) сложением

A_1,5 результирующего вектора амплитудысветовой волны от закрытыхполторы первых зонФренеля с A _ост результирующим вектором амплитудысветовой волны от всех оставшихся незакрытыхзонФренеля, вследствие чего имеет место следующее выражение:

A_∞ = A_1,5 + A _ост ↔A _ост = A_∞ -A_1,5, (10.108)

где (рис. 10.25) A_∞ - результирующий вектор амплитудыA светового вектора сферической световой волны в M точке пространства на Э экране (рис. 10.16) от всех зон Френеля, если бы они все были открыты, т.е. не существовало бы непрозрачного Д диска закрывающего, например, полторы первых зонФренеля.

Применение метода зон Френеля в дифракции световых волн от зонной пластинки

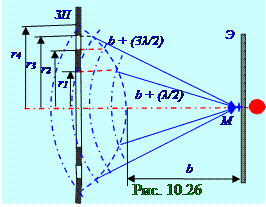
В M точку пространства на Э экране (рис. 10.26) приходятсветовые волны от нечётных зон Френеля с r₁, r₃ радиусами, поскольку чётные зоны Френеля с r₂, r₄ радиусамиперекрыты непрозрачнойЗП зонной пластинкой.

Результирующий (рис. 10.3) вектор A амплитудыA светового вектора сферической световой волны в M точке пространства на Э экране от только нечётных зон Френеля с

r₁, r₃ радиусами имеет, (10.84) вследствие отсутствия A₂, A₄ противофазных составляющих от чётных зон Френеля с r₂, r₄ радиусами, A амплитуду следующего вида:A = A₁ + A₃ ≈ 2A₁ = 4(А₁/2), (10.109)

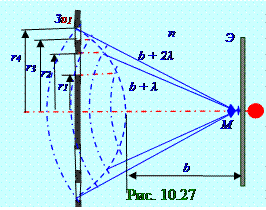
где амплитуда А₁ первой зоны Френеля примерно равнаамплитуде А₃ от соседнейтретьейзоны Френеля. В M точку пространства на Э экране (рис. 10.27) приходятсветовые волны от чётных зон Френеля с r₂, r₄ радиусами, поскольку нечётные зоны Френеля с r₁, r₃ радиусамиперекрыты непрозрачнойЗП зонной пластинкой.

Результирующий (рис. 10.3) вектор A амплитудыA светового вектора сферической световой волны в M точке пространства на Э экране от только чётных зон Френеля с r₂, r₄ радиусами имеет, (10.84) вследствие отсутствия A₁, A₃ противофазных составляющих от нечётных зон Френеля с r₁, r₃ радиусами, A амплитуду следующего вида:A = A₂ + A₄ ≈ 2A₂= 4(А₂/2), (10.110)

где А₂ амплитуда второй зоны Френеля примерно равнаА₄ амплитуде от соседнейчетвёртойзоны Френеля. Согласно (10.109), (10.110) применение ЗП зонной пластинки позволяет увеличить

А амплитуду результирующего A светового вектора сферической световой волны в M точке пространства на Э экране по сравнению с одной открытойзоной Френеля более, чем в 2 раза.

в M точке пространства на Э экране по сравнению с одной открытойзоной Френеля при применении ЗП зонной пластинки с n перекрытыми чётными или нечётными зонами Френеля, увеличивается приблизительно в n² раз, т.е. имеет место следующее приблизительное соотношение: I ≈ n²I₁,(10.111) где I₁ - интенсивность световойволны в M точке пространства на Э экране с одной открытойзоной Френеля; n - количество перекрытых зон Френеляв ЗП зонной пластинкой, которое для случая на

рис. 10.26, рис. 10.27 равно двум.

Применение метода зон Френеля в дифракции световых волн от пластинки Вуда

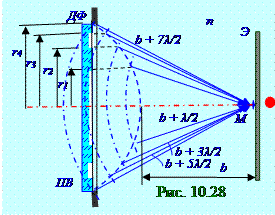
с r₁, r₂, r₃ , r₄ радиусами имеет (10.84) вследствие отсутствия противофазных составляющих A амплитуду, имеющую следующий вид: А = А₁ + А₂ + А₃ + А₄ ≈ 4A₁, (10.112)

где А₁ амплитуда первой зоны Френеля примерно равнаА₂, А₃, А₄ амплитудамот соседнихвторой, третьейичетвёртой зон Френеля.

Интенсивность(рис. 10.8) I_Всветовойволны в M точке пространства на Э экране при использовании ПВ пластинки Вуда с n чётными или нечётными зонами Френелясвязана приблизительным следующим соотношением: I_В ≈ 4n²I₁,(10.113)

где I₁ - интенсивность световойволны в M точке пространства на Э экране с одной открытойзоной Френеля; n - количество чётных или нечётных зон Френеляв ПВ пластинке Вуда, который для случая на рис.10.28 равно двум.

Графический метод расчёта дифракции Френеля световых волн от полуплоскости с помощью спирали Корню

Монохроматическая плоская световая волна в однородной изотропной среде с

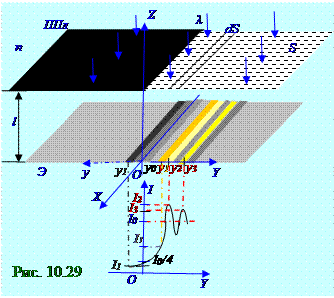
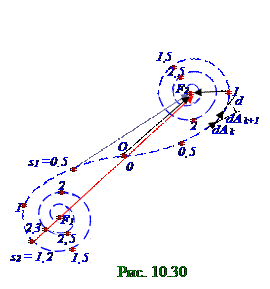
n показателем преломления, поэтому оптическаяλ= λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.29, падает нормальнона непрозрачную ППл полуплоскость. Правее непрозрачной ППл полуплоскости плоскийволновой фронт световой волны S площадью разбит на узкие одинаковой ширины прямолинейные dS площадки, параллельные краю ППл полуплоскости.

Результирующий вектор A амплитудысветового вектора A монохроматической плоской световой волны на Э экране будет одинаков по OX оси, но зависит от y координаты, т.к. по аналогии (рис. 10.21) c узкимикольцевыми зонами Френеля будет равен сумме элементарных векторов

dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадью плоскоговолнового фронта световой волны S площадью. Разность Ф _k+1 - Ф_k = dφ фаз у световых волн, пришедших на Э экран на линию с y координатой от соседних узкихпрямолинейных элементарных поверхностей dS площадью волнового фронта световой волны S площадью соответственно с элементарными векторами dA _k+1, dA _k, постоянен, а модули (рис. 10.29) dA₁, dA₂, …, dA_n элементарных векторов dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадьюволнового фронта световой волны S площадью, пришедших на Э экран на линию с

y координатой,убывают по поверхности dS площадьюот этой линии с y координатой. По этой причине фигура (рис. 10.30), составленная из соседних векторов dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадью представляет собой закручивающуюсяспираль, называемую спиралью Корню, с постепенным уменьшением радиуса этой спирали по мере увеличения расстояния узкойпрямолинейной элементарной поверхности dS площадью на плоскомволновом фронтесветовой волныдо линии на Э экране с y координатой.

Для линии на Э экране геометрической тени непрозрачной ППл полуплоскости, т.е. с y₀ = 0 координатой и находящейся на OX оси, результирующий вектор A амплитудысветового вектора

A монохроматической плоской световой волны на Э экране будет равен сумме элементарных векторов dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадью, находящихся правее OX оси и количество которых неограниченно. Амплитуда A вектора A плоской световой волны линии на Э экране с y₀ = 0 координатой определится по аналогии (рис. 10.21) срезультирующим вектором A_∞ амплитудысветового вектора A монохроматической плоской световой волны длиной 0F₂ вектора из (рис. 10.30) O центра спирали Корню, который обозначен s параметром этой спирали Корню, равным нулю, т.е. s = 0, в правыйF₂ фокус спирали Корню.

Для линии (рис. 10.29) на Э экране с y₁ координатой и находящейся правее OX оси результирующий вектор A₁амплитудысветового вектора A₁монохроматической плоской световой волны на Э экране будет равен сумме элементарных векторов dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадью, находящихся правеепоOY оси

y₁ координаты и количество которых неограниченно, а также будет равен сумме элементарных векторов dA₁, dA₂, …, dA_n от каждой узкойпрямолинейной элементарной поверхности dS площадью, находящихся левее поOY оси y₁ координаты и количество которых ограниченно.

Амплитуда A₁ вектора A₁ плоской световой волны линии на Э экране с y₁ координатой и находящейся правее OY оси, определится длиной вектора (рис. 10.1.30), направленного из левой части спирали Корнюс s₁ параметром в правыйF₂ фокус спирали Корню.

Параметр (рис. 10.30) s спирали Корнюзависит (рис. 10.29) от l расстояния Э экрана до непрозрачной ППл полуплоскости, длины λнормальнопадающей на непрозрачную ППл полуплоскостьсветовой волны и y расстояния линии на Э экране, параллельной OX оси, в которой определяется амплитуда A вектора A плоской световой волны, и определяется по следующему соотношению: s = y(2/lλ)^1/2. (10.114)

Параметр (рис. 10.30) s₁ спирали Корню дляопределения амплитуды A₁ вектора A₁ плоской световой волны линии на Э экране с y₁ координатой и находящейся правее OX оси, определится из значения этой y₁ координаты с использованием (11.102) выражения: s₁ = y₁ (2/lλ)^1/2. (10.115)

Для примера y₁ координата линии на Э экране принята такой величины, что (рис. 10.1.0.28) параметр s₁ на спирали Корнюравен 0, 5, т.е. s₁ = 0, 5.

Первыйдифракционный максимум (рис. 10.29) с I₂ интенсивностью (10.17)световой волны образуется на Э экране на линии с y₂ координатой, параллельной OX оси, которой соответствует параметр (рис. 10.30) s спирали Корню, равный 1_,2, т.е. y₂ координата, на которой существует первый дифракционный максимум, определяется с использованием (10.116) выражения и имеет следующий вид: y₂ = 1, 2/(2/lλ)^1/2 . (10.116)

Амплитуда A₂ вектора A₂ плоской световой волны первого дифракционного максимума, находящегося на Э экране на линии с y₂ координатой, определится длиной вектора (рис. 10.30), направленного из левой части спирали Корнюс s₂ параметром, равным 1_,2, в правыйF₂ фокус спирали Корню.

Вектор (рис. 10.30), направленный из левой части спирали Корнюс s₂ параметром,

равным 1_, 2, в правыйF₂ фокус спирали Корнюявляетсясуммой двух векторов, а именно: вектора, направленного из левой части спирали Корнюс s₂ параметром, равным 1_, 2, в O центр спирали Корню, и вектора, направленного из O центра спирали Корню в правыйF₂ фокус.

Длина вектора (рис. 10.30), направленного из левой части спирали Корнюс s₂ параметром, равным 1_, 2, в O центр спирали Корню, определяет A_2лев амплитуду вектора A_2лев плоской световой волны при образовании первого дифракционного максимума, находящегося на Э экране на линии с y₂ координатой, от каждой узкойпрямолинейной элементарной поверхности dS площадью на плоскомволновом фронтесветовой волны S площадью, находящихся левее y₂ координаты и количество которых ограниченно.

Длина вектора (рис. 10.30), направленного из O центра спирали Корню в правыйF₂ фокус этой спирали Корню, определяет A_2пр амплитуду вектора A_2пр плоской световой волны при образовании первого дифракционного максимума, находящегося на Э экране на линии с y₂ координатой, от каждой узкойпрямолинейной элементарной поверхности dS площадью на плоскомволновом фронтесветовой волны S площадью, находящихся правее y₂ координаты и количество которых неограниченно.

Второйдифракционный максимум (рис. 10.29) с I₃ интенсивностью (10.17)световой волны образуется на Э экране на линии с y₃ координатой, параллельной OX оси, которой соответствует параметр (рис. 10.30) s спирали Корню, равный 2_, 3, т.е. y₃ координата, определяется с использованием (10.116) выражения и имеет следующий вид: y₃ = 2_, 3/(2/lλ)^1/2. (10.117)

Амплитуда A₃ вектора A₃ плоской световой волны при образовании второго дифракционного максимума, находящегося на Э экране на линии с y₃ координатой, определится длиной вектора

(рис. 10.30), направленного из левой части спирали Корнюс s₃ параметром, равным 2_, 3, вправыйF₂ фокус спирали Корню.

Амплитуду A₀ вектора A₀ плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости определяют по измерению длины вектора (рис. 10.30), направленного из левого F₁ фокуса спирали Корню в правыйF₂ фокус этой спирали Корню.

Далее определяют отношение длины вектора (рис. 10.30), например, определяющего

A₃ амплитуду вектора A₃ плоской световой волны при образовании второго дифракционного максимума, находящегося (рис.10.29) на Э экране на линии с y₃ координатой, к длине вектора, определяющего A₀ амплитуду вектора A₀ плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости, которое, например, имеет следующее значение: A₃/A₀ = η. (10.118)

Поскольку Iинтенсивность(10.17) световойволны пропорциональна квадратуA амплитуды вектора A плоской световой волны, т.е. I ~ A², то выражение, например, для отношения I₃ интенсивности плоской световой волны при образовании второго дифракционного максимума, находящегося (рис. 10.29) на Э экране на линии с y₃ координатой, к I₀ интенсивности этой же плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости с учётом (10.118) имеет следующий вид: I₃= kA₃² ↔ I₃/I₀ = A₃²/A₀² ↔ I₃/I₀ = η², (10.119) I₀ = kA₀²

где k – коэффициент пропорциональности между Iинтенсивностью и A амплитудой вектора A световой волны.

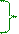Для линии на Э экране геометрической тени непрозрачной ППл полуплоскости, т.е. с y₀ = 0 координатой и находящейся на OX оси, амплитуда A вектора A плоской световой волны определится длиной 0F₂ вектора из (рис. 10.30) O центра спирали Корню, который обозначен s параметром этой спирали Корню, равным нулю, т.е. s = 0, в правыйF₂ фокус спирали Корню. Амплитуда A₀ вектора A₀ плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости определяют по измерению длины вектора (рис. 10.30), направленного из левого F₁ фокуса спирали Корню в правыйF₂ фокус этой спирали Корню, вследствие чего имеет место следующее соотношение: A/A₀ = 1/2. (10.120) Отношение(рис. 10.29) I интенсивности плоской световой волны для линии на Э экране геометрической тени непрозрачной ППл полуплоскости, т.е. с y₀ = 0 координатой, к I₀ интенсивности этой же плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости с учётом (10.120) имеет следующий вид: I= kA² ↔ I/I₀ = A²/A₀² ↔ I/I₀ = 1/4, (10.121) I₀ = kA₀²

где k – коэффициент пропорциональности между Iинтенсивностью и A амплитудой вектора A световой волны.

Амплитуда A₁ вектора A₁ плоской световой волны линии на Э экране (рис. 10.29)

y₁ координатой и находящейся левее OX оси, определится длиной вектора (рис. 10.30), направленного из правой части спирали Корнюс s₁ параметром в правыйF₂ фокус спирали Корню.

Параметр s₁ спирали Корнюдляопределения амплитуды A₁ вектора A₁ плоской световой волны линии на Э экране с y₁ координатой, находящейся (рис. 10.29) левее OX оси, определится из значения этой y₁ координаты с использованием (10.116) выражения, вследствие чего для параметра

(рис. 10.30) s₁ спирали Корню имеет место следующее соотношение: s₁ = y₁(2/lλ)^1/2. (10.122)

Для примера y₁ координата линии на Э экране принята такой величины, что (рис. 10.30) параметр s₁ на спирали Корнюравен 1, т.е. s₁ = 1.

Амплитуда A₁ вектора A₁ плоской световой волны на Э экране на линии с y₁ координатой, находящейся (рис. 10.29) левее OX оси, определится длиной вектора (рис. 10.30), направленного из правой части спирали Корнюс s₁ параметром, равным 1, в правыйF₂ фокус спирали Корню.

Отношение длины вектора (рис. 10.30), определяющего A₁ амплитуду вектора A₁ плоской световой волны на Э экране на линии y₁ координатой, находящейся (рис. 10.29) левее OX оси, к длине вектора, определяющего A₀ амплитуду вектора A₀ плоской световой волны на Э экране при отсутствии непрозрачной ППл полуплоскости, например, имеет следующее значение: A₁/A₀ = ξ.(10.123)

Отношение I₁ интенсивности плоской световой волны на Э экране на линии с y₁ координатой, находящейся (рис. 10.29) левее OX оси, к I₀ интенсивности этой же плоской световой волны на

Э экране при отсутствии непрозрачной ППл полуплоскости с учётом (10.120) имеет следующий вид:

I₁= kA₁² ↔ I₁/I₀ = A₁²/A₀² ↔ I₁/I₀ = ξ², (10.124) I₀ = kA₀²

где k – коэффициент пропорциональности между Iинтенсивностью и A амплитудой вектора A световой волны.

Таким образом, при дифракции Френеля (рис. 10.29) справа на Э экране от геометрической тени непрозрачной ППл полуплоскостиобразуютсядифракционные максимумы и минимумыс уменьшающейсяконтрастностьюпо мере удаления вправо от этой геометрической тени непрозрачной ППл полуплоскости.