Дифракция световых волн: принцип Гюйгенса-Френеля 3 страница

Слева(рис. 10.29) на Э экране от геометрической тени непрозрачной ППл полуплоскостипри дифракции Френеля резкого перехода от освещённой области к неосвещённой не будет, а будет монотонное уменьшение освещённости по мере удаления влево от этой геометрической тени непрозрачной ППл полуплоскости.

Дифракцию Френеля (рис. 10.29) от полуплоскости можно наблюдать при линейных размерах l расстояния Э экрана до непрозрачной ППл полуплоскости, длины λнормальнопадающей на непрозрачную ППл полуплоскостьсветовой волны и y расстояния линии на Э экране, при которых параметр s спирали Корнюнаходится в областизначений, указанных на рис. 10.30.

Графический метод расчёта дифракции Френеля световых волн от щели в плоскости с помощью спирали Корню

Монохроматическая плоская световая волна в однородной изотропной среде с

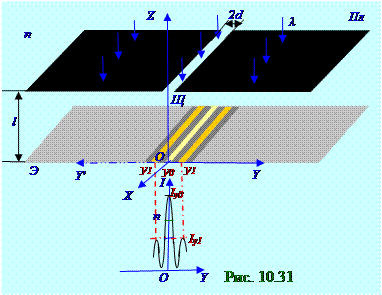
n показателем преломления, поэтому оптическаяλ= λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.31, падает нормальнона бесконечную непрозрачную

Пл плоскость, в которой по OX оси существует бесконечная Щ щель с 2d шириной.

Амплитуда A_1пр вектора A_1пр плоской световой волны линии на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскости с y₀координатой от (рис. 10.31) каждой узкойпрямолинейной элементарной поверхности dS площадью на плоскомволновом фронтесветовой волны S площадью, находящихся правее y₀ координаты и количество которых ограничено, определится длиной вектора (рис. 10.32), направленного из O центра в точку с s₁ параметром правойчастиспирали Корню, который, например, для данной d = d₁ полуширины Щ щели определён по (10.114) выражению и равен 1_,2, т.е. s₁= 1_,2.

Амплитуда A_1лев вектора A_1лев плоской световой волны линии на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскости с y₀координатой от (рис. 10.31) каждой узкойпрямолинейной элементарной поверхности dS площадью на плоскомволновом фронтесветовой волны S площадью, находящихся левее y₀ координаты и количество которых ограничено, определится длиной вектора (рис. 10.32), направленного из точки с s₁ параметром левойчастиспирали Корнюв

O центр, который, например, для данной d = d₁ полуширины Щ щели определён по (10.114) выражению и равен 1_,2, т.е. s₁= 1_,2.

Результирующая A₁амплитуда вектора A₁ плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d = d₁ полуширины в непрозрачной

Пл плоскости с y₀координатой определится (рис. 10.32) на спирали Корню суммой длины вектора A_1лев, направленного из точки с s₁ параметром в левойчастиспирали Корню в O центр, и длины вектора A_1пр, направленного из O центра в точку с s₁ параметром в правойчастиспирали Корню.

Таким образом, результирующая A₁амплитуда вектора A₁ плоской световой волны линии на Э экране посередине геометрической тени Щ щели с величиной d полуширины в непрозрачной

Пл плоскости с y₀координатой определится (рис. 10.32) на спирали Корню длиной вектора

A₁, направленного из точки с s₁= 1_,2 параметром в левойчастиспирали Корню в точку с

s₁= 1_,2 параметром в правойчастиспирали Корню.

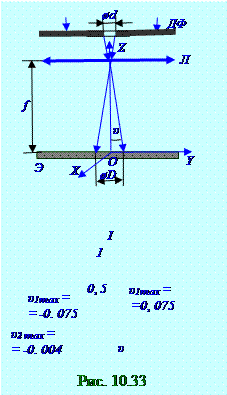
Согласно (рис. 10.32) амплитуда A₁ вектора A₁ плоской световой волны линии на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскости с y₀координатой будет максимальна, т.е. при значении d = d₁ полуширины Щ щели, соответствующей (10.114) равенству параметра s₁спирали Корню величине 1_,2, т.е. s₁= 1_,2, на Э экране напротивсерединыЩ щели I_y₀₁интенсивность монохроматической плоскойсветовой волны будет максимальна.

При (рис. 10.31) увеличении d полуширины Щ щели до значения d = d₂, соответствующей (10.114) равенству параметра s₂спирали Корню(рис. 10.32)величине 2_,8, т.е. s₂= 2_,8, на Э экране напротивсерединыЩ щели I_y₀₂интенсивность монохроматической плоскойсветовой волны будет уменьшенапо сравнению с I_y₀₁интенсивностью монохроматической плоскойсветовой волны при значении d = d₁полуширины Щ щели, соответствующей равенству параметра s₁спирали Корню величине 1_,2, т.е. s₁= 1_,2.

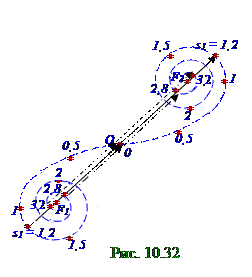
При (рис. 10.31) увеличении d полуширины Щ щели до значения d = d₃, соответствующей (10.114) равенству параметра s₃ спирали Корню(рис. 10.32)величине 3_,2, т.е. s₃= 3_,2, на Э экране напротивсерединыЩ щели I_y₀₃интенсивность монохроматической плоскойсветовой волны будет увеличенапо сравнению с I_y₀₂интенсивностью монохроматической плоскойсветовой волны при значении d = d₂полуширины Щ щели, соответствующей равенству параметра s₂ спирали Корню величине 2_,8, т.е. s₁= 2_,8.

При (рис. 10.31) увеличении d полуширины Щ щели до бесконечногозначения, т. е. при удалении на пути монохроматической плоскойсветовой волныбесконечной непрозрачной Пл плоскости, на Э экране будет существовать I₀интенсивность монохроматической плоскойсветовой волны, которая падает нормальнона этот Э экран.Интенсивность I₀монохроматической плоскойсветовой волны, которая падает нормальнона Э экран, определяют по измерению длины вектора (рис. 10.32), направленного из левого F₁фокуса спирали Корню в правыйF₂фокус этой спирали Корню.

Таким образом, при дифракции Френеля (рис. 10.31) на Э экране посередине геометрической тени Щ щели в непрозрачной Пл плоскостиобразуетсядифракционный максимум0max (m = 0) нулевого порядка при определённых линейных размерах l расстояния Э экрана до непрозрачной Пл плоскости, длины λнормальнопадающей на непрозрачную Пл плоскость световой волныи d полуширины Щ щели с уменьшающейсяинтенсивностьюсветовой волны по мере расширения этой d полуширины Щ щели.

Симметрично (рис. 10.31) с двух сторон дифракционного максимума0 max (m = 0) нулевого порядкапри этих определённых линейных размерах l расстояния Э экрана до непрозрачной Пл плоскости, длины λнормальнопадающей на непрозрачную Пл плоскость световой волныи d полуширины Щ щели образуются дифракционные максимумы1max (m = 1) первого порядкапри y₁ координате, 2 max (m = 2) второго порядкапри y₂координате и т.д. с уменьшающейсяинтенсивностьюсветовой волны по мере увеличения расстояния от этих дифракционные максимумовдо центра Щ щели.

Дифракция Фраунгофера световых волн от круглого отверстия

Монохроматическая плоская световая волна в однородной изотропной среде с

за единицу, и с величиной øD диаметра примерно равного следующему значению: D ≈ f υ₁_min, (10.125) где f - фокусное расстояние Л линзы. Вокруг (рис. 10.33) центрального светлогопятна с величиной øD диаметра располагаются чередующиеся тёмные и светлые кольца. Первый дифракционный минимум образуется под υ₁углом к OZ главнойоптической оси Л линзы, величина которого рассчитывается из следующего выражения: υ₁_min= 1, 22λ/d.(10.126) Выражение (10.126) υ₁_min угла первого дифракционного минимума при дифракции Фраунгофера монохроматической плоской световой волны от круглого отверстия применяется дляследующей оценки дифракционной δθрасходимостипучка света в результате прохождения световой волной с λдлинойволнычерезДФдиафрагмусвеличиной ød диаметра: δθ ~ λ/d. (10.127) Согласно выражению (10.127)монохроматическая плоская световая волна с λдлинойволны после прохождения черезДФдиафрагмусвеличиной ød диаметра перестаёт быть плоской, а лучи световой волны после прохождения через

n показателем преломления, поэтому оптическаяλ= λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.33, падает нормальнона ДФдиафрагму, в котором существует отверстие ød диаметром, намного большим λдлины световой волны, т.е. ød>> λ, а Э экран находится на большом удалении от этого отверстия. В этом случае на Э экране возникает дифракционная картина Фраунгофера, имеющая вид (рис. 10.33) центрального светлогопятна I интенсивности, принятой за

υ₂_max = =0, 004

ДФдиафрагмураспространяютсяв пределах конической поверхности с δθ углом при вершине этого конуса. Величина (10.127) дифракционной δθрасходимостипучка света в результате прохождения световой волной с λдлинойволнычерезДФдиафрагмусвеличиной ød диаметра тем больше, чем меньше этот ød диаметр ДФдиафрагмы.

Дифракция Фраунгофера световых волн от щели в плоскости

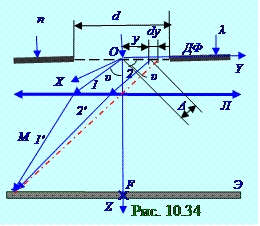
После прохожденияв однородной изотропной среде с n показателем преломления параллельнымпучком световой волны с λдлиной ДФдиафрагмы, имеющей форму (рис. 10.34) щели бесконечной длины по перпендикулярнойплоскости чертежа OX осии dширинойпо OY оси, возникает дифракцияФраунгофера. Каждый элементарныйучасток dy длиной плоской световойволны, находящийся на расстоянии y от центра O щели, согласно принципу Гюйгенса - Френеля

(рис. 10.34), является источником вторичнойсферической волны.

От элементарного(рис. 10.34)участка длиной dy, находящегося в центре щелипо OY оси, в котором находится O начало декартовой OXYZ системы координат,световые лучираспространяютсяв полупространствониже OY оси под всевозможными углами к OZ главной оптической осиЛ линзы и в том числе распространяется 1 луч под υ углом . От элементарногоучастка dy длиной, находящегося на расстоянии y от O центра щели, световой 2 лучтоже распространяетсяпод υ углом, но имеетследующую оптическую Δ разность ходаотносительно 1 луча: Δ = ysinυ. (10.128)

Направим r радиус- векториз (10.8) выражения связи A проекции A светового вектора с

r модулем этого r радиус- вектораиз O центра щели(рис. 10.34) по световому1 лучу. Каждый из лучей,параллельный световому1 лучу, от элементарныхучастков dy длиной на всей ширине

d щели слеваи справа от её O центра на y расстоянии будут иметь следующую Ф_υфазу(10.18)

колебанийdA_υсветового вектора световой волны в произвольный момент t времени в M точке на

Э экране: Ф_υ = ωt - k(r₀+ Δ) + φ,(10.129) где r₀ - оптический путь, проходимый световойволной от элементарногоучастка dy длиной, находящегося в O центре щели, до M точки на Э экране; k = 2π/λ - волновое число, где

λ= λ₀ /n–длинасветовой волны в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ= λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами

на рис. 10.34. Положим начальную Ф_υ0 фазу(10.126) световой волны в M точке на Э экране в момент t₀ = 0 времениот элементарногоучастка dy длиной, находящегося в O центре щели, равной нулю, поэтомус учётом (10.130) равенства нулюоптической Δ₀ разности ходапри y = 0, т.е. Δ₀= 0 выражение φ начальной фазыколебанийA светового вектора монохроматическойплоской световой волны с λдлинойволны после прохождения (рис. 10.34) черезДФдиафрагму принимает следующий вид: Ф_υ0 = ωt₀- k(r₀+ Δ₀) + φ = 0 ↔ φ = kr₀.(10.130) Подставляем (10.128), (10.130) в (10.129) и получаем

следующую зависимость Ф_υфазы колебанийdA_υсветового вектора световой волны в произвольный момент tвремени в M точке на Э экране от любого из элементарныхучастков dy длиной на всей

dширинещелислеваи справа от её O центра на y расстоянии с учётомk = 2π/λволнового числа: Ф_υ = ωt - (2π/λ)ysinυ. (10.131)

Угол υ, под которым падают световыелучи на Э экран от любого из элементарныхучастков dy длиной на всей dширине щели, мал, поэтому A_dyамплитудасветовой волны на Э экране не будет зависетьот направления падения световыхлучей на этот Э экран, т.е. не будет зависеть от υ угла, а будет зависетьтолько от dy длины элементарногоучастка, вследствие чего эта A_dy амплитудасветовой волны на Э экране имеет следующий вид: A_dy = (A_d/d)dy, (10.132) где A_d - амплитуда вектора A светового вектора световой волны на Э экране от всей щели

dшириной; A_d/d - амплитуда A светового вектора световой волны на Э экране от единицы длины щели.

С учётом выражения (10.8) связи Aпроекции A светового вектора с r модулемэтого r радиус- вектора в произвольный момент t времени в M точке на Э экране, т.е. под υ углом (рис. 10.34)

к OZ главной оптической осиЛ линзы, от элементарногоучастка щели dy длиной, а также с учётом (10.132) A_dyамплитудыи (10.133) Ф_υфазыdA_υ модуль dA_υсветового вектора световой волны имеет следующий вид: dA_υ = (A_d/d)dycos[ωt - (2π/λ)ysinυ], (10.133) Модуль A_υ результирующего A светового вектора световой волны в произвольный момент

t времени в M точке на Э экране, т.е. под υ углом (рис. 10.34) к OZ главной оптической оси

Л линзы, от всех элементарныхучастков щели dy длиной с предельнымизначениями y координат, изменяющихся от -d/2 до d/2 величин, имеет следующий вид:

d/2 A_υ =∫(A_d/d)cos[ωt -(2π/λ)ysinυ]dy = [A_dsin(πdsinυ/λ)cosωt]/(πdsinυ/λ). (10.134) -d/2 Амплитуда A_υ_m результирующего A светового вектора световой волны (рис. 10.34) в

M точке на Э экране, т.е. под υ углом к OZ главной оптической осиЛ линзы,с учётом (10.136) выражения имеет следующий вид: A_υ = [A_dsin(πdsinυ/λ)]/(πdsinυ/λ). (10.135) В (рис. 10.34) направлении OZ главной оптической осиЛ линзы, т.е. когда уголυ → 0 и выражен в радианах, с учётом значенияпредела lim(sinυ/υ) = 1 выражение (10.137) принимает следующий вид: A|_{υ → 0} = A_d.(10.136) Согласно (10.136) в направлении OZ главной оптической осиЛ линзы A|_{υ → 0} амплитударезультирующего A_υ светового вектора световой волны в центреЭ экрана равна A_dамплитуде

A светового вектора световой волны на Э экране от всей щелиdшириной.

Интенсивность(10.17) I_υсветовойволны,пропорциональнаквадрату A_υ²амплитуды результирующего A_υ светового вектора световой волны (рис. 10.1.0.34) в M точке на Э экране, т.е. под υ углом к OZ главной оптической осиЛ линзы, поэтому с учётом (10.137) эта интенсивность I_υсветовойволны имеет следующий вид: I_υ = I_dsin²[(πdsinυ)/λ]/[(πdsinυ)/λ]², (10.138) где I_d - интенсивность(рис. 10.1.0.35)световойволны в центреЭ экрана. Дифракционные минимумы1min, т.е. 1-гопорядка,образуются при υ₁_min углах отклонений (рис. 10.1.0.34) плоской световой волны от OZ главной оптической осиЛ линзысогласно (10.137) при k = 1,

При значениях υ угла к главной оптической осиЛ линзы, удовлетворяющих следующему условию: πdsinυ/λ = ± kπ ↔ dsinυ = ± kλ, (10.137) где k = 1, 2, 3, … амплитуда A_υ результирующего A светового вектора световой волны согласно (11.137) обращается в нуль. Следовательно, в (рис. 10.34) направлениях к OZ главной оптической осиЛ линзы, где υ угол удовлетворяет условию (10.139), световые волны от щелиобразуют дифракционные минимумы.

поэтому для этих дифракционных минимумов1min, т.е. 1-гопорядка,выражение(10.139) принимает следующий вид: dsinυ₁_min = ± λ ↔ δυ = 2arcsin(λ/d), (10.139) где δυ - угловая ширинацентрального дифракционного максимума, т.е. угол δυ, выраженный в радианах, между двумя(рис. 10.34) световымилучами, симметричнымиотносительно

OZ главной оптической осиЛ линзы и направленными на дифракционные минимумы

(рис.10.35) 1min, т.е. 1-гопорядка. Учтём в (10.137) свойство тригонометрическойфункции sinυ ≤ 1 для её положительных значений, вследствие чего получим следующее выражение: dsinυ ≤ d ↔ kλ ≤ d ↔ d ≥ kλ, (10.140) где k = 1, 2, 3, …. Согласно (10.140) дифракционные максимумыи минимумыобразуются, когда dширина щелибольше длиныλ волны. В противном случае дифракционные максимумыи минимумыне возникают, а интенсивностьI светамонотонно убывает от середины дифракционнойкартины к её краям. В случае d >> λ, т.е. λ/d << 1 значение arcsin(λ/d) ≈ λ/d, поэтомуугловую ширинуδυ центрального дифракционного максимума с учётом (10.139) определяют согласно следующему выражению: δυ = 2λ/d.(10.141)

Предельный переход от волновой оптики к геометрической

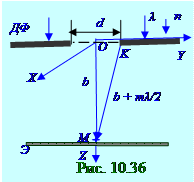
При дифракцииФренеля после прохождения(рис. 10.36) параллельнымпучком световой волны в однородной изотропной среде с n показателем преломленияДФдиафрагмы, имеющей форму щели бесконечной длины по перпендикулярнойплоскости чертежа OX осии d ширинойпо OY оси, эта ДФдиафрагмаоткрывает для M точки на Э экранеm количество зонФренеля, последний

mномеркоторых определяется из следующего выражения для прямоугольногоOMK треугольника: (b + mλ/2)² = b² + (d/2)² ↔ (mλ/2)² + 2b(mλ/2) = d²/4. (10.142) где d/2 - радиус последнейоткрытой для M точки на Э экранезоныФренеля, т.е. имеющейнаибольший m номер открытойзоныФренеля, которая на рис.10.17 обозначена r_m радиусом; λ= λ₀/n– -длинасветовой волны в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ= λ₀/nдлинаэтой световой волны совпадает с геометрическими размерами на рис.10.34.

По аналогии с (10.94), ограничившись рассмотрением не слишком больших mномеровзонФренеля, можно ввиду малости λдлинысветовой волны пренебречь в (10.130) слагаемым, содержащим λ², вследствие чего получается следующее выражение для mномеровзонФренеля: 2b(mλ/2) ≈ d²/4 ↔ m ≈ d²/4λb ↔ m ~ d/(λb)^1/2. (10.143) При количестве m << 1 зонФренеля, что приводит в (10.143) к d << (λb)^1/2выражению, щельнастолько узкая, что открывает малуюдолю (рис. 10.16) 1 - ой зоныФренеля с r₁радиусом. Поэтому дифракцияФренеля отсутствует, т.к. каждый из световыхлучей приходит на Э экран

с различием оптических путейнамного меньших половины λ/2 длины волны.

При: m << 1 ↔ d/(λb)^1/2 << 1 ↔ d << (λb)^1/2(10.144) наблюдается дифракцияФраунгофера на (рис. 10.34), (рис. 10.1.0.36) щели бесконечной длины по перпендикулярнойплоскости чертежа OX осии dширинойпо OY оси с (рис. 10.1.35) ярким центральныммаксимумом и бледнымимаксимумами высшихпорядков.

Если m = 1…5, что приводит в (10.143) к d ≈ (1…5)(λb)^1/2выражению, т.е. щельоткрывает небольшое

количество (рис. 10.16) зонФренеля с r₁, …, r₅радиусами, то на Э экране существует (рис. 10.19), (рис. 10.20) дифракцияФренеляс изображением щели, обрамлённой по краям отчётливо видимыми светлымии тёмнымиполосами. При: m = 1…5 ↔ d/(λb)^{1/ 2}≈ 1…5 ↔ d ≈ (1…5)(λb)^1/2(10.145) наблюдаетсяна Э экране (рис. 10.17), (рис. 10.18) дифракцияФренеляпосередине геометрической тени щели в ДФдиафрагме, обрамлённой по краям отчётливо видимыми светлымии тёмнымиполосами.

Если m >> 1, что приводит в (10.143) к d >>(λb)^1/2выражению, то щельоткрывает большое количество (рис. 10.16)зонФренеля с r₁, r₂, r₃, …радиусами. На Э экране из-за большого

m количества зонФренеляА_m амплитуда световой волныот последней зоны с m номером, будет намного меньше, чем А₁амплитуда световой волныот 1 - ой зоныФренеля с r₁ радиусом из-за того, что расстояние от последней зоныФренеля с m номером будет намного больше расстояния от

Дата добавления: 2016-02-14; просмотров: 678;