Дифракция Фраунгофера[3]от щели

Пусть на очень длинную щель в экране падает плоская волна. Ширина щели b много меньше ее длины b << l. За щелью на очень большом расстоянии L >> b расположен экран. Выясним характер дифракционной картины на экране.

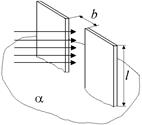Рис. 20.21

Рассмотрим картину в проекции на произвольную горизонтальную плоскость a (рис. 20.21), т.е. как бы «разрежем» щель где-то посередине и будем смотреть на разрез сверху (рис. 20.22).

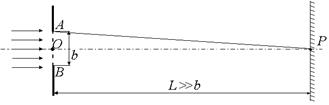
Рис. 20.22

Читатель: По-моему, мы увидим обычную дифракцию Френеля от плоской волны. Мы это уже разбирали.

Автор: Не совсем так. Сейчас экран расположен очень далеко, т.е. так далеко, что в отверстии уложится лишь малая часть первой зоны Френеля. Поэтому из любой точки волновой поверхности АВ лучи придут в точку Р практически в одной фазе. Чтобы было понятнее, рассмотрим конкретный пример. Пусть АВ = 0,2 мм, L = 10 м, l = 500 нм (см. рис. 20.22). Тогда разность хода между лучами ОР и АР составит

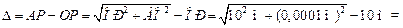
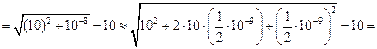
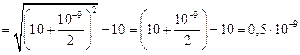м =

= 0,5 нм << l = 500 нм!

Как Вы считаете, что мы увидим в точке Р: максимум или минимум освещенности?

Читатель: Конечно, максимум. Ведь если разбить волновую поверхность АВ на маленькие участки, то все они создадут в точке Р колебания практически в одной фазе. Поэтому если А_i – амплитуда колебаний, создаваемых в точке Р i-м участком, то результирующая амплитуда будет равна сумме этих амплитуд: .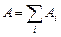

Автор: Вы правы. Теперь давайте выясним, где будет находиться минимум освещенности.

Точнее говоря, выясним, в каком направлении должны распространяться вторичные волны от волновой поверхности АВ (см. рис. 20.22), чтобы давать на экране минимум освещенности. В дальнейшем направления распространения вторичных волн будем для краткости называть лучами, понимая, что это – лучи лишь в чисто геометрическом смысле слова.

Итак, рассмотрим лучи, исходящие от волновой поверхности АВ под углом j к первичному направлению световой волны. Разобьем отрезок АВ (рис. 20.23) на зоны (эти зоны называются зонами Шустера[4]) так, чтобы луч, исходящий из верхней границы зоны «отставал» равно на полволны от луча, исходящего из нижней границы зоны.

Рис. 20.23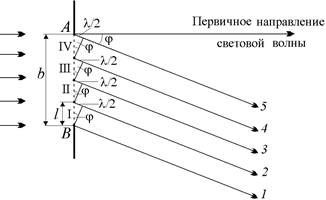

Ясно, что две соседние зоны Шустера будут «гасить» друг друга на экране точно так же, как это происходит с зонами Френеля, поэтому если число зон Шустера при данном угле j четное, то на экране возникнет минимум.

Пусть имеется 2т (т = 1, 2, 3…) зон Шустера, тогда длина l одной такой зоны равна

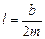, (1)

где b – ширина щели.

Как видно из рис. 20.23, разность хода между лучами, исходящими от границ одной зоны Шустера (например, между лучом 1 и лучом 2), равна

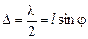. (2)

Подставляя l из (1) в (2), получим

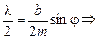
bsinj = ml. (20.14)

Из формулы (20.14) можем определить углы, которые задают направление на минимум освещенности:

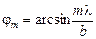. (20.15)

Заметим, что поскольку минимумы должны располагаться симметрично относительно центрального максимума, значения т в формуле (20.15) могут быть как положительными, так и отрицательными целыми числами.

Таким образом, общая картина следующая. При угле j = 0 получаем большой центральный максимум, при углах 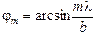, где т = ±1, ±2, …, имеем минимумы освещенности. Ну, а раз есть минимумы, значит, должны быть и максимумы, которые находятся между минимумами.

Ясно, что чем дальше от центра, тем слабее будут максимумы, поскольку в центральном максимуме все колебания возбуждаются в одной фазе, а в остальных (нецентральных) максимумах волны от разных элементов dS_i будут частично «гасить» друг друга, так как между ними всегда будет какая-то разность фаз.

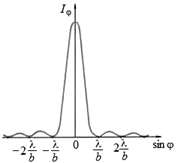Рис. 20.24

На рис. 20.24 показана зависимость интенсивности света (I ~ А²) от синуса угла j.

Читатель: У меня вопрос: если лучи 1 – 5 параллельны (см. рис. 20.23), то как они вообще смогут пересечься на экране в одной точке?

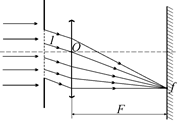Рис. 20.25

Автор: Они почти параллельны (см. рис. 20.22), так как экран очень далеко. Но замечу, есть шанс сделать их строго параллельными. Для этого достаточно поместить сразу за щелью собирающую линзу, а экран поместить в фокальную плоскость этой линзы (рис. 20.25). Через оптический центр линзы луч 1 пройдет, не преломляясь, и пересечется с экраном в побочном фокусе линзы f. Все остальные лучи, параллельные лучу 1, тоже пересекутся в точке f. При этом мы избавимся от необходимости создавать большие расстояния между щелью и экраном, да и дифракционная картина будет более четкой.

Читатель: Да, но тут у меня появилось сомнение: а не изменит ли линза оптическую разность хода лучей? Ведь ясно, что при прохождении линзы оптическая длина пути каждого луча меняется… И если у всех она изменится по-разному, то линза «испортит» всю картину.

Автор: Ваше опасение не лишено оснований, но могу Вас заверить, линза обладает тем свойством, что если «лучи» упали на ее поверхность в одной фазе, то после пересечения за линзой они тоже будут иметь одинаковую фазу. Строгое доказательство этого факта мы опустим, но соображение качественного характера приведем.

Пусть лучи 1 и 2 упали на собирающую линзу, как показано на рис. 20.26, а после преломления пересеклись в точке F. Пусть в точках М и N у лучей были равные фазы.

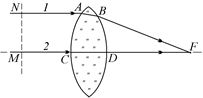Рис. 20.26

Оптическая длина пути луча 1 равна

L₁ = MC + n×CD + DF.

Оптическая длина пути луча 2 равна

L₂ = NA + n×AB + BF.

Здесь п – показатель преломления материала линзы.

Из рис. 20.26 видно, что MC + DF < NA + BF, но зато CD > AB, т.е. луч 2 прошел больший путь на воздухе, но зато меньший в стекле. Поэтому оптические пути L₁ и L₂ вполне могут быть равны. (Строго доказать это можно, например, с помощью принципа наименьшего времени Ферма, о котором мы здесь рассказывать не будем.)

Задача 20.2. На щель шириной b = 20 мкм падает нормальный параллельный пучок монохроматического света (l = 500 нм). Найти ширину Dх изображения щели на экране, удаленном от щели на расстояние l = 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности.

b = 20 мкм l = 500 нм l = 1 м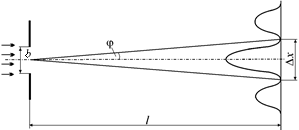
Dх = ?
Рис. 20.27

Решение. Из рис. 20.27 видно, что . Поскольку угол j мал, то можно принять tgj = sinj. Тогда

Dх = 2lsinj. (1)

Условие минимумов интенсивности света bsinj = тl, откуда при т = 1

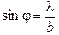. (2)

Подставляя (2) в (1), получим

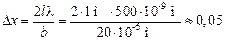м = 5 см.

Ответ: 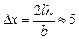см.

СТОП! Решите самостоятельно: А2, В7, С4.