Дифракционная решетка
Спектральный прибор – что это такое? Рассмотрим ситуацию: некоторый источник излучает свет, волны которого имеют длины l1, l2, …, lп. Нас интересует, во-первых, сколько разных волн содержится в излучаемом свете; во-вторых, каковы (хотя бы приблизительно) цвета этих волн; и в-третьих, какова (это, конечно, в идеале) длина каждой волны.
Ясно, что для решения этой задачи нужен прибор, который разделял бы волны разных длин. Причем разделял бы таким образом, чтобы по величине отклонения луча света с той или иной длиной волны можно было бы вычислить длину волны света (рис. 20.28).
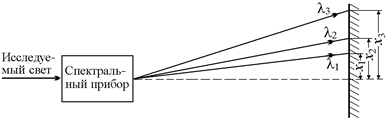
Рис. 20.28
Прибор такого типа называется спектральным. Простейший спектральный прибор – это призма, которой пользовался Ньютон при изучении дисперсии света. Призма как бы «разворачивает» белый свет в спектр.
Еще одним спектральным прибором является дифракционная решетка, которая представляет собой множество очень узких длинных щелей, расположенных друг за другом в ряд через некоторые промежутки. Чисто практически дифракционная решетка – это стеклянная пластина, на которую нанесены очень тонкие параллельные штрихи (до одной тысячи на 1 мм) (рис. 20.29).
 Рис. 20.29
Рис. 20.29
|
Дифракционная решетка характеризуется тремя основными параметрами: шириной щели b, шагом решетки (расстоянием между соседними щелями) d и общим числом щелей N (20.30).
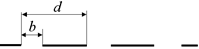
Рис. 20.30
Дифракционной решеткой можно пользоваться так же, как одной узкой щелью: на решетку должна падать плоская световая волна (которую можно создать с помощью собирающей линзы, если разместить источник света в главном фокусе), а дифракционную картину надо наблюдать либо на сильно удаленном экране, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис. 20.31).
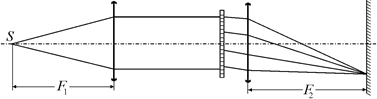
Рис. 20.31
Какую дифракционную картину дает дифракционную решетка? Наверное, очевидно, что если одна щель дает дифракционную картину (см. рис. 20.24), то N щелей тоже дадут какую-то дифракционную картину. Причем из-за интерференции между световыми волнами, проходящими через различные щели, картина должна получиться более сложной.
Начнем с самого простого: что мы увидим в точке О на экране, находящемся на оси симметрии решетки (рис. 20.32)?
Рис. 20.32 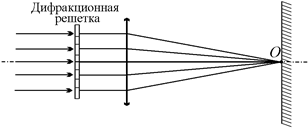
Читатель: Очевидно, максимум амплитуды, так как все лучи, идущие от решетки на линзу, имеют нулевую разность фаз.
Автор: Конечно! Этот максимум мы назовем центральным. А где будут находиться на экране минимумами освещенности?
Читатель: Мы выяснили, что каждая щель дает минимум в направлениях, которые задаются уравнением
bsinj = тl, (20.16)
где т = ±1, ±2, …, а j – угол между направлениями луча на «точку минимума» и осью симметрии системы (рис. 20.33). Я думаю, что если каждая из N щелей решетки дает в этих направлениях ноль, то и все щели вместе тоже дадут ноль! То есть в тех точках на экране, направление на которые задается углами:
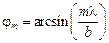 , (20.17)
, (20.17)
где т = ±1, ±2, … , наблюдается минимум освещенности.
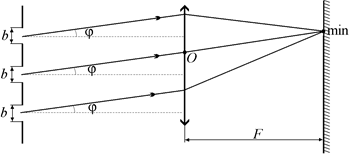 Рис. 20.33
Рис. 20.33
Автор: Вы правы. Но, забегая вперед, скажу, что только этими минимумами дело не кончится. Поэтому назовем минимумы, определяемые формулой (20.17), главными.
Теперь подумаем, по каким направлениям будут наблюдаться максимумы. Рассмотрим две соседние щели. Разобьем волновые поверхности в этих щелях на узкие полоски площадью dSi каждая и рассмотрим два луча, выходящих под углом j от нижних краев каждой щели (рис. 20.34). Опустим перпендикуляр из точки В на луч 1 и получим треугольник АВС.
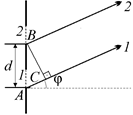 Рис. 20.34
Рис. 20.34
|
Оптическая разность хода лучей 1 и 2 равна отрезку АС = АВsinj = dsinj. Для того чтобы происходило усиление колебаний, волны, идущие в направлениях 1 и 2, должны иметь оптическую разность хода, равную целому числу длин волн:
dsinj = kl, (20.18)
где k = ±1, ±2, …
Читатель: Да, но разные лучи, исходящие только из щели 1 в направлении j, будут иметь разные оптические разности хода. Например, может быть и такое, что луч, исходящий из нижней точки щели, «отстанет» от луча, исходящего от верхней точки щели на l/2 (рис. 20.35). Тогда в рамках одной щели эти лучи будут гасить друг друга!
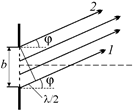 Рис. 20.35
Рис. 20.35
| Автор: Согласен! Но совокупное действие всех этих лучей в рамках одной щели (если только bsinj ¹ тl!) все-таки положительное: раз щель в целом не дает на экране ноль, значит, она дает какую-то амплитуду (пусть и не очень большую за счет того, что частично волны от одной щели гасят друг друга). |
Тогда при угле j, определенным уравнением (20.18) все эти амплитуды, создаваемые каждой щелью, как целым, будут складываться. И мы получим явный максимум освещенности, который будет тем больше, чем больше число N – число щелей в дифракционной решетке! Эти максимумы мы назовем главными.
Читатель: Хорошо! Но ведь главный максимум может случайно «наехать» на главный минимум. Ну, например, если d = 2b,по формуле (20.18) получим:2bsinj = kl. Если k – четкое, т.е. k = 2т, получим 2bsinj = 2тl Þ bsinj = тl – а это условие главного минимума (формула (20.16))!
Автор: Вы совершенно правы! Если такое случится, то все четные главные максимумы «пропадут»! Вообще, если отношение b/d представляет собой простую дробь b/d = k/m, где k и т – целые (k < m), то обязательно произойдет «пропажа» каких-то главных максимумов.
Теперь давайте еще раз обратимся к минимумам. Оказывается, кроме главных, существуют еще огромное количество так называемых дополнительных минимумов.
Читатель: А откуда же они берутся?
Автор: Да, за счет интерференции между щелями, ведь раз в определенных направлениях щели «могут» усиливать друг друга, значит, в каких-то других направлениях они могут друг друга и «гасить».
Но прежде чем мы продолжим разговор о дифракционной решетке, вспомним, как можно графически сложить гармонические колебания одинаковой частоты, отличающейся друг от друга по фазе[5].
Пусть в некоторой точке складываются два колебания:
x1 = acoswt, (1)
x2 = acos(wt +a). (2)
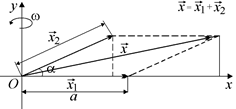 Рис. 20.36
Рис. 20.36
|
Изобразим на координатной плоскости вектор 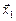 совпадающим в начальный момент с осью х, а вектор
совпадающим в начальный момент с осью х, а вектор 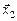 – повернутым относительно оси х на угол a (рис. 20.36). Модули обоих векторов равны а. Если векторы
– повернутым относительно оси х на угол a (рис. 20.36). Модули обоих векторов равны а. Если векторы 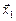 и
и 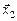 будут вращаться около начала координат с угловой скоростью w, их проекции на ось х будут изменяться по законам (1) и (2). Тогда результирующее колебание
будут вращаться около начала координат с угловой скоростью w, их проекции на ось х будут изменяться по законам (1) и (2). Тогда результирующее колебание
х(t) = x1(t) + x2(t) (3)
можно изобразить вектором, равным сумме векторов 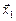 и
и 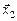 , вращающимся около точки О со скоростью w: проекции этого вектора на ось х в каждый момент времени будут определяться выражением (3).
, вращающимся около точки О со скоростью w: проекции этого вектора на ось х в каждый момент времени будут определяться выражением (3).
Итак, модуль вектора 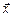 можно найти графически как векторную сумму векторов
можно найти графически как векторную сумму векторов 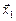 и
и 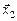 в момент времени t = 0:
в момент времени t = 0:
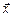 =
= 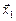 +
+ 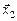 .
.
Теперь допустим, что нам надо сложить п колебаний одинаковой амплитуды а и частоты w, причем каждое последующее колебание опережает предыдущее по фазе на a.
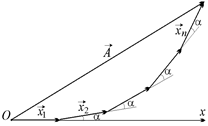 Рис. 20.37
Рис. 20.37
|
Каждое колебание представим вектором 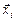 с одним и тем же модулем а, составляющим с осью х угол 0; a; 2a; 3a; …, (п –1)a; … соответственно. Результирующее колебание может быть представлено векторной суммой этих п векторов, причем модуль результирующего колебания будет равен модулю результирующего вектора
с одним и тем же модулем а, составляющим с осью х угол 0; a; 2a; 3a; …, (п –1)a; … соответственно. Результирующее колебание может быть представлено векторной суммой этих п векторов, причем модуль результирующего колебания будет равен модулю результирующего вектора 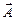 (рис. 20.37).
(рис. 20.37).
А теперь скажите: каким должен быть угол a, чтобы при сложении п таких колебаний мы получили нулевой вектор 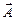 ?
?
Читатель: По-моему, ясно, что если п = 2, то a = p, если п = 3, 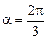 , если п = 4,
, если п = 4, 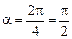 и т.д. В общем случае
и т.д. В общем случае 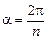 (рис. 20.38).
(рис. 20.38).
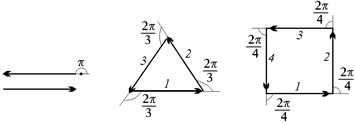
Рис. 20.38
Автор: Вы правы! Но заметьте, если поворачивать каждый последующий вектор не на  , а на k
, а на k  , где k < n, т.е. на
, где k < n, т.е. на 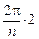 ,
, 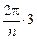 ,
, 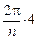 и т.д., то общий поворот при последовательном переходе от первого вектора ко второму, от второго к третьему и т.д., … от предпоследнего к последнему и от последнего к первому составит (за п поворотов) соответственно 4p, 6p, 8p и т.д., т.е. векторы опять-таки составят замкнутую фигуру, и их суммой будет нулевой вектор. На рис. 20.39 показан случай п = 3, k = 2.
и т.д., то общий поворот при последовательном переходе от первого вектора ко второму, от второго к третьему и т.д., … от предпоследнего к последнему и от последнего к первому составит (за п поворотов) соответственно 4p, 6p, 8p и т.д., т.е. векторы опять-таки составят замкнутую фигуру, и их суммой будет нулевой вектор. На рис. 20.39 показан случай п = 3, k = 2.
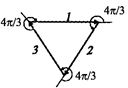 Рис. 20.39
Рис. 20.39
|
Итак, сделаем важный вывод: при суммировании п колебаний с одинаковой амплитудой результирующее колебание имеет нулевую амплитуду (или, иными словами, колебания «гасят» друг друга), если фаза каждого последующего колебания отличается от фазы предыдущего на k  , где k = 1, 2, 3, …, п – 1.
, где k = 1, 2, 3, …, п – 1.
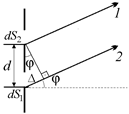 Рис. 20.40
Рис. 20.40
|
Теперь вернемся к дифракционной решетке. Рассмотрим лучи, идущие от малых одинаковых участков dS1 и dS2, расположенных у краев двух соседних щелей в направлении, составляющем угол a с осью симметрии (рис. 20.40). Пусть угол j таков, что оптическая разность хода лучей 1 и 2 равна:
 ,
,
где k = 1, 2, 3, …, N – 1; N – число щелей в решетке.
Тогда колебания, которые возбудят эти два луча в точке, в которой они сойдутся на экране, будут отличаться по фазе на k 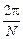 . От N щелей выйдут N таких колебаний. Эти колебания будут иметь одинаковую амплитуду, и каждое последующее будет опережать по фазе предыдущее на
. От N щелей выйдут N таких колебаний. Эти колебания будут иметь одинаковую амплитуду, и каждое последующее будет опережать по фазе предыдущее на 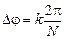 . Поэтому (как мы только что доказали) результирующее колебание будет иметь нулевую амплитуду.
. Поэтому (как мы только что доказали) результирующее колебание будет иметь нулевую амплитуду.
Для каждого малого участка dSi одной щели найдутся (N – 1) соответствующих участков в остальных (N – 1)-й щелях, которые возбудят в указанном направлении колебания, которые «погасят» друг друга. Поэтому можно утверждать, что в указанном направлении будет наблюдаться минимум освещенности.
Заметим, что если разность хода лучей 1 и 2 будет равна не k 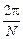 , а k
, а k 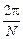 ±l, k
±l, k 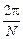 ±2l, …, k
±2l, …, k 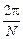 ±тl, где т = ±1, ±2, …, то это будет означать, что разность фаз соответствующих колебаний будет равна: k
±тl, где т = ±1, ±2, …, то это будет означать, что разность фаз соответствующих колебаний будет равна: k 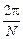 ±2p, k
±2p, k 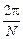 ±4p, …, k
±4p, …, k 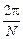 ±2pт. Ясно, что «добавка» (2pт) никак не изменит ситуацию и в данных направлениях тоже будут наблюдаться минимумы.
±2pт. Ясно, что «добавка» (2pт) никак не изменит ситуацию и в данных направлениях тоже будут наблюдаться минимумы.
Таким образом, мы можем утверждать, что минимумы освещенности будут наблюдаться в направлениях, определяемых уравнением:
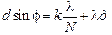 ,
,
где k = 1, 2, 3, …, (N – 1). Заметим, что k и т не могут одновременно равняться нулю, так как j = 0 – это условие центрального максимума, кроме того, k ¹ N, поскольку в этом случае 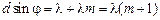 , а это условие главного максимума.
, а это условие главного максимума.
Подведем итоги по максимумам и минимумам освещенности, которые выведем в виде таблицы:
| Центральный максимум | j = 0 | ||
| Главные максимумы | dsinj = тl | т = ±1, ±2,… | |
| Главные минимумы | bsinj = kl | k = ±1, ±2,… | |
| Дополнительные минимумы | 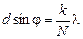 +тl +тl
| т = 0, ±1, ±2,… k = 1, 2,…, (N–1) |
Теперь посмотрим, как выглядит график зависимости интенсивности света от величины j, если на решетку падает монохроматический свет (рис. 20.41). В этой решетке главные минимумы «не наезжают» на главные максимумы.
Рис. 20.41 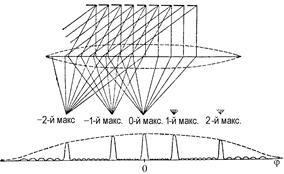
На рис. 20.42 показан график зависимости интенсивности света от величины sinj для N = 4 и d/b = 3. Пунктирная кривая, проходящая через вершины главных максимумов, изображает интенсивность от одной щели, умноженную на N2. При взятом на рисунке отношении периода решетки к ширине щели (d/b= 3) главные максимумы 3-го, 6-го и т.д. порядков приходятся на минимумы интенсивности от одной щели, вследствие чего эти максимумы пропадают.
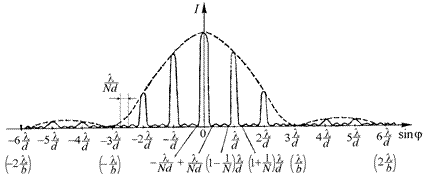
Рис. 20.42
Читатель: А почему интенсивность света в главных максимумах в N2 раз больше интенсивности света от одной щели?
Автор: В главных максимумах складываются амплитуды каждой щели в данном направлении, поэтому амплитуда в главном максимуме Аmax = NA1, где А1 – амплитуда от одной щели. Поскольку интенсивность света (освещенность) I ~ А2, то
Imax = (NA1)2 = 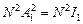 ,
,
где I1 – интенсивность света от одной щели в данном направлении. Теперь давайте подумаем, каким должен быть шаг решетки (величина d), чтобы решетка «работала» наилучшим образом.
Читатель: Я думаю, надо исходить из того, что главные максимумы (кроме центрального, конечно) должны для разных волн находиться подальше друг от друга.
Автор: Верно!
Читатель: Условия главного максимума
dsinj = kl 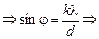
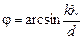 .
.
Значит, для волны l1 k-й главный максимум будет при угле j1:
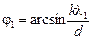 ,
,
а для волны l2 – при угле j2:
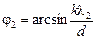 .
.
Если углы не очень велики, то arcsinx » x, поэтому «угловое расстояние» между главными максимумами примерно равно
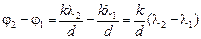 .
.
Ясно, что чем меньше d, тем больше Dj1. Следовательно, d должно быть как можно меньшим!
Автор: Согласен! Но здесь нельзя переусердствовать, ведь 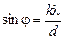 . Если d < kl, то sinj > 1! Это значит, что при таком маленьком шаге решетки главного максимума даже первого порядка мы не получим!
. Если d < kl, то sinj > 1! Это значит, что при таком маленьком шаге решетки главного максимума даже первого порядка мы не получим!
Теперь давайте подумаем, каким стоит взять N – количество щелей: большим или малым?
Читатель: Я думаю, что чем больше, тем лучше, ведь в главных максимумах складываются амплитуды колебаний отдельных щелей. Следовательно, чем больше N, тем ярче картина!
Автор: Согласен. Но есть и еще одно обстоятельство в пользу увеличения N.
Если допустить, что sinj » j, то, как видно из рис. 20.42, «угловое расстояние» между ближайшими главными максимумами равно 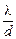 , а между ближайшими дополнительными минимумами
, а между ближайшими дополнительными минимумами 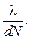
«Угловое расстояние» Dj между двумя дополнительными минимума, стоящими слева и справа от любого главного максимума, таким образом, равно:
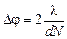 . (20.19)
. (20.19)
Увеличивая N, мы согласно формуле (20.19), можем сделать Dj сколь угодно малым! А это значит, что т-й главный максимум будет сколь угодно узким: ведь этот максимум как бы «зажат» между двумя дополнительными минимумами!
А теперь скажите, что мы увидим, если направим на дифракционную решетку белый свет?
Читатель: Я думаю, мы увидим такой же спектр, как в опыте Ньютона с призмой.
Автор: Почти такой же, разница в том, что призма сильнее всего преломляла «лучи» с короткими волнами (фиолетовый цвет), а дифракционная решетка лучше всего отклоняет длинные волны (красный цвет).
Читатель: А не могут ли при этом главные максимумы разных порядков «наехать» друг на друга?
Автор: Могут! Волны l1 и l2 будут иметь максимумы разных порядков в одном месте, если будет выполняется равенство
dsinj = l1k = l2(k + 1)!
На рис. 20.43 схематически показано, как спектры белого цвета разных порядков налагаются друг на друга.
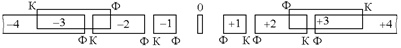
Рис. 20.43
СТОП! Решите самостоятельно: А3, В8, В9, С5.
Задача 20.3. Дифракционная решетка содержит 120 штрихов на 1,00 мм. Найти длину волны монохроматического света, падающего на решетку, если угол между двумя спектрами первого порядка равен 8,00°.
| k = 1 N = 120 l = 1,00 мм Dj = 8,00° | Решение. Заметим, что в литературе вместо того, чтобы сказать «главный максимум» иногда употребляют не совсем подходящее в данной ситуации слово «спектр». Именно так обстоит дело в данном случае. Направление на главный максимум первого порядка определяется формулой (20.18) |
| l = ? | |
dsinj = 1×l. (1)
Шаг решетки, очевидно, равен
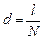 . (2)
. (2)
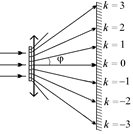 Рис. 20.44
Рис. 20.44
|
Угол Dj между направлением на спектры (т.е. максимумы) первого порядка равен 2j (рис. 20.44):
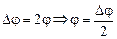 . (3)
. (3)
Подставляя (2) и (3) в (1) получим:
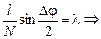
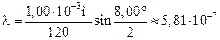 м = 581 нм.
м = 581 нм.
Ответ: 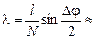 581 нм.
581 нм.
СТОП! Решите самостоятельно: А5, В10–В12, С6.
Задача 20.4. Определить наибольший порядок спектра, который может образовать дифракционная решетка, имеющая 500 штрихов на 1 мм, если длина волны падающего света 590 нм. Какую наибольшую длину волны можно наблюдать с помощью решетки?
| N = 500 l = 1 мм l = 590 нм | Решение. Условие главного максимума имеет вид dsinj = lk, где
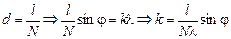 .
Ясно, что максимально возможное значение k соответствует максимальному значению sinj: .
Ясно, что максимально возможное значение k соответствует максимальному значению sinj:
|
| kmax = ? lmax = ? | |
sinj = 1 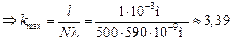 .
.
Но поскольку kmax может быть только целым числом, то kmax = 3.
Итак, при длине волны 590 нм мы увидим на экране главные максимумы 1-го, 2-го и 3-го порядков.
Теперь ответим на второй вопрос: какую наибольшую длину волны можно наблюдать в этой решетке? Иными словами, надо определить, при какой наибольшей длине волны ее главный максимум (неважно какого порядка) можно будет увидеть на экране.
Из условия главного максимума длина волны равна 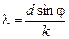 . Ясно, что l будет максимальна, если k = 1 и sinj = 1. Тогда
. Ясно, что l будет максимальна, если k = 1 и sinj = 1. Тогда
 2000 нм.
2000 нм.
Читатель: Но максимальная длина волны видимого света всего 760 нм!
Автор: Вы правы: свет с длиной волны 2000 нм – это уже не свет в прямом смысле этого слова, а инфракрасное излучение, о котором речь еще впереди, так что увидеть мы сможем лишь видимый (красный) свет с наибольшей длиной волны 760 нм.
Ответ: kmax = 3, l = 760 нм.
СТОП! Решите самостоятельно: А6, В13, С7, С8.
Задача 20.5. На дифракционную решетку с периодом d = 14 мкм падает нормально монохроматическая световая волна. На экране, удаленном от решетки на L = 2,0 м, расстояние между спектрами второго и третьего порядка s = 8,7 см. Какова длина волны l падающего света?
| d = 14 мкм L = 2,0 м s = 8,7 см | 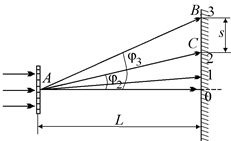 Рис. 20.45 Рис. 20.45
|
| l = ? | |
Решение. В данном случае наблюдение проводится без помощи собирающей линзы на удаленном экране (рис. 20.45).
Надо сказать, что без линзы главные максимумы будут достаточно «размытыми» по экрану, а «ширина» каждого главного максимума будет примерно равна размерам дифракционной решетки. Но если размеры решетки всего несколько миллиметров, то в условиях данной задачи можно считать решетку точкой А (см. рис. 20.45). Тогда расстояние между 2-м и 3-м максимумами – это отрезок ВС. Условия этих главных максимумов имеют вид:
dsinj2 = 2l, (1)
dsinj3 = 3l. (2)
Из DАОВ
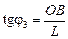 , (3)
, (3)
из DАОС
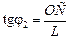 , (4)
, (4)
S = ВC = OB – OС. (5)
Учитывая, что s << L, тангенсы в формулах (3) и (4) можно заменить синусами, так как при малых a tga » sina. Тогда, вычитая из уравнения (3) уравнение (4), получим:
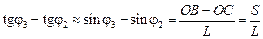 . (6)
. (6)
Вычитая из уравнения (2) уравнение (1), получим:
d(sinj3 – sinj2) = 3l – 2l Þ
sinj3 – sinj2 = l/d. (7)
Приравняем правые части уравнений (6) и (7), получим:
 м.
м.
Ответ: 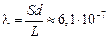 м.
м.
СТОП! Решите самостоятельно: А7, В14, В15, С9.
Задача 20.6.Перпендикулярно поверхности дифракционной решетки падают параллельные лучи света от некоторого источника. Линия с l1 = 6,6×10–7 м видна в спектре второго порядка (k1 = 2) под некоторым углом j. Какие еще спектральные линии будут видны под этим же углом (принять диапазон видимого света от 4,0×10–7 м до 7,0×10–7 м)?
| l1 = 6,6×10–7 м k1 = 2 lmax = 4,0×10–7 м lmin = 7,0×10–7 м | Решение. Волна l1 = 6,6×10–7 м – это достаточно длинная волна (красный цвет), поэтому ее главный максимум 2-го порядка один из наиболее удаленных от центрального максимума в данном спектре (см. рис. 20.43). «Наехать» на главный максимум этой волны может только ка- |
| l2 = ? | |
кой-нибудь главный максимум 3-го порядка более короткой волны, т.е. должно выполняться равенство:
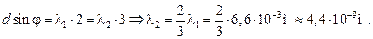
Эта длина волны соответствует фиолетовому цвету.
Ответ: 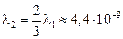 м.
м.
СТОП! Решите самостоятельно: В16, С10.
Дата добавления: 2016-04-11; просмотров: 3630;
