Дифракция и поляризация света

Задача 10.1

На дифракционную решётку нормальноеё поверхности падает монохроматический свет с λ₀ длиной волны в вакууме, равной 650 нм. За этой дифракционной решёткой находится Л линза, в фокальнойплоскости которой находится Э экран. На этом Э экране наблюдается дифракционный максимум под υ_maxλ0 угломдифракции, который равен 30˚ . При каком f фокусном расстоянии Л линзы линейнаяD_л дисперсия дифракционной решётки равна

0,5 мм/нм?

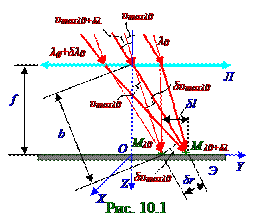
m -го порядка (10.161) из раздела 10.2 "Дифракция света"при изменении λ₀ длинысветовой волны в вакууме на δλ₀величину, а также с учётом(1.1) длины b оптического путиотЛ линзы до Э экрана светового лучас λ₀ длиной волны это расстояние δr междусветовым лучомс λ₀ длиной волны и световым лучомс λ_{0 +} δλ длиной волны имеет следующий вид: δr ≈ bδυ = fδυ/cosδυ_maxλ0 .(1.2)Элементарное(рис. 10.1) δlприращение линейного отклонениянаЭ экране дифракционного максимума m -го порядкапри изменении λ₀ длины световой волны на δλ₀величину с учётом (1.2) расстояния δr междусветовым лучомс λ₀ длиной волны и световым лучомс λ_{0 +} δλ длиной волны имеет следующий вид: δl = δr/cosυ_maxλ0 = fδυ/cos²υ_maxλ0.(1.3)Подставляем (1.3) элементарное(рис. 10.1) δlприращение линейного отклоненияна

Э экране дифракционного максимума m -го порядкапри изменении λ₀ длины световой волны на

δλ₀величину в выражение (10.193) из раздела 10.2 "Дифракция света" и получаемследующее выражениеD_ллинейной дисперсии дифракционной решётки: D_л = δl/δλ₀ = (f/cos²υ_maxλ0)δυ/δλ₀ ↔ f = D_л(δλ₀/δυ)cos²υ_maxλ0 .(1.4) Подставляем (1.4) линейнуюD_л дисперсию дифракционной решётки в выражение (10.196) из раздела 10.2 "Дифракция света " угловой дисперсииэтой дифракционной решётки

D_у = δυ/δλ и получаем следующее выражение f фокусного расстояния Л линзы:

f = (D_лcos²υ_maxλ0)/D_у. (1.5)Подставляем в (1.5) f фокусное расстояние Л линзы выражение (10.193) из раздела 10.2 "Дифракция света" угловой дисперсииD_у = m/(hcosυ_max) дифракционной решётки и получаем следующее выражение для этого f фокусного расстояния Л линзы, в котором все параметрыявляются известными из условия кроме m порядкадифракционного максимумаи h расстояния (рис. 10.37) из раздела 10.2 "Дифракция света" между щелями или постоянной дифракционной решётки: f = (D_лhcos³υ_maxλ0)/m.(1.6)Используем выражение (10.162) из раздела 10.2 "Дифракция света" |sinυ_max| = mλ/h для определения отношения расстояния h между щелями или постоянной дифракционной решётки к m порядкудифракционного максимума, наблюдаемого (рис. 10.1) наЭ экране, которое имеет следующий вид: h/m = λ₀ /sinυ.(1.7)Подставляем (1.7) h/m отношение расстояния h между щелями к m порядкудифракционного максимума в выражение (1.6) и получаем следующее выражение для f фокусного расстояния Л линзы, в котором все параметры в правойчастиявляются известными из условия: f = (D_лλ₀cos³υ_maxλ0)/sinυ_{maxλ0 ≈} 43 см.(1.8) При выполнении f фокусного расстояния Л линзы согласно (1.8) наблюдение дифракционногомаксимума m -го порядка будет осуществляться под углом υ_maxλ0 дифракции к главной оптической (рис. 10.1) OZ оси, если на дифракционную решётку, имеющую заданную D_л линейную дисперсию, нормальноеё поверхности падает монохроматический свет с λ₀ длиной волны в вакууме.

Задача 10.2

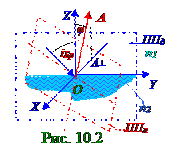
ИнтенсивностьI(10.17) из раздела 10.1 "Электромагнитная природа света. Интерференция света" падающей световойволны пропорциональна квадратуамплитуды A (рис. 10.2.1.2) вектора A плоской световой волны, т.е.интенсивностьI связана с амплитудой A вектора A плоской световой волны следующим соотношением: I = kA², (2.1) где k – коэффициент пропорциональности между Iинтенсивностью и амплитудой A вектора A падающей световой волны.

Падающая световаяволна плоско - поляризована в ПП_л плоскости поляризации, составляющей φ угол с ПП_д плоскостью падения этой световой волны, поэтому вектор A плоской световой волны, находящийся в ПП_л плоскости поляризации, имеет проекцию A_┴ на OX ось, т.е. на перпендикуляр к поверхности ПП_д плоскости падения, имеющий следующий вид: A_┴ = Asinφ.(2.2)

ИнтенсивностьI_┴ (10.17) из раздела 10.1 "Электромагнитная природа света. Интерференция света" падающей световойволны, которая поляризованав плоскости, перпендикулярной к поверхности ПП_д плоскости падения, с учётом (2.2) проекции A_┴ на OX ось световойволны, которую можно считать модулем вектора A_┴ падающей световой волны, перпендикулярного к поверхности ПП_д плоскости падения, имеет следующий вид: I_┴ = kA_┴² = k A²sin²φ ↔ kA² = I_┴/sin²φ. (2.3) где k – коэффициент пропорциональности между I_┴ интенсивностью падающей световойволны, которая поляризованав плоскости, перпендикулярной к поверхности ПП_д плоскости падения, и амплитудой A вектора A этой падающей световойволны.

Подставляем (2.3) в (2.1) и получаем следующее соотношение между Iинтенсивностьюпадающей световойволны и I_┴ интенсивностьюпадающей световойволны, которая поляризованав плоскости, перпендикулярной к поверхности ПП_д плоскости падения: I = I_┴/sin²φ. (2.4)

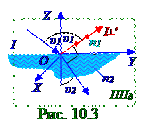
Согласно условию задачи υ₁ угол падения(рис. 10.2.1.3) световых лучей равен i_Бр углу Брюстера (10.219) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом", т.е. υ₁ = i_Бр, поэтому выполняется следующее соотношение: tgυ₁ = n₂/n₁ = n₂₁, (2.5) где n₂₁ - показатель n₂ преломления водыотносительно показателя n₁ преломления воздуха.

Согласнозакону Снеллиуса (9.104) из раздела 9.0 " Электромагнитные волны. Излучение"имеем следующее выражение, связывающее (рис. 10.3) υ₁ угол падения и υ₂ уголпреломления световых лучей: sinυ₁/sinυ₂ = n₂/n₁ = n₂₁. (2.6) Совместное решение (2.5), (2.6) относительно υ₁ угла падения и υ₂ углапреломления световых лучейприводитк следующему выражению:

tgυ₁ = n₂₁ sinυ₁/cosυ₁= n₂₁ ↔ cosυ₁ = sinυ₂ ↔ cosυ₁ =cos[(π/2) - υ₂] ↔

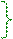
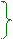sinυ₁/sinυ₂ = n₂₁ ↔ sinυ₁/sinυ₂ = n₂₁

↔ υ₁ = (π/2) - υ₂ ↔ υ₁ + υ₂ = π/2. (2.7)

Согласно (2.7) при (рис. 10.3) падении световых лучей под i_Бр углом Брюстера отражённые световые лучисI_┴′ интенсивностью, которые поляризованыв плоскости, перпендикулярной к поверхности ПП_д плоскости падения, перпендикулярны преломлённым световым лучам.

Коэффициент ρ отражения световой волны - это отношение отражённых световых лучейсI_┴′ интенсивностью, поляризованныхв плоскости, перпендикулярной к поверхности ПП_д плоскости падения,к падающей световойволныс I интенсивностью, имеющее следующий вид: ρ = I_┴′/I. (2.8)

Подставляем (2.4) соотношение между Iинтенсивностьюпадающей световойволны и

I_┴ интенсивностьюпадающей световойволны, которая поляризованав плоскости,

коэффициентом ρ_┴ отражениялинейно - поляризованной световой волны в плоскости, перпендикулярной к поверхности ПП_д плоскости падения.

С учётом (2.7) равенства суммы υ₁ угла падения и υ₂ углаотражения световых лучей при

(рис. 10.3) падении световых лучей под i_Бр углом Брюстеравеличинеπ/2, т.е. υ₁ + υ₂ = π/2, выражение ρ_┴ = sin²(υ₁ - υ₂)/ sin²(υ₁ + υ₂)коэффициента ρ_┴ отражениялинейно - поляризованной световой волны в плоскости, перпендикулярной к поверхности ПП_д плоскости падения, принимает следующий вид: ρ_┴ = sin²(υ₁ - υ₂). (2.10)

Подставляем (2.10) в (2.9) и получаем следующее выражение коэффициента ρ отражения световой волны, равное отношению отражённыхсветовых лучейсI_┴′ интенсивностьюк падающей световойволныс I интенсивностью, как функцию υ₁ угла падения, υ₂ углаотражения световых лучейи (рис. 10.2) φ угла ПП_л плоскости поляризации с ПП_д плоскостью падения этой световой волны: ρ = sin²(υ₁ - υ₂)sin²φ. (2.11) Проводим тождественные тригонометрические преобразования с sin²(υ₁ - υ₂) выражением в (2.11), вследствие чего это sin²(υ₁ - υ₂) с учётом (2.7) υ₁ = π/2 - υ₂ принимает следующий вид: sin²(υ₁ - υ₂) = {1 -[2/(1 + tg²υ₁)]}².(2.12)

Подставляем (2.12) в (2.11) с учётом tgυ₁ = n₂₁ при (рис. 10.3) падении световых лучей под i_Бр = υ₁ углом Брюстераи получаем следующее окончательное выражение коэффициента ρ отражения световой волны, равное отношению отражённыхсветовых лучейсI_┴′ интенсивностьюк падающей световойволныс I интенсивностью, как функцию n₂₁ показателя n₂ преломления водыотносительно показателя n₁ преломления воздухаи (рис. 10.2) φ угла ПП_л плоскости поляризации с ПП_д плоскостью падения этой световой волны:

ρ = I_┴′/I = {1 -[2/(1 + tg²υ₁)]}²sin²φ = {1 -[2/(1 + n₂₁)]}²sin²φ. (2.13)

Задача 10.3

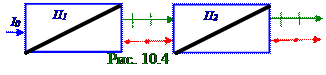
эта система пропускает в η раз больше света, чем при ориентированных под прямым углом друг к другу плоскостях пропускания этих П₁, П₂ поляризаторов. Найти P степень поляризации, которые создают два несовершенных П₁, П₂ поляризатора, когда их плоскости пропускания параллельны друг другу, и найти P₀ степень поляризации, которые создаёт каждый несовершенный

П₁, П₂ поляризатор в отдельности. Дано: η / P₀ = ? P = ?

Согласно (10.17) из раздела 10.1 "Электромагнитная природа света. Интерференция света" среднее (9.92) из раздела 9.0 " Электромагнитные волны. Излучение" значение модуля <S >плотности потокаэнергии или вектора SПойнтинга за Δt интервалвремени, которое называют Iинтенсивностью электромагнитнойи световойволны в произвольной точке пространства,пропорциональнаквадрату A²амплитуды световойволны. Усреднённый вектор< S >Пойнтинга (рис. 10.5, а), в направлении которого распространяется световаяэнергия, т.е. световойлуч, направлен по OY оси.

Естественный(рис. 10.1) из раздела 10.1 "Электромагнитная природа света. Интерференция света" неполяризованныйсвет с I₀ интенсивностью,имеющийв данный момент t времени направление вектора A амплитудысветовойволны согласно рис. 10.5, а), представляется суммой взаимно перпендикулярных поляризованных световых A_||,A _┴ векторов амплитуд, ориентированных соответственно по OZ, OX осям.

ИнтенсивностьI_||, I_┴ каждой из поляризованных световых лучей (рис. 10.5, б) равна половине I₀/2 интенсивности неполяризованногосвета. Поляризованные световые лучи с

I₀/2 интенсивностью(10.218) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом" получаются, если на вход идеального поляризатора направитьнеполяризованныйсвет с I₀ интенсивностью. Тогда на выходе идеального поляризатора(рис. 10.5, б), в)при ориентации его зеленой плоскости пропускания по OZ оси, будут поляризованные световые лучи с I_|| = I₀/2интенсивностью,световые A_||векторы амплитудкоторых ориентированы по OZ оси. При ориентации красной плоскости пропусканияпо OХ осина выходе идеального поляризатора(рис. 10.5, б), в) будут поляризованные световые лучи с I_┴ = I₀/2интенсивностью,световые A_┴ векторы амплитудкоторых ориентированы по OX оси.

На выходепервогоП₁ несовершенного поляризатора(рис. 10.5, б) световые лучи,световые A_┴ векторы амплитудкоторых ориентированы по OX оси, будут иметь α_┴I_┴ интенсивность,а световые лучи,световые A_||векторы амплитудкоторых ориентированы по OZ оси, будут иметь

α_||I_|| интенсивность, где α_┴, α_|| коэффициенты ослабления I_┴ = I₀/2, I_|| = I₀/2интенсивностейсветовых лучей в случае, если бы П₁ был идеальным поляризатором, ориентированным соответственнолибо по OX, либо по OZ оси.

На выходевторогоП₂ несовершенного поляризатора(рис. 10.5, б) в случае параллельности друг другу плоскостей пропускания несовершенных П₁, П₂ поляризаторов световые лучи,

A_┴ векторы амплитудкоторых ориентированы по OX оси, будут иметь α_┴²I_┴ интенсивность,а световые лучи,световые A_||векторы амплитудкоторых ориентированы по OZ оси, будут иметь

α_||²I_|| интенсивность.

На выходевторогоП₂ несовершенного поляризатора(рис. 10.5, б) в случае параллельности друг другу плоскостей пропускания несовершенных П₁, П₂ поляризаторов световые лучи будут (10.218) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом" частичнополяризованысоследующим с учётом рис. 10.2.1.5, б значением P степени поляризации:P = I_p/I_ч.п. = [α_|| ²I_|| - α_┴²I_┴]/[α_|| ²I_|| + α_┴²I_┴] = [α_|| ²(I₀/2) - α_┴²(I₀/2)]/[α_|| ²(I₀/2) + α_┴²(I₀/2)] =

= (α_|| ² - α_┴²)/(α_|| ² + α_┴²) ↔ α_|| = α_┴[(P + 1)/(1 - P)]^1/2, (3.1)

где I_p = α_|| ²I_|| - α_┴²I_┴ - (рис. 10.5, б)интенсивность поляризованных световых лучей на выходевторогоП₂ несовершенного поляризатора,полученная вычитанием из α_|| ²I_||интенсивности поляризованных световых лучей на выходевторогоП₂ несовершенного поляризатора,световые

A_||векторы амплитудкоторых ориентированы по OZ оси, α_┴²I_┴интенсивности поляризованных световых лучей на выходевторогоП₂ несовершенного поляризатора,световые A_┴ векторы амплитудкоторых ориентированы по OX оси; I_ч.п = α_|| ²I_|| + α_┴²I_┴ - (рис. 10.5, б)интенсивность частичнополяризованных световых лучей на выходевторогоП₂ несовершенного поляризатора в случае параллельности друг другу плоскостей пропускания несовершенных П₁, П₂ поляризаторов.

На выходевторогоП₂ несовершенного поляризатора(рис. 10.5, в) в случае ориентированных под прямым углом друг к другу плоскостях пропускания П₁, П₂ поляризаторов световые лучи, A_┴ векторы амплитудкоторых ориентированы по OX оси, будут иметь α_┴α_||I_┴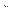

интенсивность,а световые лучи,световые A_||векторы амплитудкоторых ориентированы по OZ оси, будут иметь α_|| α_┴I_|| интенсивность. Это происходит потому, что световые лучи α_||I_|| интенсивности, световые A_||векторы амплитудкоторых ориентированы по OZ оси, с выходапервогоП₁ несовершенного поляризаторапопадаютна вход П₂ несовершенного поляризатора, красная плоскость пропусканиякоторого имеет α_┴ коэффициент ослабления,поэтомус выходаэтого П₂ несовершенного поляризатора интенсивностьсветового луча становится равной α_|| α_┴I_|| .Световые лучи α_┴I_┴ интенсивности, A_┴ векторы амплитудкоторых ориентированы по OX оси, с выходапервогоП₁ несовершенного поляризаторапопадаютна вход П₂ несовершенного поляризатора, зеленая плоскость пропускания которого имеет α_|| коэффициент ослабления,поэтомус выходаэтого П₂ несовершенного поляризатора интенсивностьсветового луча становится равной α_┴α_||I_┴.

Таким образом, с выходавторогоП₂ несовершенного поляризатора(рис. 10.5, в) в случае ориентированных под прямым углом друг к другу плоскостях пропускания П₁, П₂ поляризаторов световые лучи, A_┴ векторы амплитудкоторых ориентированы по OX оси, и световые лучи,световые A_||векторы амплитудкоторых ориентированы по OZ оси, будут иметь следующую одинаковую интенсивность: α_||α_┴I_|| = α_┴α_||I_┴ = α_┴α_||I₀/2, (3.2)

что является признаком того, что в этом случае с выходавторогоП₂ несовершенного поляризаторасветовые лучи являются неполяризованными.

С выходавторогоП₂ несовершенного поляризатора(рис. 10.5, в) в случае ориентированных под прямым углом друг к другу плоскостях пропускания П₁, П₂ поляризаторов I_ест интенсивность неполяризованныхили естественныхсветовых лучей имеет с учётом (3.2) следующий вид:

I_ест = α_||α_┴I_|| + α_┴α_||I_┴ = α_┴α_||I₀. (3.3)

Согласно условию, отношение I_ч.п = α_|| ²I_|| + α_┴²I_┴ (рис. 10.5, б)интенсивности частичнополяризованных световых лучей на выходевторогоП₂ несовершенного поляризатора в случае параллельности друг другу плоскостей пропускания несовершенных П₁, П₂ поляризаторов к

I_ест интенсивности неполяризованныхили естественныхсветовых лучей в случае ориентированных под прямым углом друг к другу плоскостях пропускания П₁, П₂ поляризаторов равно следующему значению:

I_ч.п /I_ест = (α_|| ²I_|| + α_┴²I_┴)/(α_||α_┴I_|| + α_┴α_||I_┴) = [α_|| ²(I₀/2) + α_┴²(I₀/2)]/α_┴α_||I₀ = (α_|| ² + α_┴²)/2α_┴α_|| = η.(3.4)

Подставляем (3.1) α_|| коэффициент ослабления в (3.4) и получаем следующее выражение

P степень поляризации, которые создают два несовершенных П₁, П₂ поляризатора, когда их плоскости пропускания параллельны друг другу: P = [1 - (1/η²)] ^1/2. (3.5)

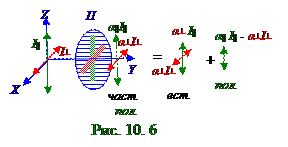
идеальным поляризатором, ориентированным соответственнолибо по OX, либо по OZ оси.

На выходеП несовершенного поляризатора(рис. 10.2.1.6) световые лучи будут (10.218) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом" частичнополяризованысоследующим с учётом рис. 10.6 значением P₀ степени поляризации:

P = I_p/I_ч.п. = [α_|| I_|| - α_┴I_┴]/[α_|| I_|| + α_┴I_┴] = [α_|| (I₀/2) - α_┴(I₀/2)]/[α_|| (I₀/2) + α_┴(I₀/2)] =

= (α_|| - α_┴)/(α_|| + α_┴) ↔ α_|| = α_┴(P + 1)/(1 - P), (3.6)

где I_p = α_|| I_|| - α_┴I_┴ - (рис. 10.6)интенсивность поляризованных световых лучей на выходе

П несовершенного поляризатора,полученная вычитанием из α_|| I_||интенсивности поляризованных световых лучей на выходеП несовершенного поляризатора,световые A_||векторы амплитудкоторых ориентированы по OZ оси, α_┴I_┴интенсивности поляризованных световых лучей на выходеП несовершенного поляризатора,световые A_┴ векторы амплитудкоторых ориентированы по OX оси; I_ч.п = α_|| I_|| + α_┴I_┴ - (рис. 10.6)интенсивность частичнополяризованных световых лучей на выходеП несовершенного поляризатора.

Подставляем (3.6) α_|| коэффициент ослабления в (3.4) и получаем следующее выражение

P₀ степени поляризации, который создаёт каждый несовершенныйП поляризатор:

P₀ = [(η -1)/(η + 1)] ^1/2. (3.7)

Задача 10.4

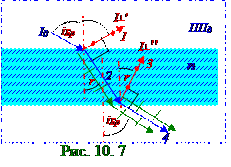
плоскопараллельной прозрачной пластине, 3 отражённого от нижней поверхности пластины и 4 прошедшего через толстую плоскопараллельную прозрачную пластину световых пучков.

Дано: i_Бр; ρ / P₁ = ? P₂ = ? P₃ = ? P₄ = ?

Согласно условию задачи υ₁ угол падения(рис. 10.7) световых лучей естественного

(рис. 10.1) из раздела 10.1 "Электромагнитная природа света. Интерференция света" или неполяризованногосвета с I₀ интенсивностью равен i_Бр углу Брюстера (10.219) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом", т.е. υ₁ = i_Бр, поэтому выполняется следующее соотношение: tgυ₁ = n , (4.1) где n - показательпреломления толстой плоскопараллельной прозрачной пластины относительно показателяпреломления вакуума, равного единице.

Согласнозакону Снеллиуса (9.104) из раздела 9.0 " Электромагнитные волны. Излучение"имеем следующее выражение, связывающее (рис. 10.7) υ₁ угол падения и υ₂ уголпреломления световых лучей: sinυ₁/sinυ₂ = n, (4.2) где υ₂ = r - угол (рис. 10.7) преломления световых лучей.

Совместное решение (4.1), (4.2) относительно υ₁ угла падения и υ₂ углапреломления световых лучейприводитк следующему выражению:

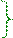
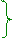tgυ₁ = n sinυ₁/cosυ₁= n ↔ cosυ₁ = sinυ₂ ↔ cosυ₁ = cos[(π/2) - υ₂] ↔

sinυ₁/sinυ₂ = n ↔ sinυ₁/sinυ₂ = n

↔ υ₁ = (π/2) - υ₂ ↔ υ₁ + υ₂ = π/2. (4.3)

Согласно (4.3) при (рис.10.7) падении световых лучей под i_Бр углом Брюстераотражённые1световые лучисI_┴′ интенсивностью, которые поляризованыв плоскости, перпендикулярной к поверхности ПП_д плоскости падения, перпендикулярны преломлённым

2световым лучам, которые частичнополяризованы в ПП_д плоскости падения.

Согласно формулам Френеляотношения I_┴′, I_||′ интенсивностей отражённых1 световых лучей от (рис. 10.7) поверхности толстой плоскопараллельной прозрачной пластины к

I_┴, I_|| интенсивностям падающих световых лучей на эту пластину, поляризованныхсоответственно перпендикулярно и параллельно ПП_д плоскости падениясветовых лучей, имеет следующий вид: I_┴′/I_┴ = sin²(υ₁ - υ₂)/sin²(υ₁ + υ₂); I_||′/I_|| = tg²(υ₁ - υ₂)/tg²(υ₁ + υ₂). (4.4) Согласно (4.4 ) отношение I_||′ интенсивности отражённых световых лучей от (рис. 10.7) поверхности толстой плоскопараллельной прозрачной пластины к I_|| интенсивности падающих световых лучей на эту пластину, поляризованных параллельно ПП_д плоскости падениясветовых лучей, равно нулю, т.к. при υ₁ + υ₂ = π/2 величина tg²(υ₁ + υ₂) → ∞. Поэтому (рис. 10.7) отражённые световые лучи,поляризованные параллельно ПП_д плоскости падениясветовых лучей, при падении световых лучей на поверхность толстой плоскопараллельной прозрачной пластины под i_Бр углом Брюстера, отсутствуют.

Степень поляризации P₁ отражённых от верхней поверхности пластины 1 световых лучей с учётом поляризованностис I_┴′ интенсивностьюэтих отражённых световых лучей толькоперпендикулярно ПП_д плоскости падения и с учётом отсутствия отражённых неполяризованныхили естественныхсветовых лучей с I_отр = 0 интенсивностью имеет следующий вид:

P₁ = I_┴′/(I_┴′ + I_отр) = 1. (4.5)Интенсивность I_┴′ отражённых световых лучей от (рис. 10.7) поверхности толстой плоскопараллельной прозрачной пластины, поляризованныхтолькоперпендикулярно

ПП_д плоскости падения, и с учётом отсутствия отражённыхнеполяризованныхили естественныхсветовых лучей с I_отр = 0 интенсивностью имеет следующий вид: I_┴′ = ρI₀, (4.6) где I₀ - интенсивность(рис. 10.7) падающих световых лучей на поверхность толстой плоскопараллельной прозрачной пластины под i_Бр углом Брюстера.

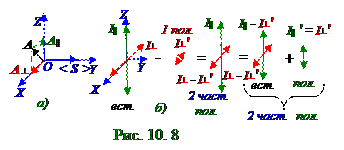
рис. 10.8, а, представляется суммой взаимно перпендикулярных поляризованных световых A_||,A _┴ векторов амплитуд, ориентированных соответственно по OZ, OX осям.

ИнтенсивностьI_||, I_┴ каждой из поляризованных световых лучей (рис. 10.8, б) равна половине I₀/2 интенсивности неполяризованногосвета.

Естественный плоский световой 1 пучок I₀ интенсивности, падающий в вакууме под i_Бр углом Брюстера на поверхность толстой плоскопараллельной прозрачной пластины, вследствие отражения световых лучей I_┴′ интенсивности, поляризованных(рис. 10.7) перпендикулярно

ПП_д плоскости падения, световые A_┴ векторы амплитуд(рис. 10.8, а) которых ориентированы по

OX оси, превращаются после (рис. 10.8, б) преломления в частичнополяризованный световой

2 пучок.

В этомчастичнополяризованном (рис. 10.8, б) световом 2 пучкеинтенсивность поляризованных световых лучей, световые A_┴ векторы амплитуд(рис. 10.8, а) которых ориентированы по OX оси, уменьшилась на величину I_┴′ интенсивности, отражённых от верхней поверхности пластины световых лучей, и стала равной I_┴ - I_┴′.

В частичнополяризованном (рис. 10.8, б) световом 2 пучкеинтенсивность поляризованных световых лучей,световые A_||векторы амплитуд(рис. 10.8, а) которых ориентированы по OZ оси, осталась равной I_||.

Частичнополяризованный (рис. 10.8, б) световой 2 пучок раскладывается на первую составляющую - неполяризованныеили естественныесветовые лучи со следующей с учётом (4.6) I_естинтенсивностью,являющейсясуммой I_|| - I_┴′ интенсивности,световые A_||векторы амплитудкоторых ориентированы по OZ оси, и I_┴ - I_┴′интенсивности,световые A_┴ векторы амплитудкоторых ориентированы по OX оси: I_ест = I_|| - I_┴′ + I_┴ - I_┴′ = I₀ - 2I_┴′ = I₀ - 2ρI₀, (4.7)

где I_|| = I₀/2, I_┴ = I₀/2 -интенсивностьI_||, I_┴ каждой из поляризованных световых лучей равна половине I₀/2 интенсивности неполяризованногосвета, падающего в вакууме под i_Бр углом Брюстера на поверхность толстой плоскопараллельной прозрачной пластины.

Второй составляющей частичнополяризованного (рис. 10.8, б) светового 2 пучка являютсяполяризованные с I_|| ′ = I_┴′ интенсивностьюлучи,световые A_||векторы амплитуд

(рис. 10.8, а) которых ориентированы по OZ оси.

Степень поляризации P₂ преломлённыхтолстой плоскопараллельной прозрачной пластиной падающего в вакууме под i_Бр углом Брюстера светового пучка I₀ интенсивности, в результате чегообразуетсячастичнополяризованный (рис. 10.8, б) световой 2 пучок с учётом (4.6), (4.7) имеет следующий вид: P₂ = I_┴′/(I_┴′ + I_ест) = ρI₀/ρI₀ + I₀ - 2ρI₀ = ρ/(1 - ρ). (4.8)

Согласно правилам геометрической оптики угол выхода (рис. 10.7)прошедшего через толстую плоскопараллельную прозрачную пластину 4 светового пучка равен их углу падения на эту пластину, т.е. i_Бр углу Брюстера.

Поэтому (рис. 10.7) отражённые3 световые лучиот нижней поверхности пластины с

.

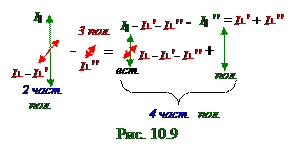
Интенсивность I_┴′′отражённых световых лучей от (рис. 10.7) нижней поверхности пластины 3 световых лучей, поляризованныхтолькоперпендикулярно ПП_д плоскости падения, с учётом (4.4) формул Френеляимеет следующий вид: I_┴′′ = ρ_┴( I_┴ - I_┴′), (4.10)

где ρ_┴ - коэффициент отражения поляризованных перпендикулярно ПП_д плоскости падениясветовых лучей; ( I_┴ - I_┴′) - интенсивностьпадающих световых лучей на нижнюю поверхность пластины 2 световых лучей, поляризованныхтолькоперпендикулярно ПП_д плоскости падения этих световых лучей.

Коэффициент (4.9) ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости падения световых лучейопределяется из следующего отношения интенсивности I_┴′ отражённых световых лучей от (рис. 10.7) поверхности толстой плоскопараллельной прозрачной пластины, поляризованныхтолькоперпендикулярно ПП_д плоскости падения, к (рис. 10.8, б) интенсивности I_┴ поляризованных перпендикулярно ПП_д плоскости падения поляризованных световых лучей, которые входят в общую (рис. 10.2.1.8, б) интенсивность неполяризованныхили естественныхсветовых лучей: ρ_┴ = I_┴′/ I_┴. (4.11) Подставляем (4.6) интенсивность I_┴′ отражённых световых лучей от (рис. 10.7) поверхности толстой плоскопараллельной прозрачной пластины, поляризованныхтолькоперпендикулярно ПП_д плоскости падения, и интенсивностьI_┴ поляризованных перпендикулярно ПП_д плоскости падения поляризованных световых лучей, равную половине I₀/2 интенсивности неполяризованногосвета, и получаем следующее выражение коэффициента ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости падения световых лучей: ρ_┴ = ρI₀/(I₀/2) = 2ρ, (4.12) где ρ - коэффициент отражения от пластины падающего светового потока, заданного в условии. Подставляем (4.12) коэффициент ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости падения световых лучей в (4.10) и получаем следующее выражениеI_┴′′ интенсивностиотражённых световых лучей от (рис. 10.7) нижней поверхности пластины 3 световых лучей: I_┴′′ = 2ρ( I_┴ - I_┴′). (4.13)Частичнополяризованный (рис. 10.9) световой 2 пучок I_|| + I_┴ - I_┴′ = I₀ - I_┴′ интенсивности, падающий (рис. 10.7) под r углом на от нижнюю поверхность толстой плоскопараллельной прозрачной пластины, вследствие отражения световых лучей

I_┴′′ интенсивности, поляризованных(рис. 10.7) перпендикулярноПП_д плоскости падения, световые A_┴ векторы амплитуд(рис. 10.8, а) которых ориентированы по OX оси, превращаются после преломления в частичнополяризованный световой 4 пучок.

В этомчастичнополяризованном (рис. 10.9) световом 4 пучкеинтенсивность поляризованных световых лучей, световые A_┴ векторы амплитуд(рис. 10.8, а) которых ориентированы по OX оси, уменьшилась на величину I_┴′′ интенсивности, отражённых от нижней поверхности толстой плоскопараллельной прозрачной пластины, и стала равной I_┴ - I_┴′- I_┴′′.

В частичнополяризованном (рис. 10.9) световом 4 пучкеинтенсивность поляризованных световых лучей,световые A_||векторы амплитуд(рис. 10.8, а) которых ориентированы по OZ оси, осталась равной I_||.

Частичнополяризованный (рис. 10. 9) световой 4 пучок раскладывается на первую составляющую - неполяризованныеили естественныесветовые лучи со следующей с учётом (4.5), (4.12) I_естинтенсивностью,являющейсясуммой I_|| - I_┴′- I_┴′′ интенсивности,световые A_||векторы амплитудкоторых ориентированы по OZ оси, и I_┴ - I_┴′- I_┴′′ интенсивности,световые A_┴ векторы амплитудкоторых ориентированы по OX оси:

I_ест = I_|| - I_┴′ - I_┴′′ + I_┴ - I_┴′ - I_┴′′ = I₀ - 2I_┴′ - 2I_┴′′ =

= I₀ - 2ρI₀ - 4ρ( I_┴ - I_┴′) = I₀ - 2ρI₀ - 4ρ[(I₀/2) - ρI₀) = I₀ - 4ρI₀(1 - ρ), (4.14)

где I_|| = I₀/2, I_┴ = I₀/2 -интенсивностьI_||, I_┴ каждой из поляризованных световых лучей равна половине I₀/2 интенсивности неполяризованногосвета, падающего в вакууме под i_Бр углом Брюстера на поверхность толстой плоскопараллельной прозрачной пластины.

Второй составляющей частичнополяризованного (рис. 10.9) светового 4 пучка являютсяполяризованные с I_||′′ = I_┴′ + I_┴′′ интенсивностьюлучи,световые A_||векторы амплитуд

(рис. 10.8, а) которых ориентированы по OZ оси.

Степень поляризации P₄ преломлённыхтолстой плоскопараллельной прозрачной пластиной падающего в вакууме под i_Бр углом Брюстера светового пучка I₀ интенсивности, в результате чегообразуетсячастичнополяризованный (рис. 10.2.1. 9) 4 световой пучок, прошедший через толстую плоскопараллельную прозрачную пластину, с учётом (4.5), (4.12), (4.13) имеет следующий вид: P₄ = (I_┴′+ I_┴′′)/( I_┴′+ I_┴′′+ I_ест) = ρI₀ + 2ρ[(I₀/2) - ρI₀)/{ ρI₀ + 2ρ[(I₀/2) - ρI₀)] + I₀ - 4ρI₀(1 - ρ)} =

= 2ρI₀ (1 - ρ)/ I₀(1 + 2ρ - 2ρ² - 4ρ + 4ρ²) = 2ρ(1 - ρ)/[1 - 2ρ(1 - ρ)]. (4.15) Согласно (4.15), (рис. 10.7) падающий в вакууме на поверхность толстой плоскопараллельной прозрачной пластины под i_Бр углом Брюстера световой пучокпосле его преломленияэтой пластиной превращается в частичнополяризованныйсветовой пучок.Световой пучок,полученный вследствие егопреломлениятолстой плоскопараллельной прозрачной пластиной,частичнополяризованв плоскости падения этого светового пучка.

Задача 10.5

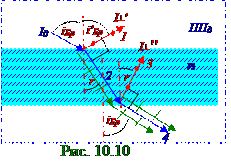
Подставляем (4.12) коэффициент ρ = ρ_┴/2отражения (рис. 10.10) от пластины падающего светового потока, выраженный через коэффициент ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости падения световых лучей, в (4.15) степень поляризации P₄ преломлённыхтолстой плоскопараллельной прозрачной пластиной светового 1 пучка, падающего в вакууме под i_Бр углом Брюстера, и получаем следующее выражение этой степени поляризации P₄ преломлённогосветового 1 пучка: P₄ = [1 - (1 - ρ_┴)²] /[1 + (1 - ρ_┴)²]. (5.1)

Согласно формулам Френеля(4.4) из "Задача 10.4" коэффициенты ρ_┴, ρ _|| отражения поляризованных перпендикулярно и параллельно ПП_д плоскости (рис. 10.10) падения световых лучей имеют следующий вид: ρ_┴ = sin²(υ₁ - υ₂)/sin²(υ₁ + υ₂); ρ _|| = tg²(υ₁ - υ₂)/tg²(υ₁ + υ₂). (5.2) Согласно правилам геометрической оптики угол выхода (рис. 10.10)прошедшего через толстую плоскопараллельную прозрачную пластину 4 светового пучка равен их углу падения на эту пластину, т.е. i_Бр углу Брюстера, поэтому в (5.2) угол υ₂ преломлениявышедшего из этой пластины4 светового пучка имеет следующий вид: υ₂ = i_Бр. (5.3)

Угол падения2 светового пучка на нижнюю поверхность толстой плоскопараллельной прозрачной пластины (рис. 10.10) равен r поэтому в (5.2) угол υ₁ паденияна нижнюю поверхность этой пластины 2светового пучка имеет следующий вид: υ₁ = r. (5.4) Отражённые3 световые лучи(рис. 10.10) от нижней поверхности пластины, которые поляризованыв плоскости, перпендикулярной к поверхности ПП_д плоскости падения, перпендикулярны преломлённым4 световым лучам, т.е. прошедшим через толстую плоскопараллельную прозрачную пластину, которые частичнополяризованы в ПП_д плоскости падения, поэтому (5.3), (5.4) связаны между собой следующим соотношением:

i_Бр + r = π/2 ↔ υ₁ = π/2 - υ₂. (5.5)

Подставляем (5.2) в формулы Френеляи получаем следующее выражение коэффициентов ρ_┴, ρ _|| отражения поляризованных перпендикулярно и параллельно ПП_д плоскости (рис. 10.10) падения световых лучей: ρ_┴ = sin²(π/2 - υ₂ - υ₂) = cos²2υ₂; ρ _|| = 0. (5.6)Использование тригонометрическихтождествприводит к следующему виду коэффициента

ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости (рис. 10.10) падения световых лучей: ρ_┴ = cos²2υ₂ = cos²υ₂ - sin²υ₂ = [1/(1 + tg²υ₂)] - [tg²υ₂/(1 + tg²υ₂)] =

= {[1/(1 + n²)] - [n²/(1 + n²)]} ² = (n² - 1)²/( n² + 1)², (5.7) где tgυ₂ = tg i_Бр = n - тангенс (рис. 10.10) углаБрюстера (10.219) из раздела 10.3 "Поляризация. Голография. Взаимодействие электромагнитных волн с веществом", равный n показателюпреломления толстой плоскопараллельной прозрачной пластины относительно показателяпреломления вакуума, равного единице.

Подставляем (5.7) коэффициент ρ_┴ отражения световых лучей, поляризованных перпендикулярно ПП_д их плоскости падения, в (5.1) и получаем следующее выражение степени поляризации P₄ преломлённыхтолстой плоскопараллельной прозрачной пластиной светового пучка, падающего в вакууме под i_Бр углом Брюстера, в зависимости от n показателяпреломления этой пластины относительно показателяпреломления вакуума, равного единице: P₄ = [( n² + 1)⁴ - (2n)⁴] /[( n² + 1)⁴ + (2n)⁴]. (5.8)

Задача 10.6

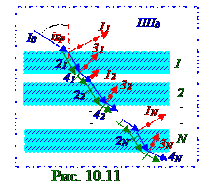
Частичнополяризованный (рис. 10.11) в ПП_д плоскости падения световой 4₁ пучок,преломлённый1 - ой толстой плоскопараллельной прозрачной пластиной, раскладывается на первую составляющую - неполяризованныеили естественныесветовые лучи со следующей с учётом (4.14) из "Задача 10.4"I_1естинтенсивностью: I_1ест = I₀ - 4ρI₀(1 - ρ), (6.1)

где I₀ -интенсивностьпадающих световых лучей на поверхность 1 - ой толстой плоскопараллельной прозрачной пластины под i_Бр углом Брюстера; ρ - коэффициентотражения от этой 1 - ой пластины падающего светового потока

Второй составляющей частичнополяризованного (рис. 10.11) светового 4₁ пучка,преломлённого1 - ой толстой плоскопараллельной прозрачной пластиной, являются(рис. 10.8, а) из "Задача 10.4" поляризованные со (4.15) из "Задача 10.4"следующей I_||′′ = I_1p интенсивностью светового пучка,световые A_||векторы амплитудкоторых ориентированы по OZ оси: I_1p = 2ρI₀ (1 - ρ). (6.2) Подставляем (4.12) из "Задача 10.4"коэффициент ρ = ρ_┴/2отражения (рис. 10.11) от пластины падающего светового потока, выраженный через коэффициент ρ_┴ отражения поляризованных перпендикулярно ПП_д плоскости падения световых лучей, в (6.1), (6.2) и получаем следующие выражения I_1ест, I_1pинтенсивностисоответственно естественнойи поляризованной составляющих светового 4₁ пучка,преломлённого1 - ой толстой плоскопараллельной прозрачной пластиной: I_1ест = I₀(1 - ρ_┴)²; I_1p = (I₀/2)[1 - (1 - ρ_┴)²] . (6.3)Частичнополяризованный (рис. 10.11) в ПП_д плоскости падения световой 4₁ пучок,преломлённый1 - ой толстой плоскопараллельной прозрачной пластиной, падает под i_Бр углом Брюстера на поверхность 2- ой, одинаковой с 1 - ой пластиной.

Поляризованная (рис. 10.11) в ПП_д плоскости падени