Дифракция световых волн: принцип Гюйгенса-Френеля 6 страница

Согласно (10.206) с увеличениемпорядка m - огодифракционного максимумаи количества Nщелейв ДРдифракционной решётке уменьшается минимальнаяδλразность двухдлин волн, которые по дифракционнойкартине воспринимаются по критериюРелеяраздельно.

Дифракция рентгеновских лучей на линейных цепочках структурных элементов. Формулы Лауэ

На кристаллах, у которых b расстояниемежду структурными элементами, т.е. атомами, ионами, порядка 10^{-10 м}, условия дифракциивыполняются для (10.7) из раздела 10.1 "Волновые свойства света" рентгеновских лучей с длинами волн10^{-14 м <} λ < 10^{-7 м}. Линейная (рис. 10.48)цепочка по OY оси структурных элементов, находящихся друг от друга на фиксированном h_y расстоянииили имеющих h_y период, при падении на неё параллельногопучка рентгеновских лучей под β₀углом, возбуждает согласно принципу Гюйгенса - Френеля

(рис. 10.15) из раздела 10.1 "Волновые свойства света" вторичную сферическую волновую поверхность рентгеновских лучей, которые распространяются в верхнюю полусферупод разными углами и в том числе под β углом к OY оси.

Оптическая(рис. 10.48) разность Δ_до хода лучей 1 и 2 в составе параллельногопучка рентгеновских лучейс плоским волновым фронтомв нижней полусфередо рассеяния на структурных элементахпо аналогии с оптической(рис. 10.37) Δ разностью ходамеждусоседними световымилучами на ДРдифракционной решёткеимеетследующую величину, равную катетув прямоугольномтреугольнике с h_y гипотенузойи β₀ углом между ними: Δ_до= h_ycosβ₀. (10.205)

При этом 2 луч отстаёт по фазе от 1 луча.

После рассеяния параллельные1′ и 2′ лучи, идущие под β углом к OY оси, имеют следующуюоптическую разность Δ_послехода, равнуюповеличине катетув прямоугольномтреугольнике с

h_y гипотенузойи β углом между ними: Δ_после = h_ycosβ. (10.206)

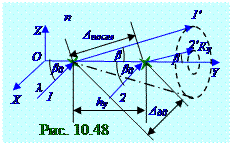
При этом 2′ луч опережает по фазе 1′ луч. Общая Δ₀оптическаяразность хода лучей 1′ и 2′, находящихся на К_yбоковойповерхности (рис. 10.37)конусас учётом Δ_дооптической разностей хода 1 и 2 лучейдо (10. 205) рассеяния и оптической Δ_после разностей хода 1′ и 2′ лучей после(10. 206) рассеяния, имеет следующий вид: Δ₀= Δ_после- Δ_до = h_y(cosβ - cosβ₀). (10.207) Если Δ₀общая (10.209) оптическая разность хода 1′ и 2′лучей,

находящихся на К_yбоковойповерхности (рис. 10.48)конуса, кратнаλ длине волны рентгеновских лучей, то на этой К_yбоковойповерхности конуса,будет наблюдаться их дифракционный максимум.

Таким образом, условием возникновения дифракционного максимума рентгеновских лучейс λ длиной волны на (рис. 10.48) К_yбоковойповерхности конуса являетсяследующее выражение: Δ₀= h_y(cosβ - cosβ₀) = ±m_yλ, (10.208)где m_y= ± 0, 1, 2, … - порядок дифракционного максимума на К_yбоковойповерхности конуса, ось которого направлена по OY оси координат, соответствующий линейной цепочке структурных элементовпо этой OY оси координат с h_y расстояниями между ними и дискретным значениям β₀, β углов соответственно падения и рассеяниярентгеновских лучей с λ длиной волны, распространяющихся в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ = λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на

рис.10.48. Знак "-" в номере m_y порядке дифракционного максимумасоответствует случаю, когда (cosβ - cosβ₀) разность в (10.208) отрицательна.

Линейные (рис. 10.49)цепочки по OX и OZ осям структурных элементов, находящихся друг от друга на фиксированныхсоответственно h_x и h_z расстояниях, при падении на них параллельныхпучков рентгеновских лучей с λ длиной волны под α₀и γ₀ углами образуют на К_x и К_zбоковыхповерхностях конусовc α и γ углами при вершине дифракционные максимумыпо аналогии с

(рис. 10.48) К_yбоковойповерхности конуса.

Таким образом, условием возникновения дифракционных максимумов рентгеновских лучейс λ длиной волны на К_x и К_zбоковых поверхностях конусов являютсяследующие выражения:

h_x(cosα - cosα₀) = ± m_xλ; h_z(cosγ - cosγ₀) = ± m_zλ.(10.209) где m_x; m_z = ± 0, 1, 2, … - порядки дифракционных максимумов на К_x и К_zбоковыхповерхностях конусов,оси которых направлены по соответственно осям OX и OZ осям координат; λ - длина волны рентгеновских лучей, распространяющихся в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ= λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.48.

Понятие о рентгеноструктурном анализе

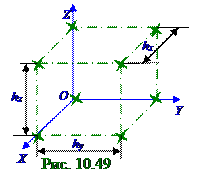
На поверхностях К_x,К_y и К_z конусовc α, β и γ углами при вершине (рис.10.49) рассеянныерентгеновские лучи с λдлиной волны образуют дифракционные максимумы на структурных элементах, которые представляют собой линейные цепочки по OX, OY и OZ осямс соответственно h_x, h_y и h_z периодами. Углы α, β и γ при вершине К_x,К_y и К_z боковыхповерхностях конусовсдифракционными максимумамирассчитываютсяпо формулам (10.208), (10.209) Лауэ при задании α₀, β₀и γ₀ углов падения параллельныхпучков рентгеновских лучей с λ длиной волны на структурные

элементы, которые представляют собой линейные цепочки по OX, OY и OZ осямс соответственно h_x, h_y и h_z периодами, и при задании m_x, m_y и m_z порядков дифракционных максимумов на этих К_x,К_y и К_z боковыхповерхностях конусов.

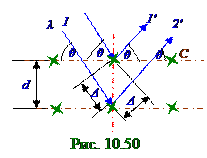
Рентгеновские лучи(рис. 10.50)с λ длиной волны движутся под θ углом скольженияк C поверхности кристалла, в котором для простоты атомныеплоскости, т.е. плоскости, проведённые через узлы кристаллической решётки, совпадают и параллельныэтой Cповерхности кристалла. Расстояние между соседними атомнымиплоскостями равно d. Рентгеновские2 лучи(рис. 10.50)с λ длиной волны падают

Дифракция рентгеновских лучей на совершенном кристалле, условие Брэгга – Вульфа

под θ углом скольженияот узла кристаллической решётки, который находится на C поверхности кристалла, и отражаетсяот него под тем же θ углом скольжения.Рентгеновские1 лучипадают на узел кристаллической решётки, находящегося на второй атомнойплоскости, и отражаютсяот него под тем же, что ирентгеновские2 лучиθуглом скольжения.

Оптическаяразность хода между отражёнными1' - ым и 2' - ым рентгеновскимилучамиравняется следующим двум2Δ катетам в прямоугольном треугольнике с гипотенузой, равной

d расстоянию между соседними атомными плоскостями: 2Δ = 2dsinθ. (10.210) Если оптическаяразность хода в (10.210) между отражёнными1' - ым и 2' - ым рентгеновскимилучами кратнацелому числу λ длин волн, то по аналогии с дифракционными максимумами (10.163) у световых волн в направлении θ угла скольженияэтих отражённых рентгеновскихлучейвозникает дифракционный максимум. С учётом (10.210) условие

Брэгга - Вульфасуществованиядифракционных максимумову отражённых рентгеновских лучей, имеющих λ длину волны, в направлении θ угла скольженияотатомныхплоскостей с d расстоянием между ними имеет следующий вид: 2dsinθ = mλ. (10.211)

где m - целоечисло, принимающее значения 1, 2, 3, …, называемое порядком отражения.

Дата добавления: 2016-02-14; просмотров: 759;