Дифракция на пространственной решетке. Дифракция рентгеновских лучей и рентгеноструктурный анализ

В – Бр. предложен простой метод расчета дифр. рентгеновского излучения от кристаллической решетки. Они предполож., что дифр. р. и. явл. результатом их отражения от системы параллельных кристаллографических плоскостей.

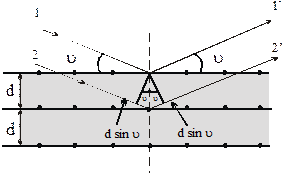
u- угол скольжения

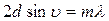
(m=1,2,3,..)

т.е. при разности хода между двумя лучами, отраженными от соседних кристаллограф. плоскостей, кратной целому длин волн, наблюдается дифр. max .

Формула Вульфа-Брэггов используется при решении двух важных проблем :

1.Определение структуры вещества ( рентгеноструктурный анализ ):

наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измерении u и m, можно найти межплоскостное расстояние (d) .

2. Определение длины волны падающего рентгеновского излучения (рентгеновская спектроскопия):

наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известном d и измеряя u и m можно найти длину волны падающего рентгеновского излучения.

Закон Бугера и связь его с дисперсией света.

Опр.1 Поглощением ( адсорбцией ) света называется явление потери энергии световой волны , проходящей через вещество , вследствия преобразования энергии волны в другие формы ( например , во внутреннюю энергию вещества).

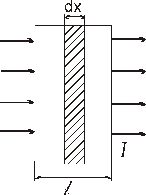
Пусть на прозрачную пластинку толщиной λ падает монохроматического света , интенсивностью 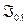.После прохожд. света через пластинку , его интесивность .

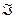Бугер предположил , что в 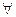сечении пластинки справедливо соотношение :

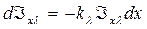
Где d_x - элемент пластинки , толщиной x, k_λ - коэффициент поглощения среды.

При увеличении х (dx>0), 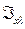уменьшается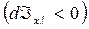

интегрируя получаем :

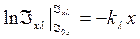
Отсюда :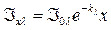

При х=е, получаем :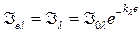

- это выражает закон Бугера , установленный в 1729 г.

Иногда его записывают в таком виде

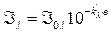
где 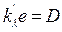– называется оптической плотностью вещества, 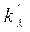– коэффициент поглощения.

Опр.2 Величина 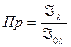называется прозрачностью вещества.

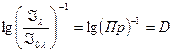
Логарифм величины , обратной прозрачности равен оптической плотности вещества , т. е. чем вещество более оптически плотно , тем меньше его прозрачность.

Беером установлено , что для ряда растворов

,

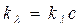где 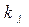- новый коэффициент поглощения , с – концентрация вещества.

Подставляя в закон Бугера 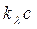получим закон Бугера – Беера

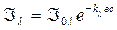
Отсюда концентрация вещества ( раствора ):

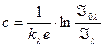
Поскольку 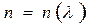, то и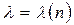

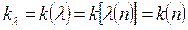
т.е. коэфф. поглощения зависит от показателя преломления. В этом и заключается прямая связь между поглощением и дисперсией света.

§1. Дисперсия света и способы ее наблюдения.

Спектры призматический и дифракционный.

Опр1. Дисперсией света называется зависимость показателя преломления n вещества от частоты ( длины волны ) света или зависимость фазовой скорости u световых волн от его частоты ν

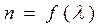
При пропускании пучка естественного света через трехгранную призму, изготовленную из какой-либо прозрачной среды, на экране Э появятся цветные полоски, начиная с красной и кончая фиолетовой

К, О, Ж, З, Г, С, Ф

Если на месте цветной полоски поместить грань второй трехгранной призмы , как указано на рис., то повторное преломление света, обладающего различными длинами волн, даст цветную кривую на экране, поставленно за второй призмой, которую называют дисперсионной кривой. Такое полож. призм назыв. скрещенным.

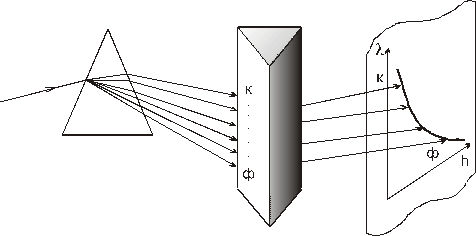
Зависимость показателя преломления n среды от частоты ν ( длины волны ) нелинейная и немонотонная.

Опр 2. Области значений ν(λ) в которых 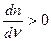, , 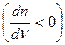т. е. с ростом ν увеличевается так же и n соотв. нормальной дисперсии света.

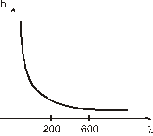
Например, обычное стекло , прозрачно для видимого света и в этой области частот набл. норм. дисперсия.

Опр 3. Дисперсия света называется аномальной если 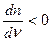, т. е. с ростом ν показатель преломления среды уменьшается.

Аном. дисперсия наблюдается в областях частот, соответству-ющих полосами интенсивного поглощения света в данной среде, например, у обычного стекла эти полосы находятся в инфрокрасной и ультрафиолетовой частях спектрах.

Рассмотрим различия в дифракционном и призматическом спектрах.

1. Дифр. реш. разлогает падающий свет непосредственно по длинам волн , поэтому по измеренным углам (по направлениям соответст-вующих max ) можно вычислить длину волны.

Разложение света в спектр в призме происходит по значениям показателя преломления , поэтому для опред. λ необходимо знать зависимость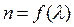

2. Составные цвета в дифр. и призм. спектрах располагаются различно. В дифр. решетке , 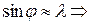, т. к. 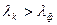, то красные лучи отклон. дифр. решетки сильнее.

Призма же разлагает лучи в спектр по значениям показателя преломления , для всех прозрачн. веществ с ув.длины волны монотонно уменьшается 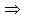, т. к. 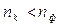, то красные лучи отклоняются слабее.

Получение и анализ поляризованного света.

Закон Мамоса.

Поляризованный свет можно получить, по крайней мере тремя различными способами :

а) при прохождении световых лучей через оптически активные среды , б) при отражении и преломлении световых волн , в) при рассеяние световых лучей.

Рассмотрим каждый из этих способов :

а) Кристаллические пластинки турмалина и исландского шпата пропускают свет только с одним преимущественным направлением колебания вектора 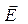. Это направление 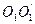называется оптической осью.

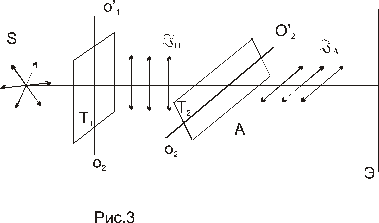
Рассмотрим классич. опыты с турмалином. Напрвим естеств. свет порпендикулярно пластинке турмалина Т₁ ( поляризатор ). Вращая кристалл Т₁ вокруг направления луча, то никаких изменений не наблюдается. Если на пути луча поставить вторую пластинку турмалина Т₂ и вращать ее вокруг направл. луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от угла α между оптич. осями кристаллов по закону Малюса :

,

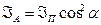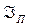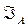где и - соответственно интенсивность света падающего на второй кристалл и вышедшего из него.

Св-во 1: Интенсивность света прошедшего через пластинки изменяется от min ( полное гашение света ) при 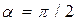(оптические оси пластинок пепендик.) до max 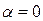( оптич. оси )

Док-во:

з-на Малюса

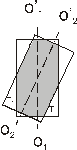
Амплитуда 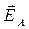светов. колебаний , прошед-ших через пластинку Т₂ будет меньше ампли-туды световых колебаний 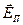, падающих на Т₂ :

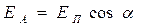
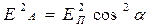
Þ (учитывая , что 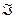пропорционально Е²) получим закон Малюса

Св-во 2: Из поляризатора выходит плоско поляризованный свет интенсивность которого

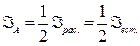
Опр. 1: Степенью поляризации называется величина

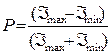
где 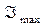и 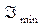- max и min интенсивности света, соотв. двум взаимно компонентам вектора 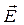. Для естеств. света ; P=0 ; для плоскополяризов. и Р=1.

б) Поляризация света при отражении и преломление на границе двух диэлектриков.

( Например , воздух и стекло ).

Закон Брюстера : При угле падения 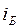( угол Брюстера ) определяемого соотношением

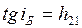
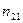( - относительный показатель преломления ) отраженный луч является плоскополяризованным.

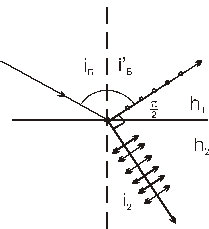
Преломленный же луч при угле 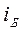поляризуется max но не полностью.

Св-во 1: Если свет падает под 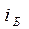но отраженный и преломленный лучи взаимно перпендикулярны.

;

.

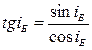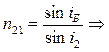
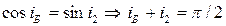но 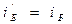закон отражения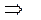

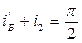
Св-во 2 Степень поляризации преломления света может быть значительно повышена за счет многократного преломления , при условии падения на границу раздела под углом .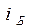

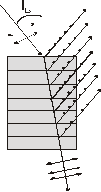
Например , для стекла n=1,2,3 степень поляриз. прим. 15 , после преломления на 8-10 пластинок луч полностью поляризован.

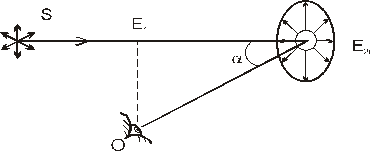
в) Поляризация при рассеянии света на оптических неоднородностях.

( Рассеяние солнечного света воздухом ).

Если угол зрения будет составлять с направлением луча в угол 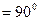, то рассеянный в направл. наблюдателя свет, будет полностью поляризован.

при α₂ < α₁ ; P₂ < P₁

§ 3.Одноосные и двуосные кристаллы.

Двойные лучепреломления.

Опр. 1 Среда наз. оптически изотропной , если ее оптические св-ва по всем направлениям среды одинаковы.

Рассмотрим анизотропные среды , оптич. св-ва которых зависят от изменения направления. Анизотропн. среды проявл. в различн. поведении диэлектрич. проницаемости ε по мере изменения выбираемого направления в среде.

Введем внутри кристалла дек. сист. коорд. XYZ. По осям отложим отрезки 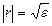, равные 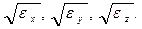Опишем радиус- вектором 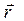поверхность, называемую пов-тью оптической индикатрисы среды.

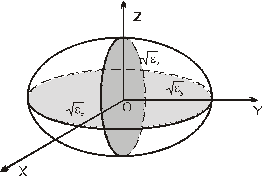
Уравнение этой пов-ти :

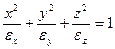
- ур-ние эллипсоиды. Оси симметрии элл. оред. три главных направления среды , которым соотв. три главн. значения диэл. проницаемости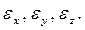

Св-во 1: if 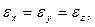то элл. превращается в сферу . В этом случае среда будет оптически изотропной.

2: if 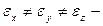двуосный кристалл (сера , гипс , смола ).

3: if 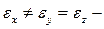кристалл одноосный , а оптическая индикатриса явл. эллипсоидом вращения. Ось ОХ – оптическая ось кристалла.

В общем случае вектор электрического смещения 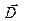не всегда совпадает с вектором 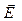однако , имеет место соотношение :

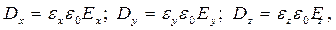
Св-во 4: if 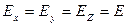т. е. в случае изотропной среды вектора совпадают по направлению.

Св-во 5: Если вектор 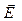направлен хотя бы по одному из анизотропных направлений ОХ, ОY и OZ, то векторы 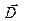и 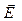совпадают

Док-во: Пусть 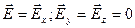, тогда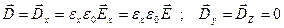

Опр. 2 Все прозрачные кристаллы ( кроме кристаллов кубической системы , являющихся оптически изотропными ) обладают способностью раздваивания каждого падающего на них светового пучка называемую способностью двойного лучепреломления.

Эта особенность преломления лучей была обнаружена и описана в 1670г. Э.Бартолином ( 1625-1698 ) для исландского шпата (разновидность кальцита CaCO₃).

Если на кристалле исландского шпате направить узкий пучок света , то из кристалла выходят два луча , параллельных друг другу и падающему лучу , причем в одноосном кристалле один из лучей подчиняется законам преломления света ,

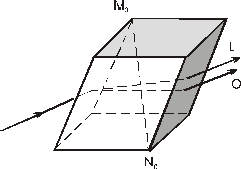
поэтому назван обыкновенным лучем (о) , второй луч (е) назван необыкновенным , т. е. не удовл. законам преломления.

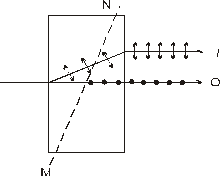
При нормальном падении света на пов-ть пластинки, вырезанный из одноосного кристалла, необыкн. луч преломляется.

Анализ поляризации света показыв., что (е) и (о) поляризов. в 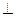плоскостях.

Опр. 3 Главной плоскостью ( или главным сечением кристалла ) называется плоскость, проходящая через направление луча света и оптическую ось кристалла.

Т. е. плоскость колеб. (о) 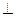пл-ти главного сечения , а пл-ть колеб. необыкнов. (е) находится в плоскости глав. сеч.

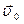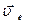Обозначим и скорости обыкн. и необыкнов. лучей соответственно 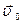численно одинакова по всем направл.:

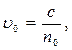
где 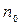-показат. преломл. кристалла для обыкнов. луча . Соответственно для необык.

,

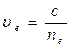где 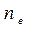-пок. пр. для необыкн. луча. Значение 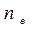и 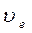зависят от направления необыкнов. луча по отнош. к оптич. оси кристалла.

Для лучей распростр. вдоль оптич. оси ; 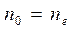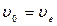, т. е. только одна скорость рапростр. света.

Пусть S-источник света , находящийся внутри одноосного кристалла OO' - направл. оптич. оси. Волновой пов-тью распростран. (о) явл. сфера ( 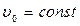) , необыкнов. (е) ( 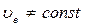) – эллипсоид вращения.

Опр. 4 Если 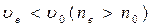, то одноосный кристалл назыв. положительным (кварц и др.).

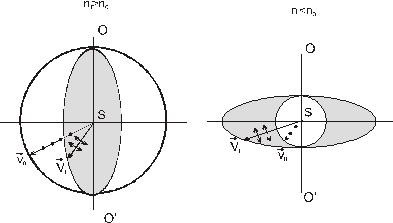
Опр. 5 Если 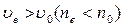, то одноосный кристалл назыв. отрицательным (исландский шпат и др.).

Пов-ти скоросте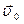й и 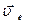теснейшим образом связаны с оптическими. В системе Гауса:

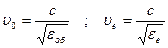
§ 4. Поляризующие пластики, поляройды, призмы и их практическое применение.

В основе поляризационных приспособлений, служащих для получения поляриз. света, лежит явление двойного лучепреломления. Наиболее часто для этого применяют призмы и поляройды.

Призмы делятся на два класса:

1.)Призмы, дающие только плоскополяризованный луч (поляризационные призмы)

2.)Призмы, дающие два поляриз. во взаимно ┴ плоскостях луча (двоякопреломляющие призмы)

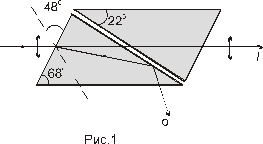
Призма Николя (двойная призма из исландского шпата, склеенная вдоль оси АВ канадским бальзамом), с_n=1,55 (n₀=1,66 , n_e=1,51)

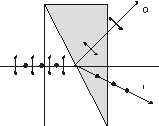
Двоякопреломляющие призмы (исландский шпат и стекло, или обе из исландского шпата со взаимно ┴ оптич. осями.

Опр. 1 Различное поглощение света в зависимости от ориентации вектора 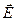называется дихроизмом, а двоякопреломляющие кристаллы, обладающие этим св-вом назыв дихроичными кристаллами.

§ 5. Интерференция поляризованных лучей.

На кристаллич. пластинку, вырезанную ║ оптич. оси пормально падает плоскополяризованный свет. Он разделяется на (о) и (е), которые в кристалле пространственно не разделимы, но движ. с разными скоростями, а на выходе из кристалла складываются.

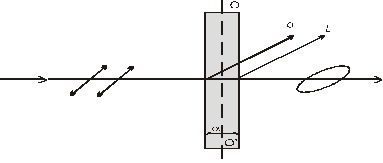
Т.к. (о) и (е) колебания светового вектора совершаются во взаимно ┴ плоскостях, то на выходе из пластинки в результате интерференции возникают световые волны, вектор 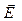в которых изменяется так, что его конец описыв. эллипс, ориентиров. произвольно относительно координатных осей.

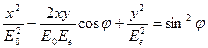
Е₀ , Е_е –соотв. напряж. эл. поля волны в (о) и (е)

φ – разность фаз колебаний