Принцип Гюйгенса-Френеля. Интеграл Френеля и дифракция света. Метод зон Френеля.

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Для наблюдения дифракции световых волн необходимо создание специальных условий. Это обусловлено тем, что масштабы дифракции сильно зависят от соотношения размеров препятствия и длины волны. При длине волны, сравнимой с размерами препятствия (что обычно имеет место для звуковых волн), дифракция выражена очень сильно. В случае если, как это имеет место для света, длина волны значительно меньше размеров препятствия дифракция выражена слабо и обнаруживается с трудом.

Явление дифракции волн может быть объяснено с помощью, принципа Гюйгенса (см. т. I, &83). Однако принцип Гюйгенса не даёт никаких об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранён Френелем, который дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Учёт амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. С помощью усовершенствованного им принципа Френелю удалось дать удовлетворительное объяснение ряда дифракционных явлений, а так же устранить одно из основных затруднений волновой теории света - показать, как согласуется волновая природа с наблюдающимся на опыте прямолинейным распространением света.

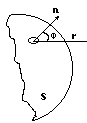Пусть S на (рис.1) представляет собой одну из волновых поверхностей света, распространяющегося от некоторого источника. Амплитуда светового колебания в точке P, лежащей перед этой поверхностью, может быть согласно Френелю найдена из следующих соображений. Каждый элемент поверхности служит источником вторичной сферической волны, амплитуда которой пропорциональна величине

элемента dS. Амплитуда сферической волны убывает, с расстоянием r рис.1от источника по закону 1/r [см. т. I, формулу(78.9)].

Следовательно, от каждого участка dS волновой поверхности в точку P приходит колебание

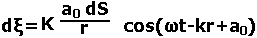(1.1)

В этом выражении (ωt+a₀)-фаза колебания в месте расположения волновой поверхности S, k-волновое число, r-расстояние от элемента поверхности dS до точки P. Величина а₀определяется амплитудой светового колебания в том месте, где находится dS. Коэффициент пропорциональности kФренель считал убывающим при увеличении угла φ между нормалью n к dS и направлением от dSк точке P и обращающимся в нуль при φ=π/2.

Результирующее колебание в точке P представляет собой суперпозицию колебаний (1.1), взятых для всей волновой поверхности S:

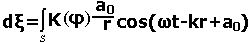(1.2)

Формулу (1.2) можно рассматривать как аналитическое выражение принципа Гюйгенса - Френеля.

Вычисления по формуле (1.2) представляют собой в общем случае чрезвычайно трудно задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть может быть осуществлено простым алгебраическим или геометрическим суммированием.

Различают два случая дифракции. Если источник света и точка наблюдения P, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или о дифракции в параллельных лучах.

Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис.2)

рис.2

Применим принцип Гюйгенса - Френеля для нахождения амплитуды светового колебания, возбуждаемого в точке P сферической волной, распространяющегося в однородной среде из точечного источника S (рис 3). Волновая поверхность такой волны симметрична относительно прямой SP. Воспользовавшись этим, Френель разбил волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки P отличаются на λ/2 (λ-длина волны в той среде, в которой распространяется волна). Легко видеть, что расстояние b_m от внешнего края m-й зоны до точкиPможно представить следующим образом:

b_m=b+mλ/2 (2.1)

где b-расстояние от вершины волновой поверхности O до точки P.

рис.3

Колебания, проходящие в точку P от аналогичных точек двух соседних зон (т.е., от точек, лежащих у внешних краёв зон, или в середине зон и т.д.), будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на π.

Для оценки амплитуд колебаний нужно найти площади зон. Внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент (рис.4).

рис.4

Обозначим площадь этого сегмента S_m. Тогда площадь m-й зоны можно представить в виде:

ΔS_m=S_m--S_m-1

Где S_m-1-площадь сферического сегмента, выделяемого внешней границей (m-1)-й зоны.

Из (рис. 4) следует, что

r²_m=a²-(a-h_m)²=(b+mλ/2)²-(b+h_m)²

(a-радиусволновой поверхности, r_m радиус внешней границы m-й зоны ).

Возведя скобки в квадрат, получим

r²_m=2ah_m-h_m²=bmλ+m²(λ/2)²-2bh_m-h_m² (2.2)

откуда

(2.3)

Ограничиваясь рассмотрением не слишком больших m, можно ввиду малости λ пренебречь слагаемым, содержащим λ². В этом приближении

(2.4)

Площадь сферического сегмента равна S=2πR/h(R-радиус сферы, h-высота сегмента). Следовательно,

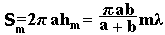
а площадь m-й зоны Френеля

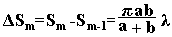
Полученное нами выражение не зависит от m. Это означает, что при не слишком больших m площади зон Френеля примерно одинаковы.

Произведём оценку радиусов зон. Согласно (2.2) r²_m=2ah_m-h²_m. При не слишком больших m высота сегмента h_m<<a, поэтому можно считать, что r²_m=2ah_m. Подставив сюда значение (2.4)для h_m найдём радиус внешней границы m-й зоны Френеля .

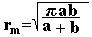(2.5)

Если положить a=b=1м, то для радиуса первой центральной зоны получается значение:r₁=0,5 мм. Радиусы последующих зон возрастают как .

Выше мы нашли, что площади зон Френеля примерно одинаковы. Расстояние b_m от зоны до точки P медленно растёт с m по линейному закону см(2.1).Угол φмежду нормалью к элементам зоны и направлением на точку P также растёт с номером зоныm. Всё это приводит к тому, что амплитуда A_m колебания, возбуждаемого m-й зоной в точке P, монотонно убывает с ростом m см(1.1). Даже при очень больших m, тогда, как можно заключить из (2.3), площадь зоны начинает заметно расти с m, убывание множителя K(φ) превышает рост ΔS_m и стремится к нулю при φ->π/2, так что A_m продолжает убывать. Таким образом, амплитуда колебаний, возбуждаемых в точке P зонами Френеля, образуют монотонно убывающую последовательность:

А₁>А₂>А₃>…>А_m-1>А_m>А_m+1>…

Фазы колебаний, возбуждаемых соседними зонами, отличаются на π. Поэтому амплитуда А результирующего светового колебания в точке P может быть найдена, алгебраически:

А=А₁-А₂+А₃-А₄+… (2.6)

В это выражение все амплитуды от нечётных зон входят с одним знаком, а от чётных зон-с другим знаком. Запишем (2.6)в виде:

А=А₁/2+(А₁/2-А₂+А₃/2)+(А₃/2-А₄+А₅/2)+… (2.7)

Вследствие монотонного убывания А_m можно приближённо считать, что

А_m=(А_m-1+ А_m+1)/2

При этом условии выражения, заключённые в круглые скобки, будут равны нулю и формула(2.7) упрощается следующим образом:

А=А₁/2 (2.8)

Полученный нами результат означает, что амплитуда создаваемая в некоторой точке P сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной. Иными словами, действие, всей волновой поверхности эквивалентно половине действия всей центральной зоны. По произведённой выше оценке центральная зона имеет размеры порядка долей миллиметра. Следовательно, свет от точки S к точке P распространяется как бы в пределах очень узкого прямого канала, т.е. практически прямолинейно.

рис.5

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля ,амплитуда в точке P будет равна А₁ т.е. в два раза превзойдёт амплитуду (2.8). Соответственно, интенсивность света в точке P будет в этом случае в четыре раза больше, чем при отсутствии преград между точками S и P.

Колебания от чётных нечётных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все чётные или все нечётные зоны, то амплитуда колебания в точке P резко возрастает. Такая пластинка называется зонной. На (рис.7) изображена зонная пластинка, перекрывающая чётные зоны.

Зонная пластинка во много раз увеличивает интенсивность света точке P, действуя подобно собирательной линзе. Ещё большего эффекта можно достигнуть, не перекрывая чётные или нечётные зоны, а изменяя фазу их колебаний на π. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих чётным и нечётным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой.

рис.7

По сравнению с обычной (или амплитудной) зонной пластинкой фазовая даёт дополнительное увеличение амплитуды в два раза, а интенсивности света в четыре раза.