Амплитуда колебаний в точке наблюдения

Пусть первая зона (совокупным действием всех своих малых элементов dS) вызовет в точке Р колебания амплитуды А₁, вторая зона – колебания амплитудой А₂, …, т-я зона – колебания амплитудой А_т.

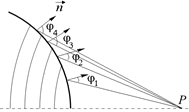Рис. 20.13

Площади зон примерно одинаковы, но угол j между нормалью к волновой поверхности и направлением на точку Р от зоны к зоне постепенно растет (рис. 20.13). А значит, коэффициент K(j) в формуле (20.1) от зоны к зоне монотонно убывает! Поэтому и амплитуды А₁, А₂, А₃, …, А_т монотонно убывают:

А₁ > А₂ > А₃ > … > А_т > A_m+1 > …

Допустим, что величины А₁, А₂, А₃, …, А_т нам известны. Попробуем определить амплитуду результирующего колебания в точке Р. Поскольку можно сказать, что колебания, возбужденные соседними зонами, находятся в противофазе (т.е. отличаются по фазе на p), результирующая амплитуда в точке Р может быть представлена в виде

А = А₁ – А₂ + А₃ – А₄ + … (20.7)

В этом выражении амплитуды от нечетных зон входят со знаком плюс, а от четных – со знаком минус. Сделаем такое «хитрое» преобразование равенства (20.7):

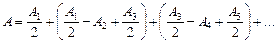(20.8)

Поскольку последовательность {A_m} монотонно (и достаточно медленно) убывает, можно приближенно считать

.

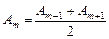Тогда все выражения в скобках обратятся в нуль, и мы получим результат

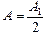, (20.9)

т.е. амплитуда колебания, создаваемого в точке Р всей сферической волной, равна только половине амплитуды колебания, создаваемого в этой точке одной первой зоной Френеля! Согласитесь, удивительный результат!