Амплитуданы график арқылы анықтау

Дифракциялық құбылыстарды талдаудың графиктік амалы “Френель спиралы” деп аталатынды қолдануға негізделген.

Гюйгенс-Френель интегралымен бейнеленетін қорытқы жарық өрісін есептеу элементарлық екінші реттік көздері қоздыратын жарық тербелістерін қосуға саяды. Есеп математикалық тұрғыдан жиіліктері бірдей, бірақ амплитудалары мен фазалары әртүрлі гармоникалық тербелістерді қосуға келтіріледі. Осы есепті шешудің көрнекі амалы – векторлық диаграмманы тұрғызу.

Жиілігі w амплитудалары мен фазалары кез-келген болатын бірнеше гармоникалық тербелістердің қосындысы да жиілігі w гармоникалық тербеліс болады. Қорытқы тербелістің нақты А амплитудасын және j фазасын векторларды қосу ережесі бойынша тербелістерді-қосындыларды кескіндейтін векторларды қосып табуға болады. Әрбір осындай вектордың ұзындығы тербеліс амплитудасына тең, және абсцисса осіне көлбеу бұрышы берілген тербелістің фазасына тең болады. Векторлық қосындыны тұрғызғаннан кейін қорытқы тербеліс амплитудасы алынған қосынды - вектордың ұзындығы ретінде, ал қорытқы тербеліс фазасы – осы вектордың абсцисса осіне көлбеу бұрышы ретінде табылады.

Векторлық диаграмманың тұрғызылуы 3-суретте келтірілген.

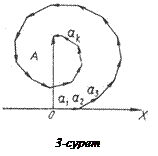Ол былай тұрғызылады. Френель аумағын көптеген концентрлік сақиналарға (аумақшаларға) бөлеміз. Сірә, бөлуді аумақшалардың аудандары шамамен бірдей болатындай, ал аумақшалар саны жеткілікті үлкен болатындай етіп іске асыруға болады. Осы жағдайда аумақшалардың үлестері ұзындықтары бірдей, бірақ абсцисса осіне көлбеулік бұрыштары әртүрлі векторлармен кескінделеді. Бірінші және соңғы векторлар, Френель аумағының анықтамасына сәйкес, бір-біріне қатысты p бұрышқа бұрылған. Радиус өскен сайын аумақша үлесі (демек, тиісті вектор ұзындығы), 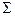бетіне нормаль мен бақылау нүктесіне бағыт арасындағы бұрыштың өсуі себепті, аздап кемиді.

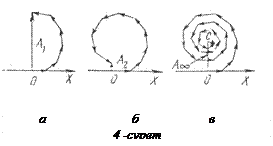Осы сияқты Френельдің бірінші аумағының, (4 а-сурет), және де нөлінші және бірінші аумақтарының бірігіп (4б-сурет) дифракциялық интегралға үлесін кескіндейтін вектор тұрғызылады. Аумақтың нөмірі өсуімен оның аумақшаларын кескіндейтін элементар векторлар қысқара түседі. Бұл қосынды дифракциялық өріске берілген аумақтың жалпы үлесінің осы аумақтың көлбеулік бұрышының өсуімен, яғни К(j) факторымен байланысты кемуін көрсетеді.

Аумақ санын барған сайын өсіріп векторлық диаграмманы тұрғызу амалын жалғастырғанда бұралған спираль аламыз (4в-сурет). Әрбір аумақтың аумақша санын өсіргенде векторлық диаграмманың сынық сызықтары барған сайын тегіс қисыққа жақындай түсетіндігін көруге болады. Френель аумақтарының бәрі ашылған және әрбір аумақтың аумақшалар саны шексіздікке ұмтылатын шектік жағдайда 5–суретте көрсетілген векторлық диаграмма алынады. Осы шектік диаграмма бұралған тегіс спираль-Френель спиралі түрінде болады.

Жарық толқынының 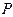нүктесіндегі қорытқы әрекетін қайсыбір фазалар айырымға ие тербелістерді графиктік қосу әдісі көмегімен қарастыру ыңғайлы. Осы әдіс көп жарық шоқтарының интерференциясын қарастырғанда да қолданылады.

Тербелістерді графиктік қосу үшін 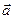векторы амплитуда векторы жайындағы ұғымды пайдаланамыз. 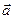векторы амплитуда векторы болса, онда оның ұзындығы тербеліс амплитудасына тең болады, ал осы вектордың берілген ОХ бағытымен жасайтын a бұрышы қарастырылып отырған тербелістің бастапқы фазасына сәйкес келеді. 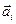векторлары арқылы кескінделетін бірнеше тербелмелі қозғалыс қосылған кезде қосынды тербеліс 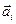векторларының векторлық қосындысына тең 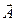векторымен кескінделеді.

Толқындық шеп бетін аудандары бойынша теңдей, Френель аумақтарына ұқсас, бірақ әлдеқайда жіңішке сақиналық аумақшаларға бөлеміз. 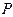нүктесіне осындай бірінші аумақшадан келетін тербеліс 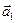векторымен кескінделеді. Осы тербелістің бастапқы фазасы нөлге тең деп ұйғарамыз. Сонда 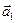векторы ОХ осі бойында жататын болады (3-сурет). Көрші аумақшаның әрекеті біріншіге салыстырғанда біршама бұрылған 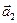векторымен өрнектеледі, өйткені екінші аумақшаның фазасы бірінші аумақша фазасынан өзгеше болады. Ұзындығы бойынша іс жүзінде бұл вектор бірінші қандай болса, сондай, өйткені теңдей аумақшалар туғызатын тербеліс амплитудасы толқын шебінің 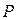нүктесі арқылы жүргізілген сызыққа көлбеулігімен ғана өзгеше болады, ал екі көрші аумақша үшін көлбеудің өзгерісі елеусіз аз болады. Тұрғызуды осылай жалғастырып спираль түріндегі сынық сызық аламыз. 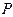нүктесіндегі қорытқы тербеліс О нүктесін ашық аумақтардың ең соңғысынан келетін тербеліске сәйкес 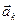векторының соңымен қосатын 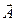векторымен кескінделеді.

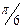Толқын шебі көрші аумақшалар шығаратын тербелістері фазаларының айырымы тұрақты және ол, мысалы, -ға тең болатындай етіліп бөлінген болсын. Алғашқы алты 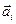векторларының қосындысы 4а-суретте келтірілген. Берілген жағдайда осы векторлардың ең соңғысының фазасы 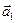векторының фазасына қарама-қарсы болады, яғни қарастырылатын алғашқы алты аумақша Френельдің орталық (нөлінші) аумағына сәйкес келеді. Сонымен 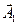векторы Френельдің орталық аумағы туғызатын толқын амплитудасын анықтайды. Осыған ұқсас 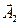векторы (4б-сурет) Френельдің бірінші екі аумағы туғызатын толқын амплитудасын кескіндейді. 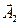векторының ұзындығы осы жағдайда 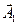ұзындығынан едәуір кіші. Бұл 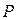нүктесіндегі амплитуда бір аумақ ашық болғанда екі аумақ ашық болғандағыдан үлкен болады деген 3.2 қорытындысына сәйкес келеді. Жалпы ашық аумақтардың санына байланысты 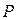нүктесінде тербеліс амплитудасының не үлкен, не кіші мәндерін алатын боламыз. Толығынан ашық толқындық шепке аумақтардың шексіз көп саны сәйкес келеді де, сынық спираль түріндегі сызық асимптотикалық түрде С центріне жақындайтын болады. 4а және 4в-суреттерін салыстырудан 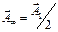болатындығы көрінеді, ал бұл алгебралық қосу нәтижесімен дәл келеді. Егер толқындық шеп шексіз жіңішке аумақшалардың шексіз санына бөлінсе, онда сынық сызық спиральға айналады (5-сурет). Сонымен, 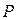нүктесіндегі барлық толқын туғызатын тербеліс фазасы бойынша Френельдің орталық аумағы туғыза алатын тербеліспен дәл келеді, ал амплитудасы бойынша осы тербелістің жарты амплитудасын құрайды.