Френельдің аумақтық әдісі

Жарық дифракциясы. 5 апта.

Электромагниттік толқын бір текті ортада тараған кезде толқын шебінің геометриялық пішіні өзгермейді. Егерде толқын мөлдір емес кедергілері бар немесе сыну көрсеткіші шұғыл өзгеретін аймақтары бар біртекті емес мөлдір ортада таралатын болса, онда толқын шебі бүлінеді, кеңістікте интенсивтіктің үлестірілуі өзгереді. Осындай жағдайларда дифракция деп аталатын құбылыс пайда болады.

Оптикада Френель дифракциясы және Фраунгофер дифракциясы деп дифракция шартты түрде екіге бөлінеді. Френель дифракциясы (сфералық толқындар дифракциясы) Фраунгофер дифракциясына (параллель шоқтар, яғни жазық толқындар дифракциясы) қарағанда жалпы жағдай болып табылады.

Френельдің аумақтық әдісі

Френель дифракциялық суреттерді есептеудің жарты-толқындық аумақтар немесе Френель аумақтары деген көрініске негізделген жуық әдісін ұсынды.

Френель 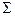толқындық беттің әртүрлі элементтерінен келетін тербелістердің амплитудаларын қосуды 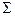бетін конфигурациясы қарастырылып отырған есептің симметриясына қарай аумақтарға бөлу арқылы іске асыруды ұсынды.

Френель әдісін ұғыну үшін мөлдір емес қалқадағы дөңгелек тесіктен кейінгі оның осінің бойында жататын 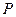нүктесіндегі жарық тербелістерінің амплитудасын анықтайық (1-сурет). Осы есепті Гюйгенс-Френель принципі көмегімен шешу үшін екі жорамал жасалады: 1) қалқаның жарық өткізбейтін бөліктері екінші реттік толқы ндар көзі болмайды; 2) тесіктегі толқын шебінің нүктелері қалқаның мөлдір емес бөліктері болмаған жағдайда қандай екінші реттік толқын көздері болса, дәл сондай көздері болады. Тесікті жабатын 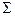толқындық бет SР түзуіне қатысты симметриялы, сондықтан осы бетті центрі тесік осіне келетін сақиналық аумақтарға бөлген жөн. Осы аумақтар әрбір аумақтың шеттерінен 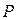нүктесіне дейінгі ара қашықтықтың бір-бірінен айырмашылығы толқын ұзындықтың жартысына (l/2) тең болатындай етіп алынады. Бұл өзі берілген жағдайдағы Френель аумақтары болады.

Аумақтардың шекараларын М₀, М₁, М₂,... арқылы белгілегенде, осы шарт мына түрде жазылады:

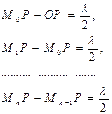(1)

мұндағы l-жарықтың толқыны ұзындығы, 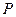- өріс бақыланатын нүкте, О-Френельдік нөлінші аумағының центрі (2-сурет).

Осылай алынған аумақтардың мөлшерін есептейік. Орталық аумақ үшін (2-сурет) .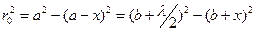

а мен b-ға салыстырғанда l кіші шама (а, b>>l) болуы себепті мынаны табамыз

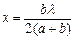(2)

радиусы r₀ cфералық сегменттің ауданы 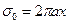болады, немесе (3.4)-ді ескергенде

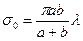(3)

Бірінші екі аумақтан тұратын сегмент ауданы 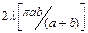болады, яғни екінші аумақтың ауданы да s₀-ге тең және т.т. Сонымен Френель әдісі бойынша тұрғызу толқындық шепті теңдей аумақтарға бөледі, бұлардың әрқайсысының (3) өрнегімен анықталатын ауданы болады. Демек 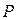нүктесіне дейін жеке аумақтардан келіп жететін тербелістердің амплитудалары b қашықтығына және аумақ бетіне түсірілген 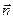нормаль мен b бағыты арасындағы j бұрышқа тәуелді болады. Мұнда ескеретін нәрсе, аумақ нөмірі m өскенде b_m қашықтығы артады және j бұрышы ұлғаяды. Сондықтан жеке аумақтардан 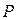нүктесіне дейін жеткен тербелістердің а_m амплитудалары кішірейе беруі тиіс: а₀> a₁ >…> a_m > a_m+1>...

Екі көрші аумақтан 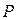нүктесіне келетін тербелістердің фазалары қарама-қарсы болатындықтан, m аумақ әрекеті тудыратын қорытқы тербелістің А_m амплитудасы мынаған тең

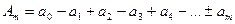(4)

мұндағы соңғы мүшенің таңбасы m тақ болғанда оң, m жұп болғанда-теріс болады. Сірә, аумақ саны жұп болған жағдайда бұлардың әрекеттері қос-қостан бірін-бірі әлсіретеді де, 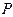нүктесіндегі қорытқы тербелістің А_m амплитудасы елеусіз аз болады. Аумақ саны тақ болғанда бұлардың біреуінің әрекеті әлсіремей қалады да, А_m m жұп болғандағыдан үлкен болады.

Қорытқы тербелістің А_m амплитудасының дәлірек мәнін былай алуға болады. (4) қосындысындағы барлық тақ мүшелерді екі қосылғышқа бөлеміз

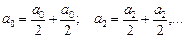
Сонда m тақ болғанда

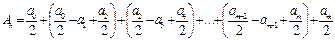(5)

m жұп болғанда

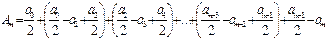(6)

m аумақ нөмірі артқан сайын а_m амплитудалары кішірейе беретін болантындықтан, қандай да бір m аумағы тудыратын тербелістер амплитудасын, жуықтап алғанда, оған көршілес (m-1)-і және (m+1)-і аумақтары тудыратын тербелістердің амплитудалары қосындысының жартысына тең деп алуға болады: 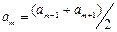. Осының негізінде (5) және (6) теңдіктердің оң жақтарындағы жақшалардың ішіндегі барлық қосындылар нөлге тең болады, демек, m тақ болғанда

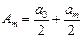(7)

ал m жұп болғанда

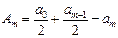(8)

Егер аумақ саны жеткілікті көп болса, (m-1)-і және m-і аумақтар туғызатын тербелістердің амплитудаларының бір-бірінен айырмашылығы аз болады да, жуық түрде 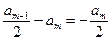деп алуға болады.

Сонымен, (7) және (8) теңдіктері мына түрге келеді

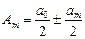(9)

мұндағы “±”- аумақ саны тақ, “-” – аумақ саны жұп болғанда алынады.

Толқындық шептің қалқамен жабылмаған бөлігіне (тесікке) келетін (сиятын) аумақтар саны қалқадағы тесіктің өлшемдеріне (тесік ауданының жеке аумақ ауданына қатынасына), және де бақылау нүктесінің тесіктен қашықтығына (қалқаның орналасқан орнына) тәуелді болады. 3.6-суреттен нөлінші немесе орталық аумақ радиусын оңай табуға болады; ол мынаған тең

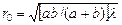(10)

Ал, m-і аумақ радиусы

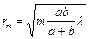(11)

сірә, r_m қалқадағы қарастырылып отырған тесік радиусы болып табылады. Осыдан радиусы 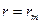тесік толқындық шептің (3.13) өрнегімен анықталатын

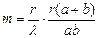(12)

аумақтар саны сиятын бөлігін ашатындығын табамыз.

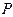нүктесіндегі қосынды тербеліс амплитудасы 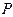бақылау нүктесінің орнымен анықталатын ашық аумақтар санына тәуелді, яғни әртүрлі 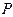нүктелері үшін m саны әртүрлі болады. m тақ болатын 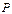нүктелерінде қосынды тербелістің А_m амплитудасы үлкен болады, ал m жұп болатын 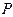нүктелерінде А_m кіші болады. Амплитуда квадраты интенсивтікті анықтайды. Сонымен, 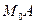түзуі бойымен жылжығанда жарық интенсивтігі өзгеретін болады. Жарық көзінің, тесігі бар қалқаның және 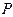бақылау нүктесінің берілген орналасуында 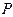нүктесіндегі жарық интенсивтігі тесіктің r мөлшерінен және оның толқын ұзындыққа қатынасына тәуелді болады.

Егерде тесіктің мөлшерін шексіздікке дейін өсіретін болсақ, яғни 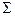толқындық шептің бүкіл бетін ашық қалдыратын болсақ, онда соңғы а_m аумақтың әрекеті шексіз кіші болады да (8) өрнегінен қосынды тербеліс амплитудасы үшін 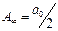шығады, яғни толқындық шеп ашық болған жағдайда барлық толқынның әрекеті орталық аумақтың жартысының әрекетімен пара-пар болады.

Аумақтар саны үлкен болған жағдайда 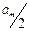кіші болады да, А_m амплитудасының іс жүзінде 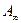амплитудасынан айырмашылығы болмайды. Бұл толқындық шептің толық ашық болуына сәйкес келеді. Осыдан ашық аумақтар саны үлкен болғанда тесік мөлшері 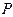нүктесіндегі интенсивтікке әсер етуден қалады. Егерде жарық түзу сызықты таралатын болса, онда тесік мөлшері 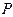нүктесіндегі интенсивтікке ешқандайда әсер етпеуі тиіс еді. Осыдан мынадай салдарға келеміз: толқындық көріністер мен жарықтың түзу сызықты таралуы жөніндегі көріністерден алынатын қорытындылар ашық аумақтар саны үлкен болған жағдайда бірдей бола бастайды. (11) өрнегінен аумақтардың осы санын бағалауға болады. Мысалы, жазық толқындық шеп ( 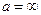) жағдайында радиусы 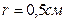тесіктен b=50 см қашықтықта орналасқан 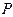нүктесі үшін 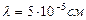болғанда аумақтар саны n=100 болады. Осындай аумақтар саны сиятын тесікті бұдан әрі қарай өсіру 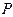нүктесіндегі интенсивтікке әсер етпейді, яғни жарық түзу сызықты таралғандағыдай нәтиже аламыз. 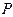нүктесінен радиусы дәл сондай тесікке дейінгі ара қашықтықты 50м-ге дейін өсіргенде тесік ауданына тек бір Френель аумақ сиятын болады да, жарық таралуының толқындық сипаты айқын білінетін болады.