Анализ и оптимизация сетевого графика

После процедуры планирования можно построить так называемую диаграмму GANTT. В этой диаграмме все работы располагаются утолщенными отрезками по горизонтали. Параллельные работы располагаются на разных вертикальных уровнях. Осью Х здесь является время начиная с 0. Связи между работами указываются тонкими линиями со стрелками. В диаграмме GANTT используются ранние времена начала и конца работ. Пример варианта диаграммы GANTT приведен на рис. 5.18.

Рис. 5.18. Пример варианта диаграммы GANTT

По заданным временам событий эта диаграмма строится всеми пакетами сетевого планирования.

После нахождения критического пути и резервов времени работ и оценки вероятности выполнения проекта в заданный срок должен быть проведён всесторонний анализ сетевого графика и приняты меры по его оптимизации. Этот весьма важный этап в разработке сетевых графиков раскрывает основную идею сетевого планирования. Он заключается в приведении сетевого графика в соответствие с заданными сроками и возможностями организации.

Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную.

Видами частной оптимизации сетевого графика являются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта.

Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.

Вначале рассмотрим анализ и оптимизацию календарных сетей, в которых заданы только оценки продолжительности работ.

Анализ сетевого графика начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ, степени их расчленения.

Затем проводятся классификация и группировка работ по величинам резервов. Следует отметить, что величина полного резерва времени далеко не всегда может достаточно точно характеризовать, насколько напряжённым является выполнение той или иной работы некритического пути. Всё зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности.

Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряжённости работ.

Коэффициентом напряжённости работыназывается отношение продолжительности несовпадающих, но заключённых между одними и теми же событиями, отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим — критический путь. Приведем пример. Предположим, имеется событийный граф рис. 5.19.

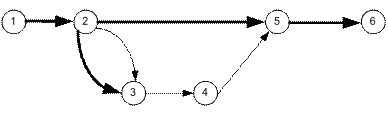
Рис. 5.19. Событийный граф с критическим путем

Критический путь на этом графе изображен жирной линией. Более длительная работа между событиями 2–3 изображена жирной линией. Для определения коэффициента напряженности необходимо, прежде всего, найти вершины графа на критическом пути, на которые осуществляется выход данной работы по стрелкам и против стрелок. В наше простом примере для работы 3–4 это очевидно события 5 и 2. Далее между событиями 4 и 5 определяется максимально возможная длительность К по сетевому графику. В нашем примере только одна работа с длительностью К = 6. Затем между событиями 3 и 2 тоже определяется максимальная длительность Н по сетевому графику. К нашем примере из двух работ более продолжительна работа с длительностью 11 и поэтому Н = 11. Для определения величин К и Н необходимо два раза решить задачи вычисления критического пути между соответствующими вершинами графа. И, наконец определяется длина критического пути КК между работами 2 и 5 (в нашем примере КК = 30). Коэффициент напряженности kn_3,4 работы 3–4 вычисляется по формуле:

=

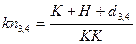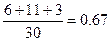
где: d_3,4 – длительность работы 3–4.

Этот коэффициент может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путём, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути).

Обратим внимание на то, что больший полный резерв одной работы по сравнению с другой не обязательно свидетельствует о меньшей степени напряжённости её выполнения. Это объясняется разным удельным весом полных резервов работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путём.

Вычисленные коэффициенты напряжённости позволяют дополнительно классифицировать работы по зонам:

ú критическая: К > 0/8,

ú подкритическая: 0.6 < К < 0.8,

ú резервная: К < 0.6.

Оптимизация сетевого графикапредставляет процесс улучшения организации выполнения комплекса работ с учётом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряжённости работ, рационального использования ресурсов.

В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается:

q Перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических, при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряжённых, в зоны, объединяющие наиболее напряжённые работы.

Например, можно увеличить сменность работ на «узких» участках строительства. Это мероприятие наиболее эффективно, поскольку позволяет добиться нужного результата при тех же ведущих машинах (экскаваторе, станке и т. д.), только увеличив численность рабочих.

q Сокращением трудоёмкости критических работ за счёт передачи части работ на другие пути, имеющие резервы времени.

q Пересмотром топологии сети, изменением состава работ и структуры сети.

q Обеспечить проведение параллельных (совмещенных) работ.

q Разделить широкий фронт работ на более мелкие.

q Уменьшить продолжительность программы можно путем изменения применяемой технологии.

Проводя корректировку графика надо иметь в виду, что рабочих насыщают ресурсами до определенного предела (чтобы каждый рабочий был обеспечен достаточным фронтом работ и имел возможность соблюдать правила техники безопасности).

В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути и так будет продолжиться до получения удовлетворительного результата.

Самый очевидный вариант частной оптимизации сетевого графика с учётом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности. Продолжительность каждой работы целесообразно увеличить на величину такого резерва, чтобы не изменить ранние сроки наступления всех событий сети, то есть на величину свободного резерва времени.

На практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительно к оценкам сроков фактора стоимости работ. Проект может потребовать ускорения его выполнения, что, естественно, отразится на стоимости: она увеличится. Поэтому необходимо определить оптимальное соотношение между стоимостью проекта и продолжительностью его выполнения.

При использовании метода «время–стоимость» предполагают, что уменьшение продолжительности работы пропорционально возрастанию её стоимости. Возрастание стоимости при уменьшении времени называется затратами на ускорение.

Весьма эффективным является использование метода статистического моделирования, основанного на многократных последовательных изменениях продолжительности работ (в заданных пределах) и «проигрывании» на компьютере различных вариантов сетевого графика с расчётами всех его временных параметров и коэффициентов напряжённости работ.

Например, можно взять в качестве первоначального план, имеющий минимальные значения продолжительности работ и, соответственно, максимальную стоимость проекта. Затем последовательно увеличивать продолжительность выполнения комплекса работ путём увеличения продолжительности работ, расположенных на некритических, а затем и на критическом (критических) пути до удовлетворительного значения стоимости проекта. Соответственно, можно взять за исходный план, имеющий максимальную продолжительность работ, а затем последовательно уменьшать их продолжительность до такого приемлемого значения продолжительности проекта.

Процесс «проигрывания» продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности улучшения плана исчерпаны и поставленные перед разработчиком проекта условия невыполнимы.

В настоящее время на практике сеть вначале корректируют по времени, т.е. приводят ее к заданному сроку окончания строительства. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.

Следует заметить, что при линейной зависимости стоимости работ от их продолжительности задача построения оптимального сетевого графика может быть сформулирована как задачалинейного программирования, в которой необходимо минимизировать стоимость выполнения проекта при ограничении, во-первых, продолжительности каждой работы в установленных пределах, а, во-вторых, продолжительности любого полного пути сетевого графика не более установленного срока выполнения проекта.

В настоящее время практически не формализована задача оптимизации сетевого графика по критерию ресурса. Эта задача часто требует переформирования сетевого графа в соответствии с правилами параллельного выполнения работ и пока не формализована.