Система сбалансированных показателей (BSC) эффективности

BSC представляет собой схему для перевода общей стратегии компании в термины операционного процесса. Задача BSC — трансформировать миссию компании в конкретные, вполне осязаемые задачи и показатели.

Цели и показатели данной системы формируются в зависимости от мировоззрения и стратегии каждой конкретной компании и рассматривают ее деятельность по четырем критериям: финансовому, взаимоотношениям с клиентами, внутренним бизнес-процессам, обучению и развитию персонала.

Система сбалансированных показателей имеет следующие преимущества:

q делает корпоративное видение будущего достоянием всех сотрудников и способствует установлению атмосферы единомыслия;

q создает целостную модель стратегии, что позволяет каждому работнику определить свой вклад в достижение успеха компании;

q позволяет сконцентрировать усилия: если цели и показатели выбраны правильно, успех обеспечен; если нет, то все инвестиции и инициативы напрасны;

q тесно связана со стратегией компании.

При построении BSC используют следующие принципы: причинно-следственные связи, факторы достижения результатов, взаимосвязь с финансовыми результатами.

Система BSC представляет собой комплекс показателей результатов и факторов деятельности. Правильно составленная BSC должна иметь сбалансированный комплекс результатов и факторов достижения результатов.

Выделяют четыре составляющих BSC:

q финансовую — рентабельность инвестиций и добавленная стоимость;

q клиентскую — удовлетворение потребностей клиента, сохранение клиентской базы и доли рынка;

q бизнес-процессы — качество, сроки исполнения заказа, стоимость, разработка новых продуктов и услуг;

q обучение — удовлетворенность персонала и наличие информационных систем.

Сетевое планирование

Материал подготовлен с использование работы: webforum.land.ru.

Методики сетевого планирования были разработаны в конце 50-х годов в США.

Однако первые ЭВМ были дороги и доступны только крупным организациям. Таким образом, исторически первые проекты представляли из себя грандиозные по масштабам работ, количеству исполнителей и капиталовложениям государственные программы.

В настоящее время сложились глубокие традиции использования систем управления проектами во многих областях жизнедеятельности

Сущность и назначение сетевого планирования и управления

Недостатки линейного календарного графика в значительной мере устраняются при использовании системы сетевых моделей, которые позволяют анализировать график, выявлять резервы и использовать электронно-вычислительную технику.

Весь процесс находит отражение в графической модели, называемой сетевым графиком. В сетевом графике учитываются все работы от проектирования до ввода в действие, определяются наиболее важные, критические работы, от выполнения которых зависит срок окончания проекта. В процессе деятельности появляется возможность корректировать план, вносить изменения, обеспечивать непрерывность в оперативном планировании. Существующие методы анализа сетевого графика позволяют оценить степень влияния вносимых изменений на ход осуществления программы, прогнозировать состояние работ на будущее. Сетевой график точно указывает на работы, от которых зависит срок выполнения программы.

Основные элементы сетевого планирования и управления

Сетевое планирование и управление — это совокупность расчётных методов и контрольных мероприятий по планированию и управлению комплексом работ с помощью сетевого графика.

Сетевая модель — это план выполнения некоторого комплекса взаимосвязанных работ, заданного в форме сети, графическое изображение которой называется сетевым графиком.

Главными элементами сетевой модели являются работы и события.

Под событие понимается момент начала и момент окончания работы. Событие не имеет временной длительности.

Событие может свершиться только тогда, когда закончатся всё работы, ему предшествующие по сетевому графику. Для всех непосредственно предшествующих событию работ оно является конечным, а для всех непосредственно следующих за ним — начальным.

Каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Под работой понимается процесс, имеющий временную длительность.

Во-первых, это действительная работа — протяжённый во времени процесс, требующий затрат. Каждая действительная работа должна быть конкретной, чётко описанной и иметь ответственного исполнителя. Во-вторых.

Во вторых, это ожидание — протяжённый во времени процесс, не требующий затрат труда.

В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Фиктивная работа отражает только тот факт, что одна работа не может быть начата раньше, чет закончится другая работа. Продолжительность фиктивной работы принимается равной нулю.

Сетевая модель сетевого графика может задаваться в двух интерпретациях:

q в виде событийного графа (графа, основанного на событиях; CRM-диаграмма) ;

q в виде вершинного графа(графа, основанного на работах; PERT-диаграмма) .

Сетевые графики составляются на начальном этапе планирования. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумываются их логические связи и последовательность выполнения, работы закрепляются за ответственными исполнителями. С их помощью и с помощью нормативов, если таковые существуют, оценивается продолжительность каждой работы. Затем составляется (сшивается) сетевой график. После упорядочения сетевого графика рассчитываются параметры событий и работ, определяются резервы времени и критический путь. Наконец, проводятся анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчётом параметров событий и работ.

Формирование событийного графа.

При формировании событийного графаиспользуются следующие обозначения.

События в событийном графе изображаются кружками (вершины графа) с указанием номера события. Все вершины в пределах графа должны иметь разные номера. Нумеровать вершины можно в произвольном порядке без пропуска номеров, начиная с 1. Пример вершины-события приведен на рис. 5.11.

Рис. 5.11. Пример вершины событийного графа

Работы в событийном графе изображаются однонаправленными стрелками. Фиктивная работа изображается пунктирной линией. Эти линии в теории графов называются ребрами, а такой граф – направленным графом. Рядом с ребром необходимо указать длительность работы.

При формировании событийного графа нужно выполнить определенные требования:

q граф должен иметь только одну начальную вершину;

q граф должен иметь только одну конечную вершину;

q в графе не должно быть петель, т. е. ребер с началом и концом в одной вершине;

q в графе не должно быть циклов, т. е. путь из начальной вершины графа по стрелкам и любому пути всегда приводит к конечной вершине графа;

q любые две вершины, т. е. два события, желательно должны иметь только одно ребро, т. е. одну работу. Это условие не обязательное.

Наиболее часто в сложной структуре графа делается ошибка с циклами. Эту ошибку невозможно обнаружить на компьютере и, поэтому надо очень внимательно готовить граф. Если в графе окажутся циклы, то программы сетевого планирования просто или зациклятся или выдадут неверный результат.

Пример событийного графа приведен на рис. 5.12.

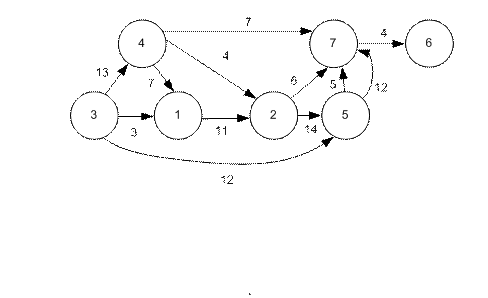
Рис. 5.12. Пример событийного графа

Пример неверного графа с циклом приведен на рис. 5.13.

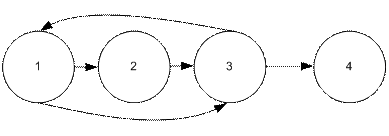
Рис. 5.13. Ошибочный граф с циклом

Сетевые графики на основе событийного графа получили наибольшее распространение. Это, прежде всего, связано с очень хорошей математической проработкой сетевого планирования на основе этих графов. Такие графы наиболее понятны профессионалам-математикам.

На практике используется изображение графа без указания номеров узлов и длительностей работ. Если в сетевой модели нет числовых оценок, то такая сеть называется структурной. Однако для расчетов необходимо использовать сети, в которых заданы оценки продолжительности работ, а также оценки других параметров, например трудоёмкости, стоимости и т. п.

Если сеть имеет одну конечную цель, то сеть называется одноцелевой. Сетевой график, имеющий несколько завершающих событий, называется многоцелевым. Многоцелевые сети и не могут быть рассчитаны по одному алгоритму. Расчет здесь ведется относительно каждой конечной цели. Примером может быть строительство жилого микрорайона, где ввод каждого дома является конечным результатом, и в графике по возведению каждого дома определяется свой критический путь. Однако, при раздельном расчете по каждой конечной цели могут оказаться не совпадающие в общей части графа критические пути. В связи с этим, если проект единый, то конечные узлы такого графа нужно соединить фиктивными работами. Направление ребра фиктивной работы указывается произвольным и от этого направления результат сетевого планирования не зависит.

В событийном графе нет необходимости указывать работу-ожидание. Если в ее указании есть острая необходимость, то такая работа указывается как обычная работа. Указание работы-ожидания может быть возможным в графе с несколькими началами и известными временными интервалами между этими началами.

Формирование вершинного графа.

Событийный граф не пользуется вниманием среди профессиональных экономистов, т. к. он им менее понятен, чем вершинный граф.

Вершинный граф строится на основе взаимодействия работ друг с другом. Вершиной в этом графе является работа, а ребром – связь одной работы с другой. Для экономистов такая структура понята, т.к. необходимо задавать связи одной работы с другой.

Работа в вершинном графе задается вершиной графа, т.е. в виде окружности, как и в стрелочном графе. Все вершины нумеруются, начиная с 1 и без пропуска номеров. Граф не должен иметь вершин с одинаковыми номарами. Рядом с вершиной указывается длительность работы. Фиктивные работы в вершинном графе не задаются, т. к. здесь это не имеет смысла.

Связь одной работы с другой задается направленным ребром графа. Ребро такого графа отражает только факт связи двух работ и, поэтому на ребре не указывается никакой длительности и ребра не нумеруются.

Пример вершинного графа, соответствующего событийному графу рис. 5.12, приведен на рис. 5.14.

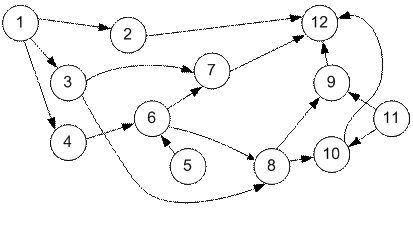
Рис. 5.14. Пример вершинного графа

Примечательно то, что вершинный граф легко получить на основании событийного графа. Для этого надо в событийном графе ребро мысленно представить точкой и нарисовать взаимодействие полученных точек на основании событийного графа. Получить же, наоборот, событийный граф на основании вершинного - очень не просто. В связи с этим лучше всего первым изображать событийный граф.

В вершинном графе может быть несколько начальных и конечных вершин-работ. Единственным условием корректности графа является нулевое время начала всех начальных работ и одно время завершения всех конечных работ. Многоцелевой вершинный граф задать, в отличие от событийного, невозможно без дополнительных словесных пояснений. Этот факт продемонстрирован на рис. 5.15.

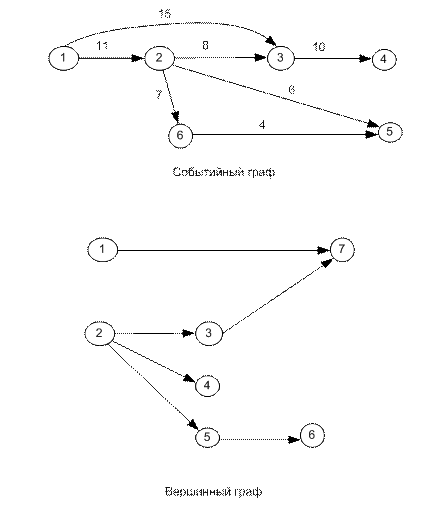
Рис. 5.15. Пример многоцелевого событийного графа и соответствующего вершинного

Как следует из рис. 5.15, в вершинном графе нет однозначности в неодновременном окончании всех работ и, поэтому будет считаться, что работы заканчиваются одновременно.

Сетевое планирование на основе вершинного графа имеет более сложную математическую реализацию в общем случае. Расчет критического пути сетевого графика, с одной стороны, здесь имеет более простой алгоритм реализации. С другой стороны, вычисление ранних о поздних начальных и конечных времен в вершинном графе реализуется со значительно более непонятным и сложным алгоритмом.

Сети на основании работ оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (показатель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления комплексом.