Амплитуда, интенсивность, мощность.
Нередко несколько источников соединяются для получения суммарной мощности. Рассмотрим условия согласования нагрузки для этого случая.
Возьмем хорошо известный пример. Имеется два источника гармонических колебаний одной частоты: u1=U1cos(ωt−φ1) и u2=U2cos(ωt−φ2).
Сумма этих колебаний равна: u=u1+u2=U1cos(ωt−φ1)+U2cos(ωt−φ2). Учитывая, что Ucos(ωt-φ)=Ucosωt cosφ+Usinωt sinφ,запишем эту сумму в виде:
u=(U1 cosφ1+U2 cosφ2 ) cosωt+(U1 sinφ1+U2 sinφ2 ) sinωt.
Обозначим выражения, заключенные в скобки:
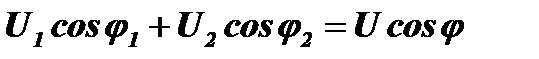 ,
,
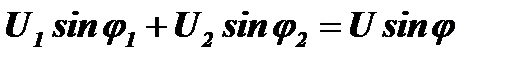 .
.
Тогда суммарное колебание можно представить в виде гармонического колебания: u=Ucosφ∙cosωt+Usinφ∙sinωt=Ucos(ωt−φ). Найдем амплитуду U и фазу φ этого колебания.
Чтобы найти амплитуду U возведем эти уравнения в квадрат и сложим. В результате получим выражение для квадрата амплитуды: 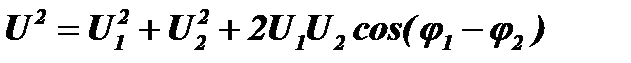 . Величина U2 всегда положительна или равна нулю, так как cos(φ1-φ2)≥−1.
. Величина U2 всегда положительна или равна нулю, так как cos(φ1-φ2)≥−1.
Разделив эти уравнения одно на другое, получим выражение, из которого можно найти фазу φ: 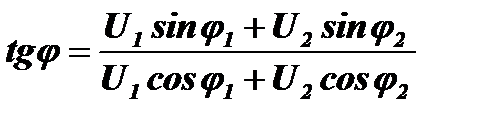 .
.
Рассмотрим случай синфазного сложения колебаний двух источников с одинаковой амплитудой, положив U1=U2, а φ1–φ2=0. В этом случае максимальное значение квадрата амплитуды будет равно 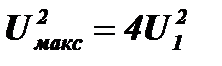 .
.
Обратим внимание на эту формулу. Нередко на её основании делается вывод о том, что при удвоении амплитуды колебаний, мощность суммарного процесса увеличивается в четыре раза. Это неверно, поскольку величина 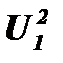 не является мощностью. Эта величина называется интенсивностью источника. Чтобы из интенсивности получить мощность, отдаваемую источником, необходимо разделить её на сопротивление нагрузки. В литературе часто используется такой прием: в качестве нагрузки используется сопротивление в один Ом. В этом случае U2=Р. Формально так поступить можно, но при этом мы должны помнить, что условия согласования внутреннего сопротивления источника и сопротивления нагрузки нарушаются.
не является мощностью. Эта величина называется интенсивностью источника. Чтобы из интенсивности получить мощность, отдаваемую источником, необходимо разделить её на сопротивление нагрузки. В литературе часто используется такой прием: в качестве нагрузки используется сопротивление в один Ом. В этом случае U2=Р. Формально так поступить можно, но при этом мы должны помнить, что условия согласования внутреннего сопротивления источника и сопротивления нагрузки нарушаются.
Чтобы найти мощность, отдаваемую суммируемыми источниками в нагрузку, рассмотрим схему сложения приведённых выше синфазных колебаний с равными амплитудами U1=U2=U на активной нагрузке. На рис.6.9,а показан источник одного колебания с амплитудой U, имеющий внутреннее сопротивление 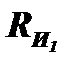 , нагруженный на согласованную нагрузку
, нагруженный на согласованную нагрузку 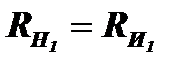 и выделяющий в ней максимальную мощность
и выделяющий в ней максимальную мощность 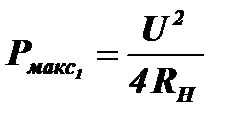 .
.
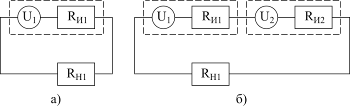
Рис. 6.9
Теперь для получения удвоенной мощности 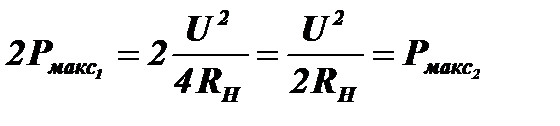 введём в схему второй источник синфазного колебания с такой же амплитудой U и с таким же внутренним сопротивлением
введём в схему второй источник синфазного колебания с такой же амплитудой U и с таким же внутренним сопротивлением 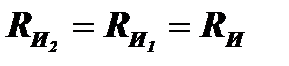 (рис.6.9, б). Если не менять сопротивление нагрузки, то при максимальной амплитуде колебаний U+U=2U в цепи будет протекать ток I=2U/3RН и максимальная мощность будет равна:
(рис.6.9, б). Если не менять сопротивление нагрузки, то при максимальной амплитуде колебаний U+U=2U в цепи будет протекать ток I=2U/3RН и максимальная мощность будет равна:
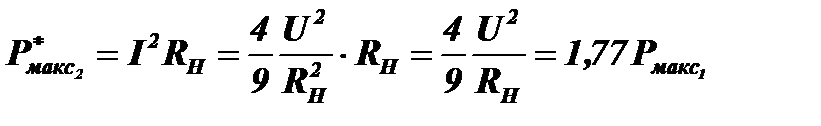 .
.
Теперь согласуем нагрузку, положив 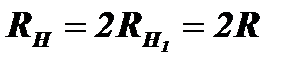 . Тогда ток I=2U/4RН=U/2RН , а максимальная мощность станет равна:
. Тогда ток I=2U/4RН=U/2RН , а максимальная мощность станет равна:
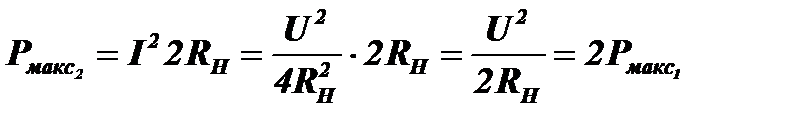
Таким образом, при удвоении амплитуды гармонических колебании максимальное значение мощности суммарного колебания, которое можно получить в согласованной нагрузке, также возрастёт в два раза, а не в четыре.
Выше мы рассматривали случаи, когда от источника в нагрузку необходимо передать максимальную мощность.
Однако на практике часто используются источники, от которых требуется не передать максимальную мощность, а сохранять при изменении нагрузки свое напряжение (источники напряжения) или потребляемый ток (источники тока). Такие источники имеют большой запас собственной мощности по сравнению с той, которая от них потребляется нагрузкой. В этом случае источник рассогласован с нагрузкой, а внутреннее сопротивление источника либо очень мало по сравнению с сопротивлением нагрузки или, наоборот, очень велико.
Рассмотрим эти два случая для схем, имеющих только активные сопротивления, используя рис. 6.9,а.
При RН>>RИ схема является источником напряжения. В этом случае R=RН+RИ»RН и при изменении сопротивления нагрузки ток 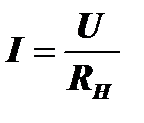 меняется, а падение напряжения на нагрузке UНАГР=IRН=
меняется, а падение напряжения на нагрузке UНАГР=IRН= 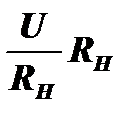 »U равно напряжению источника и не зависит от этого сопротивления. В этом случае мощность, отдаваемая источником в нагрузку, будет равна:
»U равно напряжению источника и не зависит от этого сопротивления. В этом случае мощность, отдаваемая источником в нагрузку, будет равна:
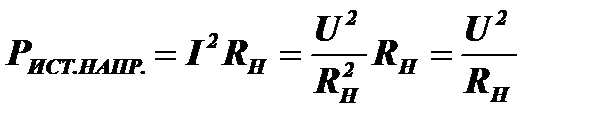 <<Pмакс,
<<Pмакс,
поскольку RН в этом случае намного больше, чем RН при согласованной нагрузке.
Если в этой схеме удвоить амплитуду напряжения, то ток станет равен 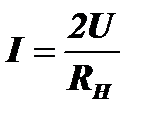 , а мощность, отдаваемая источником в нагрузку, станет равна
, а мощность, отдаваемая источником в нагрузку, станет равна 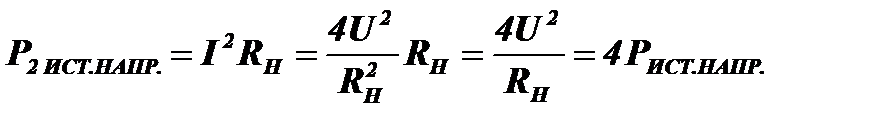 Таким образом в этом случае при удвоении напряжения получена учетверенная мощность, но это не максимальная мощность, которую можно получить от источника, а та небольшая мощность, которую источник отдает в нагрузку при значительном рассогласовании своего внутреннего сопротивления и нагрузки.
Таким образом в этом случае при удвоении напряжения получена учетверенная мощность, но это не максимальная мощность, которую можно получить от источника, а та небольшая мощность, которую источник отдает в нагрузку при значительном рассогласовании своего внутреннего сопротивления и нагрузки.
Типичным источником напряжения является электростанция, снабжающая город электроэнергией. В этом случае сопротивление всех городских нагрузок обычно значительно превосходит сопротивление генераторов электростанции, что позволяет поддерживать постоянное напряжение в городе, но не позволяет передавать максимум энергии.
При RН<<RИ схема является источником тока. В этом случае R=RН+RИ»RИ и при изменении сопротивления нагрузки падение напряжения на нагрузке UНАГР=IRН= 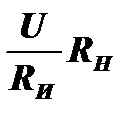 изменяется, а ток
изменяется, а ток 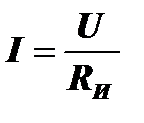 остается постоянным. В этом случае мощность, отдаваемая источником в нагрузку будет равна
остается постоянным. В этом случае мощность, отдаваемая источником в нагрузку будет равна 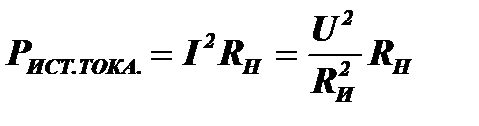 <<Pмакс, поскольку RИ в этом случае намного больше, чем RН.
<<Pмакс, поскольку RИ в этом случае намного больше, чем RН.
Если в этой схеме также удвоить амплитуду напряжения, то при токе 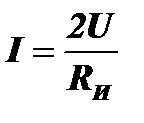 мощность, отдаваемая источником в нагрузку, будет равна
мощность, отдаваемая источником в нагрузку, будет равна 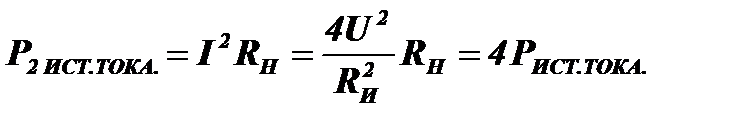 . Таким образом, и в этом случае при удвоении напряжения получена учетверенная мощность, но также, как и в предыдущем случае, это не максимальная мощность, а небольшая доля мощности, отдаваемой в нагрузку при рассогласовании внутреннего сопротивления источника и нагрузки.
. Таким образом, и в этом случае при удвоении напряжения получена учетверенная мощность, но также, как и в предыдущем случае, это не максимальная мощность, а небольшая доля мощности, отдаваемой в нагрузку при рассогласовании внутреннего сопротивления источника и нагрузки.
Следует отметить, что КПД системы в этих случаях будет существенно превышать 50%.
Теперь рассмотрим процессы, происходящие в антенне при сложении принимаемых ею полей. Положим, что при некоторой амплитуде электромагнитного поля Е1, падающего на антенну, её сопротивление излучения согласовано с входным сопротивлением приёмника.
Поле Е1 вызывает в антенне ЭДС U1 и в нагрузке выделяется мощность 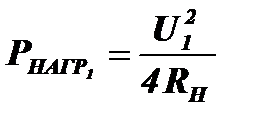 . Такая же мощность PИЗЛ=PНАГР излучается антенной.
. Такая же мощность PИЗЛ=PНАГР излучается антенной.
Рассмотрим, что произойдёт в антенне и её нагрузке, если на антенну дополнительно упадетполе второго источника, синфазного с первым, в результате чего амплитуда электромагнитного поля удвоится Е2=2Е1 и, соответственно, удвоится напряжение в антенне U2=2U1.
В разобранном ранее примере для электрической цепи, удвоение напряжения источника происходило за счёт введения в цепь второго источника напряжения, имеющего своё, дополнительное для данной цепи, внутреннее сопротивление. При удвоении напряжённости поля, падающего на приёмную антенну, никакого видимого дополнительного сопротивления в антенну не вносится. Если это действительно так, то нагрузка (входная цепь приёмника) остаётся согласованной с сопротивлением излучения антенны и в ней должна выделиться мощность: 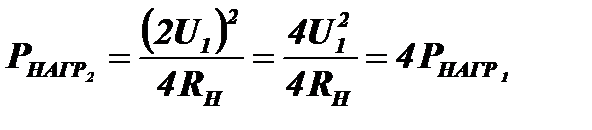 . Таким образом, мощность должна возрасти в четыре раза.
. Таким образом, мощность должна возрасти в четыре раза.
Попытаемся найти объяснение этого парадокса на качественном уровне. При увеличении амплитуды электромагнитного поля увеличивается индуцируемый в антенне ток и увеличивается искривленная область поля, возникающего вокруг антенны (рис.6.8.). В результате возрастает и площадь, с которой диполь собирает энергию падающего на него поля. Это означает, что эффективное сечение диполя увеличилось. Но эффективное сечение антенны входит в формулу для сопротивления излучения в числителе, а это означает, что при увеличении амплитуды поля увеличивается и сопротивление излучения. Поскольку сопротивление излучения для приёмной антенны играет такую же роль, какую играет внутреннее сопротивление источника для электрической цепи, то, очевидно, что сохраняется общая закономерность: при увеличении напряжения источника (в нашем случае амплитуды электромагнитного поля), возрастает и его внутреннее сопротивление (в нашем случае сопротивление излучения антенны). Чтобы сохранить условие согласования сопротивлений источника и нагрузки для передачи максимальной мощности, необходимо увеличить сопротивление нагрузки (входной цепи приёмника).
В этом случае удвоение амплитуды поля, так же как и ранее, приведет к удвоению мощности, выделяемой в нагрузке, а не к увеличению её в четыре раза.
Вывод о том, что величина сопротивления излучения меняется при изменении амплитуды поля, не является строгим и сделан на основании анализа физических закономерностей. Это не должно вызывать недоумения. Необходимо помнить, что сопротивление излучения является условной величиной, определяемой, как эквивалент активного сопротивления, на котором при токе, равном току в диполе, поглощается мощность, равная мощности излучения диполя. А так как при приеме ток в диполе зависит от амплитуды падающего на него электромагнитного поля, то и сопротивление излучения антенны должно зависеть от этой амплитуды.
Дата добавления: 2016-04-19; просмотров: 4573;
