Различие между частотой сигнала и частотой гармоники спектра
В радиотехнических приложениях «частота» является одним из наиболее распространенных терминов. Именно по этой причине возникают недоразумения и даже ошибки, поскольку предполагается, что "частота она и есть частота" и везде она означает одно и тоже понятие. Однако следует строго различать частоту сигнала, который мы анализируем, от частоты гармоники его спектра, которая получается в результате спектрального анализа. Эти частоты образуются по-разному. Мы уже видели, например, что в спектре радиоимпульсного сигнала может не оказаться гармоники с его собственной частотой. Дело в том, что частота сигнала образуется там, где формируется сигнал, а частота гармоники спектра образуется в анализаторе спектра и для ее образования необходимо определенное время. Если вспомнить, что фазой называется аргумент синуса (или косинуса), а частотой – производная этого аргумента, то можно записать:
– для сигнала U(t)cos[wt+j(t)] фаза равна F(t)=wt+j(t), а частота – dF/dt=w+dj/dt=w(t);
– для гармоники спектра Ancos(nwt+jn) фаза равна F(t)=nwt+jn, а частота dF/dt=nw.
Таким образом, частота сигнала может меняться и поэтому нередко называется мгновенной частотой, а частота гармоники всегда постоянна.
Рассмотрим два примера, показывающие, как важно грамотно использовать спектральное представление сигналов.
Первый пример касается построения радиолокационного измерителя высоты (альтиметра) для самолетов. Такой альтиметр излучает непрерывный частотно модулированный сигнал. Отразившись от земли, сигнал возвращается на борт самолета с задержкой по времени, зависящей от расстояния до земли, то есть высоты. Таким образом, частота излучаемого сигнала отличается от частоты принятого сигнала на величину, определяемую этой задержкой (или высотой самолета). При сложении излучаемого и принятого сигналов получаются биения, частота которых Wб зависит от разности частот этих сигналов. Подавая биения на детектор и измеряя частоту огибающей, можно определить высоту полета.
В свое время эта идея вызвала суровую критику приверженцев спектрального анализа. Они утверждали, что альтиметр работать не будет по следующим причинам. Излучаемый частотно модулированный периодический сигнал имеет совершенно определенный дискретный спектр. Отраженный от земли сигнал является копией излучаемого сигнала, сдвинутой на некоторый отрезок времени. Известно, что от сдвига во времени спектр сигнала не меняется. Поэтому сумма излученного и отраженного сигналов будет иметь такой же спектр, как исходный сигнал и в нем не будет никаких разностных частот.
Сейчас очевидно, что в данном случае смешаны понятия частоты сигнала и частоты его гармоники, а в свое время неверный подход привел к остановке проекта и другим, связанным с этим, неприятным последствиям.
Второй пример является не менее показательным.
Важнейшей проблемой радиосвязи является уплотнение эфира и размещение возможно большего числа радиостанций в заданной полосе частот без взаимных помех. Появление частотной модуляции обострило эту проблему, поскольку ЧМ сигналы, повышая качество передач, занимают в эфире значительно более широкие полосы частот, чем сигналы с амплитудной модуляцией.
В связи с этим уже на самых ранних этапах развития методов ЧМ предлагались проекты уплотнения эфира с помощью узкополосной ЧМ. Суть этих проектов сводилась к следующему.
При использовании ЧМ частота передатчика wпер модулируется полезным сигналом с некоторой частотой Wм. Частота Wм определяет «скорость» изменения частоты wпер. Отклонение этой частоты в обе стороны от среднего значения обозначается 2Dwд и называется девиацией частоты. Девиация частоты определяет «амплитуду» изменения частоты wпер. Очевидно, что и девиация частоты Dwд и частота модуляции Wм определяют полосу частот, занимаемую линией связи в эфире.
Для получения узкополосной ЧМ в упомянутых выше проектах предлагалось входной контур приемника настроить так, чтобы несущая частота передатчика wпер попала на крутой склон его резонансной кривой (рис. 5.8).
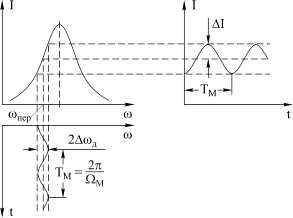
Рис. 5.8
Тогда частотная модуляция входного сигнала преобразуется контуром в амплитудную модуляцию и далее сигнал можно обрабатывать с помощью амплитудного детектора. Предполагалось, что уменьшая полосу пропускания входного контура, то есть увеличивая крутизну склона его частотной характеристики, можно уменьшать девиацию частоты 2Dwд, сохраняя глубину амплитудной модуляции и обеспечивая тем самым практически беспредельное уплотнение эфира при любых значениях модулирующей частоты сигнала Wм.
Однако при реализации этого метода необходимо учитывать инерционность колебательного контура, являющегося преобразователем частотной модуляции в амплитудную. Дело в том, что резонансная кривая колебательного контура, которая осуществляет это преобразование, существует только в установившемся режиме. Она формируется не мгновенно, а за период времени, превышающий постоянную времени контура. Поэтому, если частота Wм модулируется так быстро, что период модуляции Тм=2p ¤ Wм будет значительно меньше, чем постоянная времени входного контура приемника t0,то необходимые значения амплитуд не успеют устанавливаться в узкополосном контуре. Это приведет к сглаживанию модуляции и, следовательно, ее искажению, которое будет тем больше, чем сильнее будет неравенство Тм<t0. Для получения неискаженной модуляции на выходе узкополосного контура в этом случае должно быть выполнено условие Тм>>t0. А это условие нередко забывалось при проектировании, так называемой, узкополосной ЧМ.
Рассмотрим простой пример. Предположим, что несущая частота fпер=1000 кГц. Эта частота модулируется полезным сигналом с частотой Fм=10 кГц. Входной контур приемника имеет добротность Q=300. Тогда период модуляции Тм = 100 мкс, при постоянной времени контура t0=Q¤ p¦пер=100 мкс. Очевидно, что при равенстве этих величин стационарный режим не сможет установиться в контуре приемника, что и приведет к искажениям. А ведь значение добротности Q=300 является относительно небольшим и не может обеспечить достаточно большой крутизны частотной характеристики входного контура приемника. При повышении добротности контура для увеличения этой крутизны сглаживание модуляции и искажение сигнала будут еще больше.
Рассмотренный процесс имеет полную аналогию с процессом получения физического спектра в колебательном контуре анализатора спектра. В обоих случаях, чтобы получить сигнал (или спектр) с требуемым качеством, необходимо время для его установления, значительно превышающее постоянную времени контура. Математический спектр «устанавливается» мгновенно и поэтому никак не учитывает эту особенность, что и приводит к парадоксам.
Дата добавления: 2016-04-19; просмотров: 1653;
