Согласованная фильтрация сигнала в шуме.
Теперь рассмотрим более сложный случай, когда необходимо передать максимум мощности от источника к нагрузке не на одной частоте, а в диапазоне частот. Этот случай является типичной для радиотехники задачей выделения сигнала uс(t), имеющего в некоторой полосе частот спектр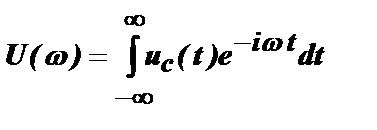 
, из его смеси с шумом uш(t). Упрощённая схема радиосистемы для этого случая приведена на рис. 6.5. Источником сигнала в данном случае является формирующий фильтр с частотной характеристикой S(ω). При возбуждении этого фильтра коротким импульсом на его выходе формируется сигнал со спектром U(ω), который усиливается в передатчике и излучается в пространство. На приёмной стороне этот сигнал вновь усиливается и попадает в согласованный фильтр, который является нагрузкой и имеет частотную характеристику H(ω). Наша задача – найти H(ω), позволяющую получить на выходе этого фильтра максимальную мощность сигнала, а, следовательно, и максимальное отношение сигнал/шум. При рассмотрении этой схемы предполагаем, что все остальные звенья (антенны, пространство, передатчик, приемник) достаточно широкополосны и не вносят изменений в спектр выходного сигнала формирующего фильтра.
Рассмотрим некоторые предположения относительно характера шума, который попадает в согласованный фильтр вместе с сигналом. Если шум стационарный, распределение его произвольно, а зависимость его спектральной плотности от частоты известна и равна Nш(ω), то фильтр, выделяющий сигнал из смеси с таким шумом, называется оптимальным. Если шум имеет нормальное (гауссово) распределение, то его спектральная плотность в полосе частот от 0 до +¥ (в том числе и в полосе частот фильтра) полагается постоянной и равной N Вт/Гц. Если спектры сигнала и шума представлены в комплексной форме, то спектральная плотность нормального шума рассматривается в полосе частот от −¥ до +¥. В этом случае его спектральная плотность принимается равной N/2 Вт/Гц. Фильтр, выделяющий сигнал из смеси с нормальным шумом, называется согласованным.
Спектр сигнала на выходе согласованного фильтра (по напряжению) определяется произведением U(ω)H(ω). Являясь сомножителем этого произведения, частотная характеристика фильтра может изменять этот спектр: некоторые участки подчёркивать, увеличивать, а некоторые, наоборот, сглаживать, уменьшать. Эта роль H(ω) имеет основное значение. Чтобы найти сигнал на выходе фильтра uс(t)вых, необходимо применить к спектру U(ω)H(ω) обратное преобразование Фурье:
.
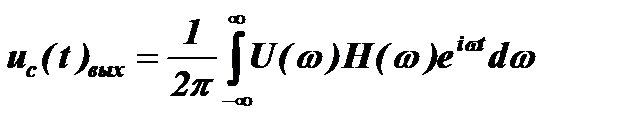Мощность этого сигнала на выходе фильтра равна:
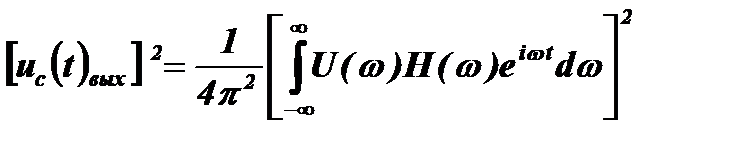
Если шумовое напряжение имеет нормальное распределение, то спектральная плотность мощности шума на выходе фильтра определяется выражением: N·H2(ω), а мощность шума будет равна: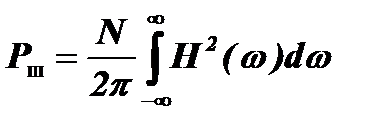 
.
Отношение сигнал/шум представляет практический интерес в момент t0, когда на выходе фильтра формируется максимум сигнала uc(t0)вых=U(t0).Поскольку начало отсчета времени может быть выбрано произвольно, будем полагать t0=0.
Тогда отношение сигнал / шум по мощности примет вид:
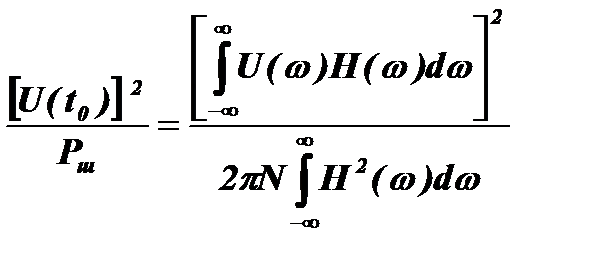
Чтобы найти максимальное значение этого отношения, используем известное из математики неравенство Буняковского-Шварца, которое в общем случае имеет вид:
.
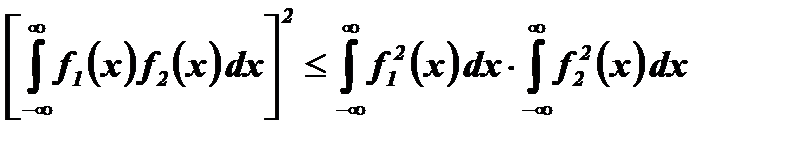Это неравенство превращается в равенство при f1(х)=f2(x). Если входящие в него функции являются комплексными, то неравенство переходит в равенство при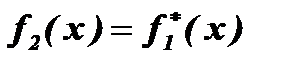 
, где 
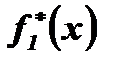- функция, комплексно-сопряжённая с f1(x).
Полагая f1(x)=U(ω), а f2(x)=H(ω) получим:
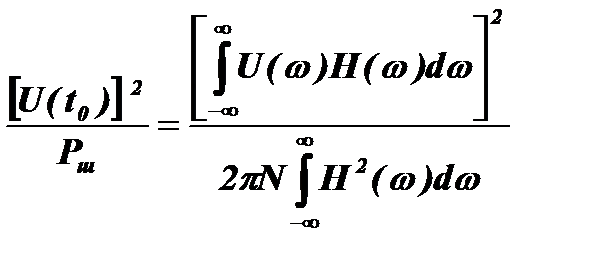
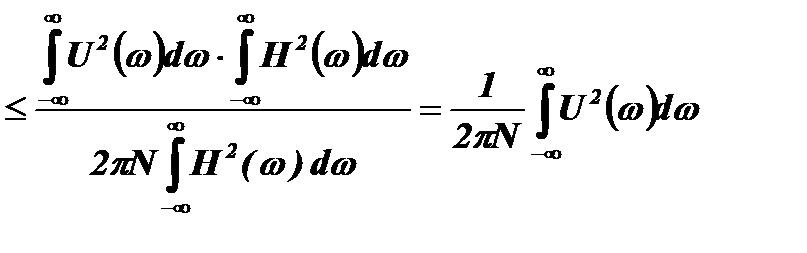
Поскольку величина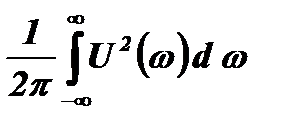 
является полной энергией сигнала Е, можно записать 
.
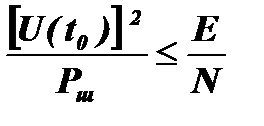Максимальное отношение сигнал/шум будет получено тогда, когда это неравенство перейдет в равенство. Для этого необходимо, чтобы H(ω)=U(ω). При выполнении этого условия отношение сигнал/шум на выходе согласованного фильтра в момент t0 будет равно отношению полной энергии сигнала к спектральной плотности мощности шума при любом виде частотной характеристики фильтра и спектра сигнала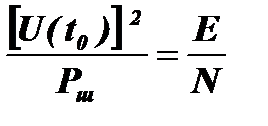 
.
Если частотная характеристика фильтра H(ω) и спектр сигнала U(ω) являются комплексно сопряженными функциями H(ω)=U*(ω), то спектральная плотность нормального шума равна N/2 Вт/Гц и максимальное отношение сигнал/шум примет более известную форму:
.
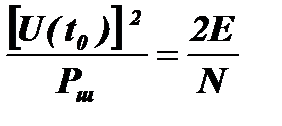Это означает, что максимум энергии сигнала выделится в фильтре в момент t0 в том случае, когда его частотная характеристика будет комплексно сопряжённой со спектром сигнала. Комплексная сопряженность частотной характеристики согласованного фильтра и спектра сигнала означает, что амплитудно-частотная характеристика согласованного фильтра должна совпадать со спектром входного сигнала и, следовательно, совпадать с амплитудно-частотной характеристикой формирующего фильтра. Фазо-частотная характеристика согласованного фильтра должна быть равна фазо-частотному спектру сигнала, взятому с обратным знаком и, следовательно, равна зеркальному отражению фазо-частотной характеристики формирующего фильтра.
При выводе отношения сигнал/шум не учитывалось усиление или ослабление сигнала при передаче его от формирующего фильтра в согласованный фильтр, а также его задержка во времени и смещение по фазе при распространении в пространстве, поскольку эти параметры не влияют не получение максимального отношения сигнал/шум на выходе согласованного фильтра.
В схеме рис. 6.5 прослеживается полная аналогия со схемой рис. 6.4, описанной в предыдущем разделе. Здесь также с одной стороны расположен источник сигнала – формирующий фильтр. Внутреннее комплексное сопротивление этого фильтра имеет активную и реактивную части, изменяющиеся в полосе его рабочих частот. Это, соответственно, амплитудно-частотная и фазо-частотная характеристики фильтра. С другой стороны имеется нагрузка (согласованный фильтр), комплексное сопротивление которой также имеет активную и реактивную части (соответственно, амплитудно-частотную и фазо-частотную характеристики). Для получения в нагрузке максимума сигнала эти две части системы должны на всех частотах спектра удовлетворять условиям равенства амплитуд (определяемых амплитудно-частотными характеристиками) и противоположности фаз (определяемых фазо-частотными характеристиками). Если спектр рассматриваемого сигнала представить в дискретном виде, то есть в виде набора отдельных частот, расположенных в его рабочей полосе, то для согласования источника и нагрузки на каждой частоте потребуется выполнение условий, приведённых в разделе 6.1.для одночастотной схемы. При объединении результатов, полученных для всех частот, мы вновь получим равенство H(ω)=U*(ω).
Таким образом, согласованная фильтрация сложных сигналов фактически определяется совпадением активных и противоположностью реактивных сопротивлений источника (формирующего фильтра) и нагрузки (согласованного фильтра).
В схеме рис. 6.5. имеются активные элементы: передатчик и приёмник, а также участок пространства, в котором рассеивается значительная часть энергии источника сигнала. Это не позволяет выявить в явном виде другую особенность взаимодействия источника и нагрузки - передачу в нагрузку только половины мощности источника. Для учета этой особенности необходимо учитывать потери в пространстве и усиление сигнала при передаче и приеме.
6.3. Согласование приёмной антенны с пространством
Теперь обратимся к случаю, когда энергия поступает в нагрузку непосредственно из открытого пространства.
Рассмотрим простую приёмную антенну в виде провода длиной l, на которую падает плоская волна электромагнитного поля с напряженностью Е. ЭДС индукции, которая наводится на антенне под влиянием этого поля, будет равна U=E×l. В результате антенна становится источником энергии для входной цепи приёмника. Мощность этого источника РПАД=UI, где I − ток в цепи антенна − входная часть приемника, определяемый общим сопротивлением этой цепи, которое состоит из сопротивления самого источника и сопротивления нагрузки. Внутренним сопротивлением этого источника энергии является сопротивление излучения антенны, имеющее активную и реактивную составляющие. Входная цепь приемника, которая является для антенны нагрузкой, также представляет собой сопротивление, имеющее как активную, так и реактивную часть. Таким образом, соединение антенны и входной цепи приёмника можно представить в виде схемы, показанной на рис.6.6.
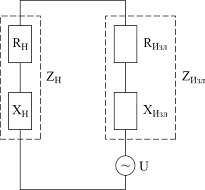
| Рис. 6.6 Схема соединения сопротивлений антенны и приемника |
Условия передачи максимальной мощности в схеме рис.6.4 получены в разделе 6.1. Используем эти условия. Тогда для согласования антенны с приемником необходимо, чтобы активные сопротивления RН и RИзл были равны, а реактивные сопротивления антенны XИзл и входной цепи приёмника XН компенсировали друг друга, то есть были равны по абсолютной величине, но имели бы разные знаки.
| Рис. 6.7 Взаимодействие диполя с падающей волной |
,
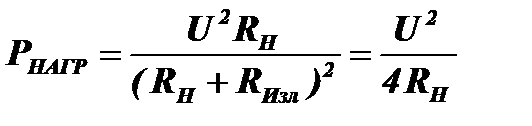а другая часть мощности
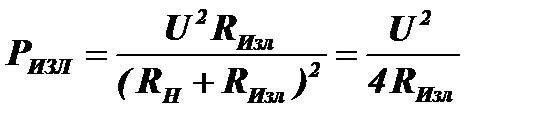
будет возвращаться в антенну. Но активным сопротивлением антенны является сопротивление излучения RИзл. Поэтому мощность РИЗЛ, выделяемая на этом сопротивлении, будет излучаться обратно в пространство и суммироваться (интерферировать) с падающей волной (рис. 6.7).
Таким образом, мы приходим к важному выводу: при согласовании антенны с приемником на его входе выделяется только половина мощности электромагнитного поля, падающего на антенну. Другая половина этой мощности выделяется в антенне. Это означает, что при согласованном приеме радиосигналов происходит излучение приемной антенны.
Эти два электромагнитных поля: падающее на антенну и излученное обратно, взаимодействуют (интерферируют) в окружающем антенну пространстве. Рассмотрим этот процесс. Мощность падающего поля равна РПАД = E×H×S, гдеS – площадь антенны, на которую падает поле.
Общая мощности РПАД, которая проходит за единицу времени через сечение антенны, делится на мощности РНАГР и РИЗЛ, которые связаны с плотностью потока энергии, падающего на антенну, и ее площадью следующими выражениями:
РНАГР = E×H×SПОГЛ; РИЗЛ = E×H×SИЗЛ;
где Е и Н – электрическая и магнитная составляющие поля,
SПОГЛ и SИЗЛ – эффективные сечения (или площади) антенны, соответствующие доле мощности, поглощаемой антенной и передаваемой в нагрузку, и доле мощности, излучаемой обратно в пространство. В общем случае эти площади могут быть не равны физической площади антенны, а также не равны между собой. Рассмотрим, от чего зависят эти площади у отрезка провода, имеющего длину l. Для антенн, обладающих поверхностью (рамка, элемент плоскости и т.д.), необходимо учитывать площадь этой поверхности.
Учитывая, что ЭДС индукции равна U=E×l, представим мощности РНАГР и РИЗЛ в виде:
; 
.
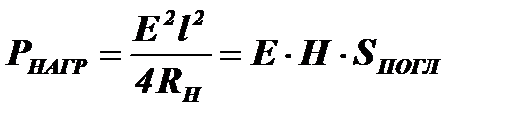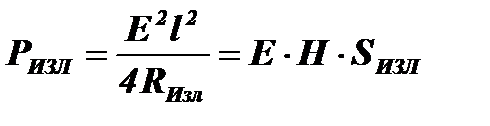Так как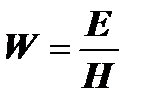 
− волновое сопротивление среды, можем записать:
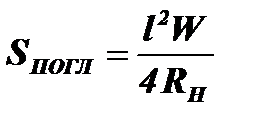; отсюда: 
.
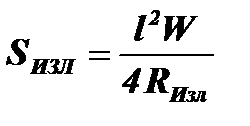Это и есть эффективные сечения провода, соответствующие поглощению электромагнитной волны и ее переизлучению. Очевидно, что при согласованной нагрузке SПОГЛ=SИЗЛ.
Теперь рассмотрим, как физически формируется эффективная площадь антенны.
| Рис. 6.8 Интерференция полей в пространстве вокруг антенны |
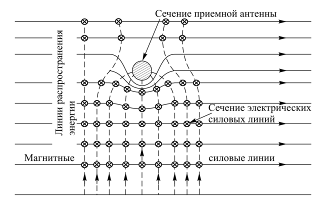Суммарное поле является суммой двух полей: падающего плоского поля и сферического поля, переизлучаемого приёмной антенной (рис.6.7). Полный поток энергии в этом случае будет выглядеть как сумма трёх составляющих: первой, образуемой плоским падающим полем; второй, возникающей от сферического поля, излучаемого диполем и третьей, являющейся результатом интерференции этих двух полей. Именно эта третья составляющая определяет эффективное сечение антенны в пространстве, которое отличается от его физического сечения и от которого зависит количество энергии "перехватываемой" антенной из падающего на нее поля. Чтобы представить себе связь интерференции указанных полей с эффективным сечением антенны, обратимся к рис.6.8.
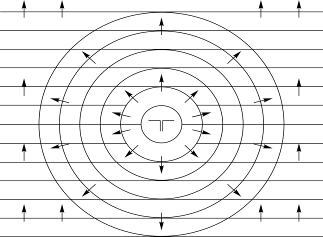
На рисунке показано сечение провода, через которое снизу вверх распространяется плоское электромагнитное поле. Слева направо проходят магнитные силовые линии этого поля. Электрические силовые линии поля направлены перпендикулярно магнитным (перпендикулярно плоскости рисунка) и их сечение изображено в виде кружочков с крестиком. Направление перемещения энергии, соответствующее направлению распространения поля, показано штриховыми линиями.
Когда магнитные силовые линии падающего поля пересекают провод, силы Лоренца вызывают в нем движение электронов, возникает электрический ток, который в свою очередь вызывает круговые (сферические, так как диполь очень мал) магнитные силовые линии вторичного поля вокруг антенны. Эти линии, складываясь с магнитными силовыми линиями падающего первичного поля, образуют суммарное поле, линии распространения которого искривляются, как показано на рисунке.
В результате искривляются и линии перемещения энергии и на провод начинают «замыкаются» не только линии, непосредственно проходящие через его сечение, но и линии, находящиеся в стороне от этого сечения. Теперь провод собирает энергию с площади, значительно превышающей это сечение. Этот эффект равносилен увеличению поверхности провода, поэтому такая площадь называется его эффективным сечением. Эффективное сечение может превышать физическое в десятки и сотни раз.
Таким образом, относительные величины мощностей, как попадающей во входную цепь приёмника, так и переизлучаемой приёмной антенной, зависят от относительных величин RН и RИзл. Меняя RН можно менять интенсивность переизлученного поля и, следовательно, изменять эффективное сечение антенны. А величина этой интенсивности и определяется интерференционной составляющей суммарного электромагнитного поля.
Дата добавления: 2016-04-19; просмотров: 2013;